
Руководство к решению задач
.pdf
21
Определить вектор напряжения в этой точке на площадке с единичным вектором нормали n€ = 14 e€1 − 34 e€2 + 34 e€3 .
Решение.
Для решения воспользуемся формулой (2.3). Умножение лучше всего выполнить в матричной форме
|
|
|
|
|
|
|
|
|
1 |
|
3 |
|
|
3 |
|
6 |
0 |
−3 |
|
|||||||
[p , p , p |
]= |
,− |
, |
|
|
0 |
5 |
|
0 |
|
= |
|||||||||||||||
|
|
|
|
|
||||||||||||||||||||||
4 |
4 |
|
|
|||||||||||||||||||||||
|
n1 |
n2 |
n3 |
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
0 |
|
4 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|||||||
|
6 |
|
9 |
,− |
15 |
,− |
3 |
|
12 |
3 |
,− |
15 |
, |
9 |
|
|
||||||||||
= |
|
|
− |
|
|
|
|
+ |
|
|
= − |
|
|
|
|
|
|
. |
||||||||
|
|
4 |
4 |
|
|
4 |
|
|
4 |
|
||||||||||||||||
|
4 |
|
4 |
|
|
|
4 |
|
|
|
|
4 |
|
|||||||||||||
Таким образом, вектор напряжения в точке М на площадке с единичным вектором n€ равен pn€ = − 14 (3e€1 +15e€2 −9e€3 ).
2.2. В точке М задан тензор напряжений |
|
|||
|
7 |
0 |
− 2 |
|
|
0 |
5 |
0 |
|
P = |
. |
|||
|
− 2 |
0 |
4 |
|
|
|
|||
Для вектора напряжений в точке М на площадке с единичным вектором
нормали n€ |
= |
2 |
e€ − |
2 |
e€ |
|
+ |
1 |
e€ |
определить: а) компоненту, перпендикулярную |
||||||||||||||||||||||||||||||||
3 |
3 |
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
1 |
|
2 |
|
|
|
3 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n€ . |
|
|
|
||||||
площадке (ее модуль), б) угол между векторами |
|
|
n€ и |
|
|
|
||||||||||||||||||||||||||||||||||||
p |
|
|
|
|||||||||||||||||||||||||||||||||||||||
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Вычислим напряжение в точке М на площадке с единичным вектором |
||||||||||||||||||||||||||||||||||||||||||
n€ по формуле (2.3) |
|
pn = n€ P , представив тензор P в девятичленной форме. |
||||||||||||||||||||||||||||||||||||||||
pn |
= |
€ |
P |
= 2 € |
|
− |
2 € |
+ |
|
1 € |
|
|
|
|
€ € |
− |
|
€ € |
+ |
|
|
€ € |
− |
€ € + |
€ € |
= |
||||||||||||||||
|
n |
|
|
e1 |
|
|
|
3 |
e2 |
|
|
3 |
e3 |
|
(7e1e1 |
|
2e1e3 |
|
|
|
5e2e2 |
|
2e3e1 |
4e3e3 ) |
|
|||||||||||||||||
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
= |
14 e€ |
− |
4 e€ |
− |
10 e€ |
|
− |
2 e€ |
+ |
4 e€ |
= |
4e€ − |
10 e€ . |
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
3 |
|
|
1 |
|
|
3 |
3 |
|
|
3 |
2 |
|
|
3 |
1 |
|
|
3 |
3 |
|
|
|
1 |
3 |
2 |
|
|
||||||||
Таким образом, |
|
|
|
|
= 4e€ |
|
− |
10 |
e€ . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
p |
n€ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
3 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Численное значение компоненты вектора |
|
|
|
|
n€ , перпендикулярной пло- |
|||||||||||||||||||||||||||||||||||||
|
|
|
p |
|||||||||||||||||||||||||||||||||||||||
щадке, вычислим по формуле pnn |
= |
|
n€ n€ . |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||

|
|
|
|
|
|
|
|
|
|
|
|
|
22 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
2 |
|
|
|
2 |
|
|
1 |
|
|
|
8 |
|
20 |
|
44 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
p |
nn |
= p |
|
n€ = |
4e€ − |
|
|
|
|
e€ |
|
|
|
e€ |
− |
|
e€ |
+ |
|
|
e€ |
= |
|
+ |
|
= |
|
|
|
|
. |
|
|
|||
|
3 |
|
|
3 |
3 |
3 |
9 |
9 |
||||||||||||||||||||||||||||
|
|
|
n€ |
|
1 |
|
2 |
|
|
3 1 |
|
|
2 |
|
3 |
|
|
|
|
|
|
|
||||||||||||||
Угол между векторами |
|
|
|
и |
|
n€ следует из условия pn n€ = |
|
|
|
n€ |
|
cos θ, |
||||||||||||||||||||||||
|
p |
n€ |
|
|
p |
|
||||||||||||||||||||||||||||||
откуда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos θ = |
pn€ n = |
|
|
44 / 9 |
|
|
|
≈ 0,94 |
и θ = 20o . |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
pn |
|
|
|
|
|
|
|
10 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
€ |
|
|
|
|
42 + |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2.3. Напряженное состояние в любой точке сплошной среды в декартовой системе координат задано тензором
P = 3x x |
2 |
e€ e€ |
+ 5x2 e€ e€ |
+ 5x2 e€ |
e€ + 2x |
3 |
e€ |
e€ |
+ 2x |
3 |
e€ e€ . |
|||||
1 |
1 |
1 |
2 |
1 |
2 |
2 |
2 |
1 |
2 |
3 |
|
3 |
2 |
|||
Определить вектор напряжения в точке М (2, 1, |
3) на площадке, касатель- |
|||||||||||||||
ной в этой точке к цилиндрической поверхности x22 + x32 = 4 (рис. 2.1).
Решение.
Компоненты напряжения в точ- |
|
|
|
|
|
|
|
|
|
||||||||||||
ке М принимают значения, которые |
|
|
|
|
|
|
|
|
|
||||||||||||
удобно обозначить таблицей |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
6 |
5 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P = |
|
5 |
0 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
3 . |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
0 2 3 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Единичный |
вектор |
|
нормали |
в |
|
|
|
|
|
|
|
|
|
||||||||
точке М |
определяется |
вектором |
|
|
|
|
|
|
|
|
|
||||||||||
gradϕ = |
|
(x22 + x32 − 4) и, следователь- |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
Рис. 2.1 |
|
|
|
|||||||||||||
но, в точке М |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
ϕ = 2x2e€2 + 2x3e€3 = 2e€2 + 2 3e€3 . |
|
|
|
|
|||||||||||
Тогда единичный вектор нормали в точке М есть n€ = 1 e€ |
+ |
3 e€ . |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
2 |
3 |
Наконец, вектор напряжения на площадке, перпендикулярной к n€ в |
|||||||||||||||||||||
точке М, равен |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
6 |
5 |
0 |
|
|
0 |
|
|
|
|
|
|
5 |
|
|
|
|
|
||
|
|
|
0 |
2 |
3 |
|
|
|
5 |
/ 2 |
или P |
= |
e€1 +3e€2 |
+ |
|
3e€3 . |
|
||||
|
|
5 |
|
|
1/ 2 |
= |
|
3 |
|
2 |
|
|
|||||||||
|
|
|
|
|
|
|
|
3 / 2 |
|
|
3 |
|
n |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
0 2 3 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||

23
2.4. Напряженное состояние в некоторой точке задано в декартовой системе координат Ox1 x2 x3 тензором
|
|
|
2 |
|
-2 |
0 |
|
|
P = |
|
− 2 |
|
2 |
|
|
|
|
|
0 . |
|
|||
|
|
|
0 |
|
0 - |
|
|
|
|
|
|
2 |
|
||
Определить тензор напряжений P′ |
для повернутых осей Ox1′x2′ x3′, кото- |
||||||
рые связаны с осями без штрихов тензором преобразования |
|||||||
|
|
0 |
|
1/ |
2 |
1/ 2 |
|
|
|
|
|
||||
A = |
1/ 2 |
1/ 2 |
-1/ 2 |
. |
|||
|
−1/ |
|
2 1/ 2 |
-1/ 2 |
|
||
|
|
|
|||||
|
|
|
|
|
|
|
|
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Для |
|
решения |
применим |
|
закон |
преобразования |
напряжений в |
виде |
|||||||||
pij′ = aip a jq p pq |
или P′ = A P AC . Вычисление лучше произвести умножени- |
||||||||||||||||
ем матриц. Таким образом, |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
0 |
1/ |
2 1/ |
2 |
|
|
2 -2 0 |
0 |
|
1/ 2 -1/ |
2 |
|
|
|||
[pij′ ]= |
|
1/ |
2 1/ 2 |
-1/ 2 |
|
|
|
|
1 / |
2 |
1/ 2 |
1/ 2 |
|
|
= |
||
|
|
− 2 |
2 0 |
|
|
||||||||||||
|
|
|
2 1/ 2 |
|
|
|
|
|
|
1 / |
2 -1/ 2 |
-1/ 2 |
|
|
|||
|
−1 / |
-1/ 2 |
0 0 - 2 |
|
|
|
|||||||||||
|
|
|
|
|
|
|
0 |
0 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
0 |
1- |
2 -1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
2 |
-1 |
1+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|||
2.5. Считая атмосферный воздух совершенным газом, температура которого меняется линейно с высотой T = T0 −αx3 , где T0 – температура на
уровне Земли, а координата x3 отсчитывается от уровня Земли вверх. Определить атмосферное давление как функцию x3 в условиях гидростатики.
Решение.
В этом случае из уравнения состояния следует ( p = сRT )
p = сR(T0 −αx3 ). |
(1) |
Так как из массовых сил действует только сила тяжести, то f3 = −g и уравнение гидростатического равновесия дает
dp |
= −сg . |
(2) |
|
||
dx3 |
|
|
24
Подставляя значение с из (1), будем иметь |
|
|
|
|
|
|||||||||
|
dp |
|
= − |
|
|
pg |
|
|
|
. |
(3) |
|||
|
dx |
3 |
|
(T |
−αx |
3 |
)R |
|||||||
|
|
|
|
|
|
|
0 |
|
|
|
|
|
||
Разделяем переменные и интегрируем: |
|
|
|
|
|
|
|
|||||||
ln p = |
|
|
g |
ln(T |
−αx |
3 |
)+ln C , |
(4) |
||||||
|
|
|
||||||||||||
|
|
αR |
0 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
||||||
где С – постоянная интегрирования.
После потенцирования уравнение (4) примет следующий вид
p = C(T0 −αx3 ) |
g |
|
||||
|
. |
(5) |
||||
αR |
||||||
Постоянную С определим из условия при x3 = 0 , |
p = p0 , где p0 – давление |
|||||
на поверхности Земли и |
|
|
|
|
|
|
C = p T − |
g |
|
||||
|
. |
|
||||
αR |
|
|||||
0 |
0 |
|
|
|
|
|
Подставляя это значение в (5) и сделав простые преобразования, получим зависимость
|
|
αx3 |
|
g |
|
|
|
Rα |
|
||||
|
− |
|
(6) |
|||
T |
||||||
p = p0 1 |
|
|||||
|
|
0 |
|
|
||
атмосферного давления воздуха от высоты над поверхностью Земли.
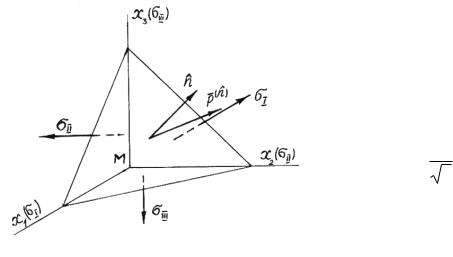
2.6. Главные напряжения в точке М таковы: σI =12 , σII = 3 , σIII = −6 .
Определить вектор напряжения и его нормальную компоненту на октаэдрической площадке в точке М.
Решение.
Октаэдрической называется площадка, которая составляет равные углы с главными направлениями (рис. 2.2). Нормаль к октаэдрической площадке в главных осях дается выражением
n€ = 13 (e€1 + e€2 + e€3 ).
Тогда, согласно формулы (2.3), вектор напряжения на такой площадке равен
Рис. 2.2

25
|
|
|
= |
1 |
(e€ |
|
+ e€ + e€ |
) (σ e€ e€ |
+ σ |
|
e€ e€ |
|
+ σ |
e€ e€ )= |
1 |
|
(12e€ |
+3e€ |
−6e€ ), |
|||||||||||||||
|
p |
|
|
|
|
|||||||||||||||||||||||||||||
|
|
n |
|
3 |
1 |
2 |
|
3 |
|
|
I 1 |
1 |
|
|
II |
2 2 |
|
III |
3 |
|
3 |
3 |
|
1 |
2 |
3 |
||||||||
а его нормальная компонента согласно формулы (2.9) |
|
1 |
|
|
|
|
||||||||||||||||||||||||||||
|
|
N = n€ |
|
|
|
= 1 |
(e€ |
+ e€ |
|
+ e€ |
) |
1 |
(12e€ |
+3e€ |
− |
6e€ |
)= |
|
(12 +3 −6)= 3 . |
|||||||||||||||
|
|
p |
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
3 |
3 |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
n |
3 |
|
1 |
2 |
|
3 |
|
|
|
|
|
1 |
2 |
|
|
3 |
|
|
|
|
||||||
|
|
2.7. Поле напряжений в сплошной среде задано тензором |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x2 x |
2 |
|
|
|
|
(1− x2 )x |
|
|
|
0 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σ |
ij |
= |
(1− x |
2 )x |
|
|
1 |
(x3 − |
3x |
2 |
) |
|
0 |
|
|
|
. |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1 |
|
3 |
|
2 |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2x3 |
|
|
|
||||||||
Определить: а) распределение массовых сил, если уравнения равновесия удовлетворяются повсюду; б) величины главных напряжений в точке
М(а,0, 2 a ); максимальное касательное напряжение в точке М; главные значения девиатора напряжения в точке М.
Решение.
а) Воспользуемся формулами (2.5) для записи уравнений равновесия
2x1 x2 − 2x1 x2 +ρf1 = 0,
1− x22 + x22 −1+ρf2 = 0 , 4x3 +ρf3 = 0.
Из решения этой системы следует, что f3 = − 4ρx3 .
б) Чтобы найти величины главных напряжений в точке М, запишем тензор напряжений для этой точки
|
|
|
|
|
0 |
a |
0 |
|
|
|
|
|
|
|
0 |
0 |
|
|
|
|
|
|
a |
|
||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
0 |
8a |
||
и вычислим главные напряжения с помощью определителя |
||||||||
|
− σ |
a |
0 |
|
= −σ[− σ(8a − σ)]+ a[− a(8a − σ)]= (8a − σ)(σ2 − a2 )= 0, |
|||
|
|
|||||||
|
a − σ 0 |
|
||||||
|
0 |
0 |
8a −σ |
|
|
|
|
|
откуда следует: σI |
= 8a , σII = a , σIII |
= −a . |
|
|||||
в) Для вычисления максимального касательного напряжения применим формулу

26
σS = 12 (σIII − σI )= 12 (− a −8a)= − 4,5a .
г) Главные значения девиатора напряжений найдем с помощью определителя
|
− |
|
8 |
a − s |
|
|
a |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
3 |
|
|
|
8 |
|
|
|
|
|
|
|
|
16 |
|
|
16 |
|
|
55 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
a |
− |
|
|
|
a − s |
0 |
|
= |
|
|
a − s s2 |
+ |
|
|
|
as + |
|
a2 = 0 , |
||||||||
|
|
3 |
|
3 |
|
9 |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
16 |
|
|
3 |
|
|
|
|
|
||||||||
|
|
0 |
|
|
|
|
0 |
|
|
|
|
|
a − s |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
откуда sI |
|
= |
16 |
a , |
sII |
|
= − |
5 |
a , |
|
sIII = − |
1 |
a . |
|
|
|
|
|
|
|
|
|||||||
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
3 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|||||
Из данного примера видно, что характеристическое уравнение для тен- |
||||||||||||||||||||||||||||
зора напряжений |
|
|
представляет |
собой |
кубическое |
уравнение вида |
||||||||||||||||||||||
s3 + ps + q = 0 .
Для проверки правильности ответов воспользуемся формулой (2.12)
sI = σI −σM |
= 8a − |
|
8 |
a = |
16 |
|
a , |
||||||
|
|
|
|
3 |
|
||||||||
|
|
|
3 |
|
|
|
|
|
|||||
sII = σII −σM |
= a − |
8 |
a = − |
5 |
a , |
||||||||
|
|
|
|
||||||||||
|
|
3 |
|
|
3 |
|
|
||||||
sIII = σIII −σM |
= −a − |
|
8 |
a = − |
11 |
a , |
|||||||
|
|
|
|||||||||||
|
|
|
3 |
3 |
|
||||||||
где σM = 13 I1 = 13 σii .
Задачи для самостоятельного решения
2.8. В точке М задан тензор напряжений |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
7 |
−5 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
−5 |
3 |
1 |
|
|
|
|
|
|
|
|
|
|
|
P = |
. |
|||||
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
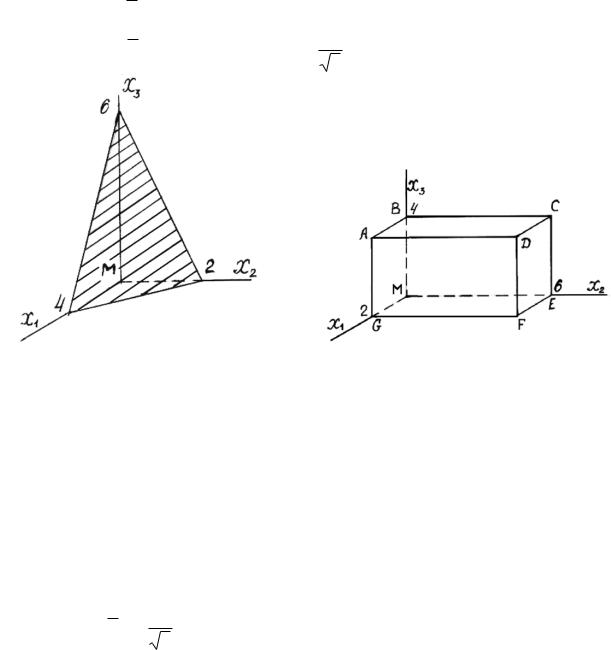
Определить вектор напряжения на площадке, проходящей через точку |
|||||||||||||||
М параллельно плоскости АВС (рис. 2.3). |
|
|
|||||||||||||
Ответ: |
|
|
= − |
9 |
e€ |
+ |
5 |
e€ |
+ |
10 |
e€ . |
|
|
|
|
p |
n€ |
|
|
|
|||||||||||
|
|
|
|
|
|
||||||||||
|
|
7 |
1 |
7 |
2 |
7 |
|
3 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
||||||
27
2.9. В точке М дан тензор напряжений
|
14 |
7 |
−7 |
|
|
7 |
21 |
0 |
|
P = |
. |
|||
|
−7 |
0 |
35 |
|
|
|
Определить вектор напряжения в точке М на площадке, параллельной плоскости: а) BGE, б) BGFC в элементарном параллелепипеде, изображенном на рис. 2.4.
Ответ: а) pn€ =11e€1 +12e€2 +9e€3 ;
б) pn€ = (21e€1 +14e€2 +12e€3 ) 15 .
С
|
B |
A |
|
Рис. 2.3 |
Рис. 2.4 |
2.10. Определить нормальную и касательную компоненты напряжения
на плоскости BGFC задачи |
2.9. |
|
||||
Ответ: σn = |
63 |
|
, στ = |
|
37,5 |
. |
|
5 |
|||||
5 |
|
|
|
|||
2.11. Главные |
напряжения в точке М таковы: σI =12 , σII = 3 , |
|||||
σIII = −6 . |
|
|
|
|
||
Определить вектор напряжения и его касательную компоненту на октаэдрической площадке в точке М.
Ответ: pn€ = 13 (12e€1 +3e€2 −6e€3 ), σn = 3.
2.12. Определить величины главных напряжений для тензоров
|
|
|
|
|
|
28 |
|
|
|
|
|
|
|
|
|
|
0 |
1 |
1 |
|
|
|
|
2 |
1 |
1 |
|
а) |
P1 |
|
1 |
0 |
1 |
|
и б) |
P2 |
|
1 |
2 1 |
|
|
= |
|
= |
|
||||||||||
|
|
|
1 |
1 |
0 |
|
|
|
|
1 |
1 |
2 |
|
|
|
|
|
|
|
|
|
||||||
и показать, что главные оси этих тензоров совпадают.
Ответ: а) σI = 2 , σII = σIII = −1; б) σI = 4 , σII = σIII =1.
2.13. Разложить тензор напряжений
|
3 |
−10 |
0 |
|
|
−10 |
0 |
30 |
|
P = |
|
|||
|
0 |
30 |
− 27 |
|
|
|
на шаровую часть и девиатор и найти главные значения девиатора напряжений.
Ответ: sI = 31, sII = 8 , sIII = −39 .
2.14.Показать, что нормальная компонента вектора напряжения на октаэдрической площадке равна одной трети первого инварианта тензора напряжений.
2.15.В некоторой точке задан тензор напряжений
|
0 |
1 |
2 |
|
|
|
1 |
σ22 |
1 |
|
|
P = |
|
, |
|||
|
2 |
1 |
0 |
|
|
|
|
|
причем величина σ22 не указана. Определить σ22 так, чтобы вектор напря-
жения на некоторой площадке в этой точке обращался в нуль. Найти единичную нормаль к этой свободной от напряжений площадке.
Ответ: σ |
|
= 1, |
|
= |
1 |
(e€ |
− 2e€ |
+ e€ ). |
|
n |
|||||||
|
22 |
|
|
|
6 |
1 |
2 |
3 |
29
Раздел 3
Кинематика сплошной среды
Если pij... – любое скалярное, векторное или тензорное свойство континуума дано в лангранжевом представлении
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
pij... |
= pij... ( |
|
|
|
|
|
,t), |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
то индивидуальная производная по времени от этой величины имеет вид |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dpij... |
|
|
|
|
|
|
|
∂pij... ( |
|
|
|
|
|
,t) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3.1) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
∂t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Если некоторое свойство задано функцией pij... в эйлеровых переменных |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
pij... |
|
= pij... ( |
|
|
,t), |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
то вычисление производной приводит к выражению |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
dpij... ( |
|
,t) |
|
|
|
|
|
∂pij... ( |
|
|
,t) |
|
|
|
|
|
|
|
∂pij... ( |
|
|
,t) |
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
r |
= |
r |
+ |
r |
|
k |
, |
|
|
|
|
|
|
|
|
|
(3.2) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
∂t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂xk |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|||||||||||||||||||||||||||||||||
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
dpij... ( |
|
,t) |
|
|
|
|
∂pij... ( |
|
|
|
,t) |
|
|
|
|
|
|
|
|
|
|
∂pij... ( |
|
|
|
,t) |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
r |
|
|
|
|
r |
+ vk |
r |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
(3.3) |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂t |
|
|
|
|
|
|
|
|
|
∂xk |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= ui ( |
|
,t), |
|||||||||||||||||||||||||||
Если поле перемещений дано в лагранжевых переменных ui |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
X |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
то |
|
|
|
|
|
|
|
|
|
|
|
|
|
dui ( |
|
|
|
|
|
,t) |
|
|
|
|
|
|
|
|
∂ui ( |
|
|
|
|
|
|
,t) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
vi = u&i |
X |
X |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3.4) |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
o |
|
|
|
|
|
d |
|
|
|
( |
|
|
|
|
|
|
|
,t) |
|
|
|
|
|
|
|
|
∂ |
|
(X ,t) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
u |
X |
|
|
|
|
|
|
|
|
u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
V = u |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
∂t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
Если перемещение задано в эйлеровой форме ui |
|
|
= ui ( |
|
|
,t ) , то |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
r |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
• |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂ui |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
du( r,t ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂ui ( r,t ) |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
vi ( |
|
,t ) ≡ ui ( |
|
,t ) ≡ |
= |
|
|
|
+ vk ( |
|
|
,t ) |
, |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
r |
r |
|
|
r |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂xk |
(3.5) |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
• |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
du( r,t ) |
= ∂u( r,t ) + |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
( |
|
,t ) ≡ |
|
i ( |
|
,t ) |
= |
|
( |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
V |
r |
u |
r |
V |
r |
,t ) |
u( r,t ). |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Если скорость дана в лагранжевой форме, то
30
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
• |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dvi ( X ,t ) |
|
= ∂vi ( X ,t ) , |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
ai ≡ vi ≡ |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3.6) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
• |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a ≡ |
|
|
|
|
≡ |
dV i |
( X ,t ) |
|
= ∂V( X ,t ) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
V |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Если же скорость выражена в эйлеровой форме, то |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
d |
|
|
|
i ( |
|
|
|
,t ) |
|
|
|
|
|
∂vi ( |
|
|
,t ) |
+ vk ( |
|
,t ) |
∂vi ( |
|
|
|
,t ) |
, |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ai ( |
|
|
,t ) ≡ |
v |
r |
= |
|
r |
r |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
r |
r |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂xk |
|
|
|
|
|
|
||||||||||||||||||||||||||
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3.7) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
,t ) |
|
|
|
= ∂ |
|
|
( |
|
|
|
|
|
,t ) + |
|
|
|
|
( |
|
|
|
,t ) |
|
|
|
|
|
|
( |
|
|
,t ). |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
a( |
|
|
,t ) ≡ |
dV |
r |
|
|
|
V |
r |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
r |
|
|
|
V |
r |
|
V |
r |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Дифференциальные уравнения линий тока имеют вид |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx1 |
= |
|
dx2 |
|
= |
dx3 |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3.8) |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v |
|
|
|
|
|
|
|
|
|
|
|
|
v |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Тензор градиента скорости |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂v1 |
|
|
|
|
|
|
|
|
|
|
|
∂v1 |
|
|
|
|
|
|
|
|
|
|
∂v1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂x1 |
|
|
|
|
|
∂x2 |
|
|
|
|
|
|
|
∂x3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂v |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
Y = |
|
|
i |
|
|
|
|
|
|
|
|
|
|
∂v |
2 |
|
|
|
|
|
|
|
|
|
|
|
∂v |
2 |
|
|
|
|
|
|
|
|
|
|
∂v |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3.9) |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
∂x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂x |
|
|
|
|
|
|
|
|
|
|
∂x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j |
|
|
|
|
|
|
|
|
∂x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂v3 |
|
|
|
|
|
|
∂v3 |
|
|
|
|
|
|
|
|
|
∂v3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂x |
2 |
|
|
|
|
|
|
|
|
|
|
∂x |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
который можно разложить на симметричную и антисимметричную части |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
∂v |
i |
|
|
1 |
|
|
|
∂v |
i |
|
|
|
|
|
|
|
|
∂v j |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
∂v |
i |
|
|
|
|
|
|
|
|
|
|
∂v j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
Y ≡ |
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
= D |
+V |
, |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ij |
∂xi |
|
2 |
|
|
∂x j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
∂x j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ij |
|
|
|
|
ij |
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
∂xi |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂xi |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3.10) |
|
|
|
|
Y = |
1 |
( |
|
|
|
|
+ |
|
|
|
) |
+ |
1 |
( |
|
|
|
− |
|
|
|
)= D +V . |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
V |
|
|
V |
V |
|
|
V |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Тензор скоростей деформаций (симметричная часть тензора Y ) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
∂vi |
|
|
|
|
|
|
|
∂v j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
D |
≡ D |
ji |
= |
|
|
|
|
|
|
|
+ |
|
|
|
|
, или D = |
(V + V ). |
(3.11) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ij |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
∂x j |
|
|
|
|
|
|
|
∂xi |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
Тензор завихренности (антисимметричная часть тензора Y )
