Руководство к решению задач

11

D = 12 ( D + Dc ) + 12 ( D − Dc ) = E + F ,

где Е = Ес – симметричная часть тензора D, F = -Fc – антисимметричная часть тензора D.

Вычислим их значения

−3e€1e€2 −3e€1e€3 + 3e€2e€1 − e€2e€3 +3e€3e€1 + e€3e€2 =

=3e€1e€1 + 4e€1e€3 + 6e€2e€1 + 7e€2e€2 +10e€3e€1 + 2e€3e€2 = D .

1.5.В трехмерном пространстве расшифровать следующие тензорные

символы: Aii, Bijj, Rij, aiTij, aibjSij.

Решение.

Aii представляет одну сумму:

Aii = A11 + A22 + A33 .

Выражение Bijj представляет три суммы:

1)при i = 1 B111 + B122 + B133 ,

2)при i = 2 B211 + B222 + B233 ,

3)при i = 3 B311 + B322 + B333 .

Выражение Rij представляет девять компонент, которые можно записать в виде матрицы

Выражение aiTij представляет три суммы:

14

Поэтому

а) Dij xi x j = D11(x1 )2 + D22 (x2 )2 + D33 (x3 )2 + 2D12 (x1x2 )+ 2D13 (x1x3 )+ 2D23 (x2 x3 ).

б) Dij xi x j = 0, т.к. D11 = −D11 , D12 = −D21 и т.д.

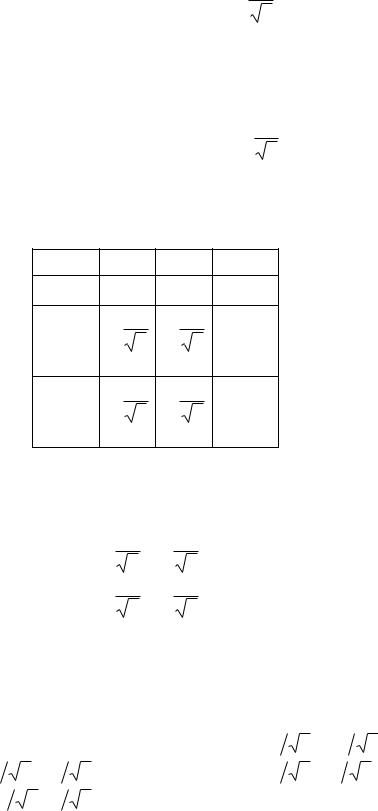
1.10. Оси декартовой системы координат Ox1′x2′ x3 получены поворотом системы Ox1 x2 x3 на угол θ вокруг оси x3 . Определить коэффициенты преобразования aij указанных осей и найти компоненты вектора v = v1e€1 + v2e€2 + v3e€3 в

системесоштрихами.

Решение.

По определению aij = cos(xi′,x j ).

Углы между соответствующими осями указаны на рис. (1.3), что позволяет найти таблицу направляющих косинусов:

Таким образом, тензор преобразования имеет вид

v3′ = a3 j v j = v3 .

1.11. Пусть углы между направлениями осей координат системы со штрихами и системы без штрихов даны в следующей таблице:

Определить коэффициенты преобразования aij и показать, что выполнены условия ортогональности.

15

Решение.

Коэффициенты aij являются направляющими косинусами и могут быть сразу вычислены в соответствии с данной таблицей углов. Таким образом,

ний соответствующих элементов второго и третьего столбцов; 3) сумма произведений соответствующих элементов любых двух столбцов

должна быть равна нулю; сумма квадратов элементов любого столбца должна быть равна единице.

Если условие ортогональности записано в форме a ji aki = δjk , то вместо

столбцов перемножаются строки.

Указанное выше решение удовлетворяет всем этим требованиям.

произведение a D , D b и a D b .

Решение.

Пусть a D = v ; тогда

16

1.14. Найти главные направления и главные значения декартова тензора Т второго порядка, который представлен матрицей

Решение.

Для определения главных значений имеем определитель

Пусть теперь ni(1) – компоненты единичного вектора главного направления, соответствующего λ(1) =1. Тогда имеем следующую систему уравнений:

n3(1) = ±1.

17

Для λ(2) = 2 система запишется в виде

Ориентация главных осей xi относительно исходной системы xi определяется направляющими косинусами, которые даны в следующей таблице:

Отсюда видно, что матрица тензора преобразования такова:

Задачи для самостоятельного решения

1.16.Для произвольных векторов a и b показать, что

λ=( a ×b ) ( a ×b ) +( a b )2 =( ab )2 .

••

1.17.Пусть u = ω×u и v = ω×v ; показать, что

ddt ( u ×v ) = ω×( u ×v ) .

Определить главные значения и направления главных осей.

а) Показать, что выполнены условия ортогональности.

б) Определить в системе со штрихами координаты точки, имеющие ра-

19

Раздел 2

Равновесие сплошной среды

ОсновноезначениевравновесиисплошнойсредыимеютравенстваКоши.

Векторы напряжений p1 , p2 , p3 , приложенные к координатным пло-

щадкам, не имеют объективного физического смысла, так как зависят от выбора системы координат.

Проекция равенства (2.1) на оси координат дает три равенства:

В этих равенствах первый индекс при р отмечает принадлежность напряжения к площадке, перпендикулярной к данной оси координат, второй – ось проекций. Они позволяют вычислить напряжение pn на любой площадке,

если известна ее ориентация n€ .

Если использовать операции умножения тензора на вектор справа или

где P – тензор напряжений,

ρ – плотность сплошной среды,

f– объемная (массовая) сила.

Впроекциях на декартовы координатные оси (2.4) приводится к системе трех дифференциальных уравнений в частных производных относительно компонент тензора напряжений.