методичка 2 курс 3 семестр3 1911

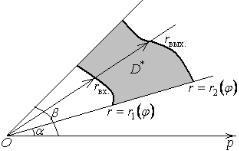
r2

f x;y dxdy f r cos ; r sin r dr d d

f r cos ; r sin r dr

D

D*

r1

Приложения двойного интеграла

1.

Площадь плоской фигуры, ограниченной областью

D ,

находится по

формуле

S dxdy ,

D

или, в полярных координатах

S rdr d .

D

2.

Объем

цилиндрического

тела, ограниченного сверху

непрерывной

поверхностью

z f2 x; y , снизу непрерывной поверхностью

z f1 x; y и сбоку

цилиндрической поверхностью,

вырезающей на

плоскости

xOy область D ,

D

В частности, если тело ограничено сверху непрерывной поверхностью

z f x; y , снизу плоскостью z 0

и сбоку цилиндрической поверхностью,

вырезающей на плоскости xOy область D ,

то

его объем вычисляется

по

формуле

f x; y dxdy .

V

D

3.

Масса плоской пластинки, занимающей область D плоскости xOy

и

имеющей переменную плотность x; y , вычисляется по формуле

m x; y dxdy .

D

Тройной интеграл

f x;y; z dxdydz

n

lim

f xi ; yi ; zi Vi

n

V

max di 0 i 1

Вычисление тройного интеграла в декартовых координатах

b

2

x

z2 x; y

f x;y; z dxdydz dx dy

f

x;y; z dz

V

a

1

x

z1 x; y

f x;y; z dxdydz

f r cos ;r sin ; z r dr d dz

V

V *

r2

z2

r;

d

rdr

f r cos ;r sin ; z dz .

r1

z1 r;

f (x; y; z)dxdydz

f ( cos sin ; sin sin ; cos ) sin 2d d d

V

V *

2

2

2 ( , )

d sin d

f ( cos sin ; sin sin ; cos ) 2d.

1

1

1 ( , )

V dxdydz ,

V

или, в цилиндрических координатах

V rdrd dz .

V

2.

Масса тела V , имеющего переменную плотность x; y; z ,

f x; y; z dl lim

n

xˆi ; yˆi ; zˆi li

f

AB

n

i 1

0

Вычисление криволинейного интеграла I рода

1.

Кривая задана параметрическими уравнениями

Если кривая AB задана параметрическими уравнениями

x x t ,

y t ,

y

z t ,

z

где параметр t ; ,

а

x t ,

y t

и

z t

– непрерывно дифференцируемые

функции от параметра t ,

причем точке A соответствует

t ,

точке B

–

значение t , то

f x; y; z dl f x t ; y t ; z t

xt 2 yt 2 zt 2 dt .

AB

2.

Кривая задана явным уравнением

x a;b , где x –

Если плоская кривая AB задана явным уравнением y x ,

непрерывно дифференцируемая функция, то

f x; y dl b f x; x

dx .

1 y 2

x

AB

a

3.

Кривая задана полярным уравнением

r r ,

Если

плоская кривая

AB задана

явным

уравнением

в

полярных координатах, то

f x; y dl

f r cos ;r sin r 2 r 2

d .

AB

R x; y; z dz lim

n

R xˆi ; yˆi ; zˆi zi ,

n

AB

0 i 1

Сумму криволинейных интегралов

P x, y, z dx,

Q x, y, z dy,

R x, y, z dz

AB

AB

AB

P x; y dx Q x; y dy P x t ; y t x t dx Q x t ; y t y t dt .

AB

2.

Кривая задана явным уравнением

x a;b ,

где x

Если плоская кривая AB задана явным уравнением y x ,

–

непрерывно-дифференцируемая функция, а функции

P x; y и

Q x; y

AB

a

P x; y dx Q x; y dy

Q

P

x

y

dxdy

L

D

Работа переменной силы F P x; y; z i Q x; y; z j R x; y; z k ,

производящей работу на криволинейном участке AB , находится по формуле

A P x; y; z dx Q x; y; z dy R x; y; z dz .

AB

Поверхностный интеграл I рода

n

f x;y; z ds lim f xi ; yi ; zi Si

n

S

max di 0 i 1

Вычисление поверхностного интеграла I рода

f x;y; z ds f x;y; z x; y

dxdy

1

zx

z y

2

2

S

D

где z z x; y – уравнение поверхности S

Поверхностный интеграл II рода

n

xi ; yi ; zi

i

f

x;y; z dxdy lim f

0

S

n i 1

Общим видом поверхностного интеграла II рода служит интеграл

P x; y; z dydz Q x; y; z dxdz R x; y; z dxdy Pdydz Qdxdz Rdxdy ,

S

S

S

S

U

U

cos

U

cos

U

cos ,

x

y

z

M

M

M

M

где cos

y

cos

, cos

x

,

z

– направляющие косинусы вектора ,

Величина производной

по направлению

U

показывает

мгновенную

M

скорость поля в точке М. Если производная по направлению

U

0 , то поле

U

0 ,

M

в направлении вектора возрастает, если

то поле в направлении

M

вектора убывает.

Вектор, координатами которого являются значения частных производных

функции (скалярного поля)

U U x; y; z

в

точке

M x; y; z , называют

U

U

U

gradU

;

;

.

M

x

y

z

M

M

M

П P cos Q cos R cos ds

или П Pdydz Qdxdz Rdxdy

S

S

Физический смысл потока. Величина П равна объему жидкости,

которая протекает через поверхность S

за единицу времени (независимо от

физического смысла поля).

производных компонент

векторного поля

P

Q

R

и

обозначается

x

y

z

M , т. е.

символом divF

M P

Q

R .

divF

x

y

z

Физический смысл дивергенции. Дивергенция

характеризует

распределение и интенсивность источников и стоков поля.

Поток через замкнутую поверхность S , ограничивающую некоторый

объем V , можно вычислить:

П Pdydz Qdxdz Rdxdy div

dxdydz

-

формула

Остроградского-

F

S

V

Гаусса.

В этом случае за направление вектора n

обычно берут

направление

внешней нормали и говорят о потоке изнутри поверхности S .

Если векторное поле

M есть поле скоростей текущей жидкости, то

F

величина потока П через замкнутую

поверхность

дает

разность между

i

j

k

R

Q

P

R

Q

P

rot F M

i

j

k .

x

y

z

y

z

x

x

z

y

P

Q

R

Ц F d r

rot F n dS – формула Стокса.

L

S

Формула показывает, что циркуляция вектора

F вдоль

замкнутого

через поверхность S ,

контура L равна потоку ротора этого вектора F

и ограниченную контуром L (натянутую на

лежащую в поле вектора F

контур).

M 0 , векторное поле

Если divF

- соленоидальное (или трубчатое)

F

M

Если rot

F

0

, векторное поле F - потенциальное (или безвихревое).

Тогда можно вычислить потенциал поля.

x

y

z

U x; y; z P x; y0 ; z0 dx Q x; y; z0 dy R x; y; z dz

x0

y0

z0

M 0

M

Если divF

и rot

F

0

, векторное поле F - гармоническое.

4.5. Ряды

Сумма членов бесконечной

числовой

последовательности

u1 ,u2 ,...,un ,...

называется числовым рядом: u1 u2 ... un

... un

n 1

Сумма ряда S lim Sn , где Sn u1 ... un

n

Эталонные ряды

название

вид

сходится

расходится

Геометрическая

q n

q

1

q

1

прогрессия (ГП)

n 1

Обобщенный

гармонический ряд

1

s 1

s 1

s

(ОГР)

n 1 n

Название

Признак

Применение

Для всех рядов

Необходимы

й (НП)

если lim un 0

- ряд un может сходиться,

n

n 1

а может и расходиться

если lim un 0

- ряд un расходится

n

n 1

Знакоположительные числовые ряды un

n 1

Первый

Если к ряду (1)

признак

Пусть даны два ряда

un (1) и

vn

(2).

удобно подобрать

n 1

n 1

сравнения

Если выполняется неравенство

un vn (3),

эталонный ряд (2),

(I ПР)

удовлетворяющий

то

неравенству (3)

из сходимости ряда (2) следует

сходимость ряда (1);

из расходимости ряда (1) следует

расходимость ряда (2).

Второй

Если к ряду (1)

Пусть даны два ряда

un (1) и

vn

(2).

признак

удобно подобрать

n 1

n 1

сравнения

Если существует конечный и отличный от

эталонный ряд (2).

(II ПР)

Но неравенство (3)

un

нуля предел lim

k

( 0 k ),

не является

n v

n

очевидным.

то ряды (1) и (2) одновременно сходятся

или одновременно расходятся

Признак

К рядам, общий

Пусть дан ряд

u n

и существует предел

Даламбера

член ряда которых

n 1

содержит a n или n!

un 1

lim

d , то

n u

n

если d 1, то ряд сходится;

если d 1, то ряд расходится ;

если d 1, то вопрос остается нерешенным .

Признак

К рядам, из общего

Пусть дан ряд

u n

и существует предел

Коши

члена которых

n 1

извлекается корень

n-ой степени

29