Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Ухтинский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

методичка 2 курс 3 семестр3 1911

.pdf

Скачиваний:

Добавлен:

02.03.2016

Размер:

1.04 Mб

Скачать

☆

<<< < Предыдущая 12 / 42 3 4 > Следующая >>>

f (x, y, z)dS

f (x( y, z), y, z) dydz

Dyz

f (x, y, z)dS

f (x( y, z), y, z)

)

dydz

(xy

(xz

Dyz

f (x, y, z)dS

f (x, y(x, z), z)

)

dxdz

( yx )

( yz

Dx z

6. Формула Остроградского – Гаусса в векторной форме имеет вид:

d divF

rotF n0 d

d dV

Производная

скалярной

функции

u u(x, y, z)

по направлению

вектора вычисляется по формуле:

cos

U cos

cos

8. Дивергенция векторного поля a 2x yz i

2y zx j 2z xy k равна:

3) –yz – zx – xy

2x +2y+2z

Ряд вида un

, где un

- члены числовой последовательности, называется:

n 1

числовым

степенным

рядом Фурье

рядом Лорана

10. Найти интервал сходимости степенного ряда

n 1

(-1; 1)

( ; )

точка x 0

(-2; 0]

11.Разложение функции

f (x) по степеням x (в ряд Маклорена) имеет вид:

(n)

(0)

f (x)

f (0)

(0)

f (0)

...

xn ...

( n)

(1)

2) f (x) f (1)

(1)

(x 1)

f (1)

(x 1)2

...

(x 1)n ...

3) f (x) f (0)

f (0)

x 2

f (0)

...

f (n) (0)

x n ...

4) f (x) 1

x 2

...

x n

...

12. Разложением в ряд Фурье функции f(x) = x, определенной внутри интервала (-π; π) и повторяющейся периодически вне этого интервала с периодом 2π, будет:

1) 2

1 n 1

cos nx sin nx

1 n 1

cos nx

n 1

3) 1 n 1

sin nx

1 n 1

sin nx

n 1

13. Дифференциальное уравнение y y2 x называется::

1) Уравнением с разделяющимися

2) Линейным уравнением

переменными

3) Уравнением Бернулли

4) Однородным уравнением

14. Решить уравнение y

( y )

15. Вычислить двойной интеграл dx (x 2 y) dy .

16. Вычислить криволинейный интеграл 2-го рода

(2 4 y)dx (2x 3y)dy ,

если кривая интегрирования L : y = x3; от т.О(0,0) до т.А(1,1).

17. Найти градиент скалярного поля

u sin x sin y cos z 5xyz в точке

M (0; 0; ) .

18. Вычислить поток поля

а(М ) хi

(2y xz) j 3k через поверхность S -

замкнутая

поверхность,

образованная

цилиндром

x2 y2 9 и

плоскостями

z 0, z 2 .

19. Дан ряд: 1

...

... . Исследовать на сходимость.

Найти сумму

2n 1

ряда.

20. Вычислить приближенно с точностью до 0,001: 3 9 .

3.5. Билет 5 (кратные интегралы, криволинейные интегралы, теория поля, ряды) – комбинированный: тест+задачи с выбором уровня сложности

	1	1 x
1. Областью интегрирования интеграла dx f (x, y)dy является:
	0	0
1)	прямоугольник		2) квадрат
3)	треугольник		4) окружность
2. Объем тела, занимающего область Т, определяется по формуле:
1)	V y dx dy dz	2) V xyz dx dy dz
	T		T
3)	V dx dy dz	4) V	1	dx dy dz
3)	V dx dy dz	4) V		dx dy dz
	T	3		T
	T
3. Криволинейным интегралом 1-го рода является следующий интеграл:
1)	f (x, y)dxdy	2) f x, y, z dV
	D			V
3)	f (x, y) dl	4) P(x, y)dx Q(x, y)dy
	AB			AB

4. Работа силового поля F P(x, y, z);Q(x, y, z), R(x, y, z) на криволинейном участке АВ находится по формуле:

1)	Pdx Qdy			2)	Pdx Qdy Rdz
	AB				AB
3)	P	Q	R	4)	Pdx Qdy
	x	y	z		AB
					AB

5. Формулой Остроградского-Гаусса, устанавливающей связь между поверхностным интегралом 2-го рода и тройным интегралом является:

1)		Pdydz Qdxdz Rdxdy P Q R dxdydz
		V
2)
2)	Pdydz Qdxdz Rdxdy Px			Qx		Rx dxdydz
		V
3)		Pdydz Qdxdz Rdxdy dxdydz
		V
4)
4)		Pdydz Qdxdz Rdxdy Px	Qy		Rz dxdydz
		V

6. Дан поверхностный интеграл 1-го рода. Если уравнение поверхности задано в явном виде z=z(x, y), то целесообразно пользоваться формулой:

1)		f (x, y, z)dS f (x, y, z(x, y))		2			2	dxdy
1)		f (x, y, z)dS f (x, y, z(x, y))	1 (zx )		(z y )			dxdy
	S	Dxy
2)		f (x, y, z)dxdy f (x, y, z(x, y))dxdy
	S	Dxy
3)		f (x, y, z)dS f (x( y, z), y, z)		2		)	2	dydz
3)		f (x, y, z)dS f (x( y, z), y, z)	1 (xy )		(xz	)		dydz
	S	Dxy
			13

f (x, y, z)dS

f (x, y(x, z), z)

)

dxdz

1 ( yx )

( yz

Dxy

7. Градиентом скалярного поля u x2 y3 z в точке

M ( 1; 1;2) является вектор:

1) 4i

6 j k

2) 2i

3 j 2k

3) i

4) 2i

8. Ротор rot a

векторного поля a P(x, y, z)i

Q(x, y, z) j R(x, y, z) k вычисляется

по формуле:

P i

R k

9. Обобщенно-гармонический ряд

сходится при условии:

n 1

p 0

p 1

0 p 1

p 1

10. Множество числовых значений аргумента x, при которых степенной ряд

an xn сходится, называется:

n 1

суммой ряда

радиусом сходимости

общим членом ряда

интервалом сходимости

11.Разложение функции ex2 по степеням x (в ряд Маклорена) имеет вид:

1) ex2

...

2) e x2

...

x2n

...

(2n)!

3) ex2

...

x2n

...

4) e x2

...

x4n

...

(2n)!

12. Коэффициенты вида

f x dx ,

f x cosnxdx ,

f x sin nxdx ряда

an cosnx bn sin nx называются

n 1

коэффициентами:

Лорана

Коши

Фурье

Тейлора

Задания 13-16 предполагают различный уровень сложности: задания под буквой А). – удовлетворительно; задания под буквой Б). – хорошо; Задания под буквой Б). + задание 17 - отлично

13.

А). Вычислить двойной

Б).

Найти

объем

тела,

заданного

ограничивающими

его

поверхностями:

интеграл dy

(x 2 y)dx .

z 4 .

-3

y 2 4

14.

А). Вычислить криволинейный интеграл 2-

го рода	xdx 2 y 2 dy ,		если
	L
кривая	интегрирования L :
y = 2x2;	от	А(1,2)	до
В(2,8).

Б). Вычислить криволинейный интеграл 2-го

рода (z 3x) dx 2 y 2 dy 2x dz ,	заданный по
L
пространственной кривой L – замкнутому
контуру треугольника ABС	с вершинами
A(2;0;0) , B(0;3;0) , С(0;0;1) ,	если контур

треугольника задать, как пересечение плоскости

3x 2y 6z 6 0	с	координатными
плоскостями x 0, y 0, z 0 .

15.

А).			Найти					div					F , если			Б). Проверить, является ли векторное поле
					xy					y						гармоническим:
	F 2xi						j					k .				гармоническим:

																			y
					z					z	2						1		y					1		z								1	x
											2					F		z		x	2	i					y		2	j								2 k
																F					2	i							2	j								2 k
																									x									y			z
16.
А). Дать название ряду:																		Б). Найти область сходимости ряда.
1			1			1								1 n 1				Выяснить сходимость на концах
1									...						....			интервала сходимости:
1		32		52		72			...					(2n 1)2	....			интервала сходимости:
Исследовать на сходимость.																		1		2x			3		(2x			3)3				(2x				3)5		...
Исследовать на сходимость.																		1

																			5			2				52	3							53	4
																										0, 4sin x x
17. Вычислить приближенно с точностью до 0,001:																																	dx .
17. Вычислить приближенно с точностью до 0,001:																													x		2		dx .
																										0			x

4. СПРАВОЧНЫЕ МАТЕРИАЛЫ

4.1. Дифференциальные уравнения.

№

Вид уравнения

Способ решения

Дифференциальные уравнения I порядка. Дифференциальным уравнением первого порядка называется соотношение,

связывающее функцию, ее первую производную и независимую переменную, т.е. соотношение вида: F(x, y, y ) 0

Если такое соотношение преобразовать к виду y f (x, y) то это дифференциальное уравнение первого порядка будет называться уравнением,

разрешенным относительно производной.

Общим решением дифференциального уравнения называется такая дифференцируемая функция y = (x, C), которая при подстановке в исходное уравнение вместо неизвестной функции обращает уравнение в тождество.

Решение вида у = (х, С0) называется частным решением дифференциального уравнения.

Задачей Коши называется нахождение любого частного решения дифференциального уравнения вида у = (х, С0), удовлетворяющего начальным условиям у(х0) = у0.

Уравнения

разделяющимися

Перенести одно из слагаемых в правую

переменными.

часть.

M ( y) P(x) dx N(x) Q( y) dy 0

Собрать с одной стороны равенства

( M ( y) P(x) N(x) Q( y) y 0 )

переменную х, с другой стороны

равенства у.

P(x)

Q( y) dy

N (x)

M ( y)

Проинтегрировать

правую

и левую

части равенства.

Записать общее решение:

Q( y)

dy c

P(x)

M ( y)

N (x)

Найти особое решение из уравнения:

M ( y) N(x) 0

Однородное уравнение

Проверить

однородность

функций

P(x, y) dx Q(x, y) dy 0

P(x, y); Q(x, y)

( P(x, y) Q(x, y) y 0)

P( x, y) n P(x, y)

Q( x, y) nQ(x, y)

Сделать

замену

y tx ,

dy tdx xdt

( y xt t) .

Получаем

уравнение

разделяющимися переменными.

Линейное уравнение

Делаем замену

p(x) y g(x)

y uv, y

u v uv

Получаем систему уравнений:

v p(x) v 0 v(x)

u(x, c)

u v g(x)

Находим общее решение:

y v(x) u(x, c)

Уравнение Бернулли

Делаем замену

y p(x) y g(x) y

, n 0, n 1

y uv, y

u v uv

Получаем систему уравнений:

p(x) v 0 v(x)

u unvn 1g(x) u(x, c)

Находим общее решение:

y v(x) u(x, c)

Уравнение

полных

проверяем

выполнение

условия

дифференциалах

P x; y dx Q x; y dy 0

, ищем

если его левая часть полный

P x; y и

u Q x; y

дифференциал

некоторой

функции

u x; y ,

т.е. P x; y dx Q x; y dy du(x; y) .

Решение

записываем

виде

u x; y С .

Дифференциальные уравнения II порядка

В общем случае дифференциальное уравнение второго порядка можно записать в виде

где F − заданная функция указанных аргументов.

Если дифференциальное уравнение можно разрешить относительно второй производной y'', то его можно представить в следующем явном виде:

Общим решением дифференциального уравнения называется такая дифференцируемая функция y = (x, C1, С2), которая при подстановке в исходное уравнение вместо неизвестной функции обращает уравнение в тождество.

Решение вида у = (х, С10, С20) называется частным решением дифференциального уравнения.

Задачей Коши называется нахождение любого частного решения дифференциального уравнения вида у = (х, С10, С20), удовлетворяющего начальным

условиям у(х		) у	,	у (х	) у .
0		0		0	0
Дифференциальные уравнения второго порядка, допускающие понижение
						порядка.
6	Уравнения вида y				f (x)		Порядок	понижается	путем
							двукратного	интегрирования
							уравнения.
							y f (x)dx 1 (x) c1
							y ( 1 (x) c1 )dx 2 (x) xc1 c2
						17

Уравнение не содержит явно у

Делаем

замену

y p(x) ,

тогда

y p

F(x, y , y )

f (x, p)

Уравнение принимает вид p

– уравнение первого порядка.

Пусть p (x, c1 ) общее решение.

Делая обратную замену, получаем

y (x, c1 ) и y (x, c1 )dx c2

Уравнение не содержит явно х

Делаем

замену

y p( y) ,

тогда

F( y, y , y )

p dy

Уравнение

принимает

вид

f ( y, p) – уравнение

первого

порядка.

Пусть p ( y, c1 ) общее решение.

Делая обратную замену, получаем

y ( y, c1 )

x c2

( y, c )

Линейные однородные дифференциальные уравнения с постоянными

коэффициентами (ЛОДУ).

y py qy 0

Составляем

характеристическое

уравнение

k 2 pk q 0

Если k1 k2

Общее решение y C ek1x

ek2x

Если k1 k2

Общее решение y C ekx

xekx

Если k1,2

Общее решение

y e x (C cos x C

sin x)

Линейные неоднородные дифференциальные уравнения с постоянными

коэффициентами (ЛНДУ).

y py qy f (x)

Общее решение y y y *,

где y -

общее решение ЛОДУ, y * -

частное решение ЛНДУ

y * можно

найти методом вариации

Составляем систему

произвольной постоянной

C y C y

y* C1 (x) y1 C2 (x) y2

f (x)

C1 y1 C2 y2

Решив систему, найдем C1 и

C2 . Затем

найдем

C1 (x) C1dx

Найденные

значения

C2 (x) C2 dx .

подставляем в y *

y * можно найти по виду правой части

f (x)

f (x) Pn x

Если

не

является

корнем

характеристического

уравнения, то

y* Qn

Если 0 является корнем кратности r

характеристического уравнения, то

y* xr

f (x) Pn x e x

Если

не

является

корнем

характеристического уравнения, то

y* e x Q

Если α является корнем кратности r

характеристического уравнения, то

y* xr e x Q x

f (x) Pn x cos x Qm x sin x

Если

βi

не

является

корнем

характеристического уравнения, то

y* M s x cos x Ns

x sin x

s max{n, m}

Если βi является корнем кратности r

характеристического уравнения, то

y* xr [M

x cos x N

x sin x]

s max{n, m}

f (x) e x [P x cos x Q x sin x]

Если

α+βi

не

является

корнем

характеристического уравнения, то

y* e x [M

x cos x N

x sin x]

s max{n, m}

Если α+βi является корнем кратности r

характеристического уравнения, то

y* xr e x [M

x cos x N

x sin x]

s max{n, m}

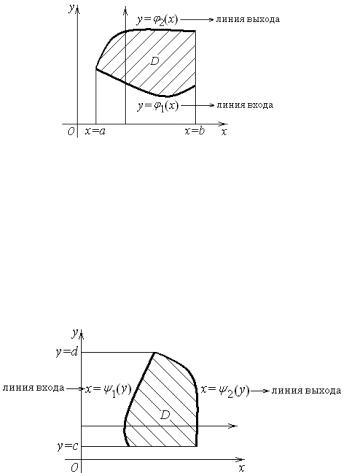
4.2. Кратные интегралы

Двойной интеграл

f x;y dxdy			n	xi ; yi Si
f x;y dxdy		lim	f	xi ; yi Si
		n
D		max di 0 i 1
Вычисление двойного интеграла в декартовых координатах
1. Область, правильная в направлении оси Oy
Область интегрирования D ограничена слева и справа прямыми					x a	и x b
( a b ), а снизу и сверху	– непрерывными			кривыми y 1 x	и	y 2 x

( 1 x 2 x ), каждая из которых пересекается вертикальной прямой только в одной точке.

Для такой области двойной интеграл вычисляется по формуле

	b	2 x
	f x;y dxdy dx	f	x;y dy ,
D	a	1 x
2. Область, правильная в направлении оси Ox
Область интегрирования D	ограничена снизу и сверху прямыми			y c	и y d
( c d ), а слева и справа	– непрерывными		кривыми x 1 y	и	x 2 y

( 1 y 2 y ), каждая из которых пересекается горизонтальной прямой только в одной точке.

Для такой области двойной интеграл вычисляется по формуле

			d	2 y
		f x;y dxdy dy f			x;y dx
		D	c	1 y
	Вычисление двойного интеграла в полярных координатах
если область D*		ограничена лучами и			,	где , и кривыми
r r	и r r	, где r	r ,	т. е.	область	D* правильная: луч,
1	2	1	2

выходящий из полюса, пересекает ее границу не более чем в двух точках, то интеграл можно записать в виде

<<< < Предыдущая 12 / 42 3 4 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
14.07.2019853.31 Кб8Методика сокращенного многофакторного обследова....docx
#
02.03.2016453.12 Кб5МЕТОДИЧЕСКИЕ УКАЗАНИЯ к курсовой работе НГД.doc
#
02.03.2016494.25 Кб8Методические указания кконтрольной работе_ЭНП.pdf
#
06.12.2018501.25 Кб3МЕТОДИЧЕСКИЕ УКАЗАНИЯ РЭНГ, ПЭМГ, БС .doc
#
24.08.20191.36 Mб2Методическое пособие 2006г..doc
#
02.03.20161.04 Mб24методичка 2 курс 3 семестр3 1911.pdf
#
07.05.2019240.61 Кб2Методичка 15.02.docx
#
02.03.2016381.18 Кб12Методичка Англ. яз. II вариант.pdf
#
02.03.2016147.46 Кб13методичка для офрмления диплома.DOC
#
02.03.20162.53 Mб33Методичка к курсачу.doc
#
02.03.2016381.95 Кб7Методичка МВКО.doc