
- •Высшая математика
- •Глава I Общие методические указания
- •§1. Порядок выполнения контрольных работ
- •§2. Программа курса "Высшая математика"
- •Библиографический список
- •Глава II Указания к выполнению контрольных работ
- •§1. Аналитическая геометрия на плоскости
- •5.1. Уравнение прямой с угловым коэффициентом имеет вид
- •§2. Аналитическая геометрия в пространстве
- •§3. Элементы высшей алгебры
- •§4. Введение в анализ
- •5. Дифференцирование
- •Вопросы для самопроверки к контрольной работе №1
- •Контрольная работа №1 Векторы. Элементы высшей алгебры
- •Вопросы для самопроверки к контрольной №2
- •Контрольная работа №2 Аналитическая геометрия
- •Вопросы для самопроверки к контрольной №3
- •Контрольная работа №3 Введение в математический анализ, производная, приложения производной
- •Оглавление
§3. Элементы высшей алгебры
1. Определители.
Определителем второго порядка называется число, определяемое равенством:
a
 11
a12
11
a12
= a11 a22 - a12 a21.
a21 a22
Определителем третьего порядка называется число, обозначаемое
символом:
=
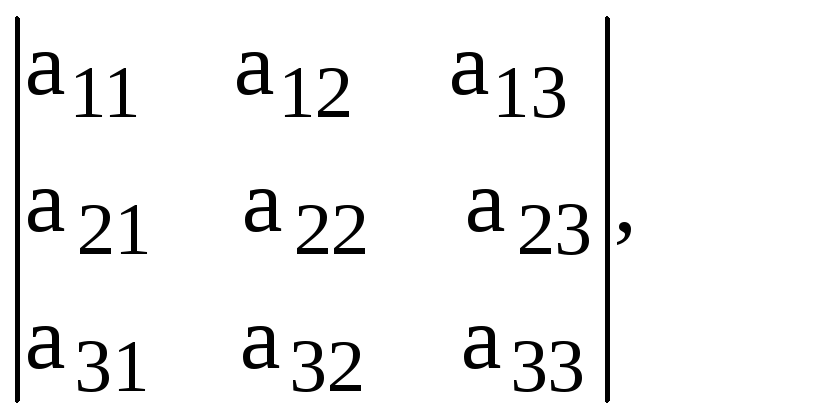
определяемое равенством:





 a22
a23
a21 a23
a21 a22
a22
a23
a21 a23
a21 a22
= a11 - a12 + a13 .
a32 a33 a31 a33 a31 a32
2. Матрицы.
Матрицей размерностью т на п называется таблица чисел, содержащая т строк и п столбцов. Обозначается матрица А(т x п).

 a11 a12 ... a1n
a11 a12 ... a1n
a21 a22 ... a2n
А = - - ... -
am1 am2 ... amn .
Числа аij называются элементами матрицы А; i – номер строки, j – номер столбца.
Матрица, получаемая из матрицы А переменой местами строк и столбцов, называется транспонированной матрицей и обозначается AT.
Матрица, у которой m = п, называется квадратной.
1
 0 ... 0
0 ... 0
0 1 ... 0
Квадратная матрица вида: - - - -
0 0 ... 1
называется единичной матрицей и обозначается Е.
3. Действия с матрицами.
3.1. Сложение матриц.
Можно складывать матрицы одинаковой размерности:
А(т x п) + В(т x п) = С(m x n).
Элементы матрицы-суммы С определяются формулами: сij = аij+ bij.
3.2. Умножение матрицы на число
· А(m x n) = В{m x n).
Элементы матрицы В определяются формулами: bij = · aij .
3.3. Умножение матрицы на матрицу
А(т х п) » В(п хр) = С(т х р).
Если количество столбцов первой матрицы А равно числу строк второй матрицы В, то произведение А В существует. В противном случае говорят, что А В не существует.
Элементы
матрицы С
определяются
формулами:![]() =
=![]() .
.
4. Обратная матрица.
Матрицей, обратной матрице А(n x п), называется матрица, обозначаемая А-1 , для которой выполняется равенство:
А · А-1 =А-1 · А=Е.
Обратную матрицу ищут по формуле:

 A11 A21 ... An1
A11 A21 ... An1
A12 A22 ... An2
A-1
=
![]()
- - - - ,
- - - - ,
A1n A2n ... Ann
где – определитель матрицы А, Аij – алгебраическое дополнение элемента аij – матрицы А. Аij вычисляется по формуле Аij= (-l)i+j Мij, где Мij – минор элемента аij Мij получается из вычёркиванием i-ой строки и j -го столбца.
Пример
1. Дана матрица
А
=
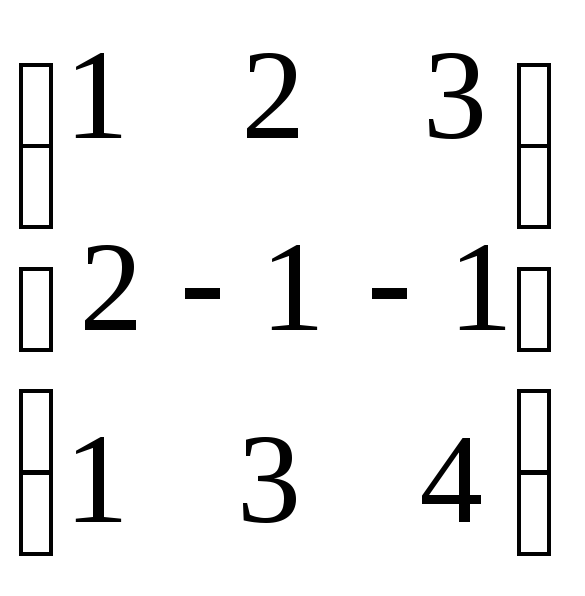 .
НайтиА-1
.
.
НайтиА-1
.

 1
2 3
1
2 3
Решение:1) ищем = 2 -1 -1 =2, 0, поэтому А-1 существует.
1 3 4
2) ищем Аij:



 -1 -1 2 -1
-1 -1 2 -1
A11 = (-1)1+1 = -4+3=-1; A12 = (-1)3 = -(8+1)=-9;
3 4 1 4



 2 -1 2 3
2 -1 2 3
A13 = (-1)4 = 6+1 = 7; A21 = (-1)3 = -(8-9)=1;
1 3 3 4



 1 3 1 2
1 3 1 2
A22 = (-1)4 = 4-3 = 1; A23 = (-1)5 = -(3-2)=-1;
1 4 1 3



 2 3 1 3
2 3 1 3
A31 = (-1)4 = -2+3 = 1; A32 = (-1)5 = -(-1-6)=7;
-1 -1 2 -1

 1 2
1 2
A33 = (-1)6 = -1-4 = -5.
2 -1
А-1
=
![]()
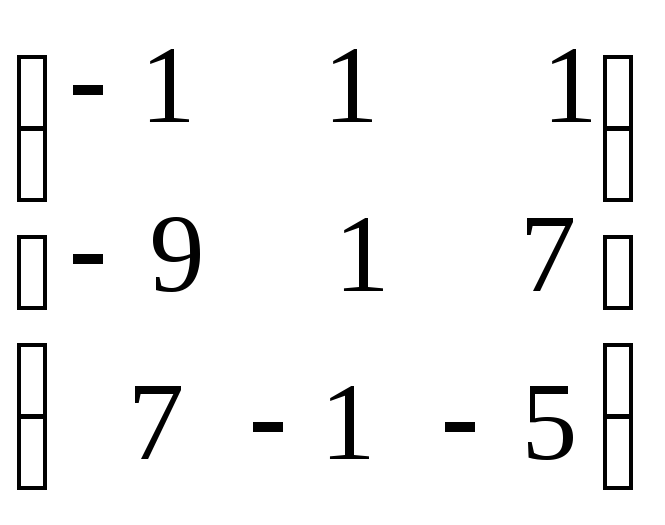 .
.
Проверяем
правильность вычислений
![]() .
.
5.1. Системы трёх уравнений первой степени с тремя неизвестными.
Рассмотрим систему трёх уравнений первой степени с тремя неизвестными x, у, z:
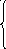
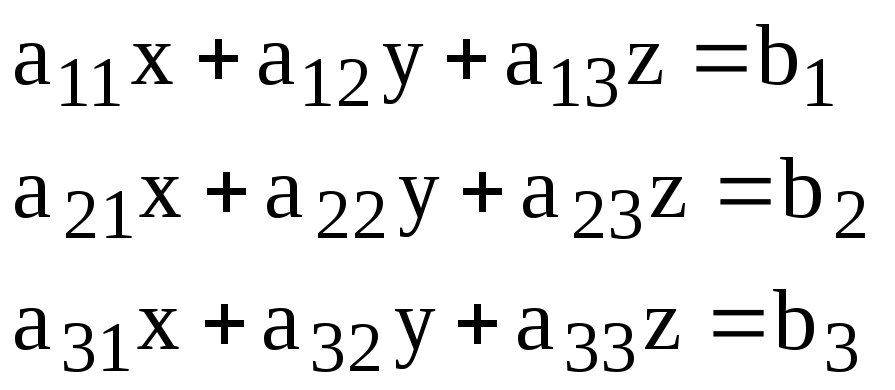 ,
,
где аij – заданные коэффициенты, bi – свободные члены.
5.2. Метод Крамера.
Считаем определители:
=
 x
=
x
=
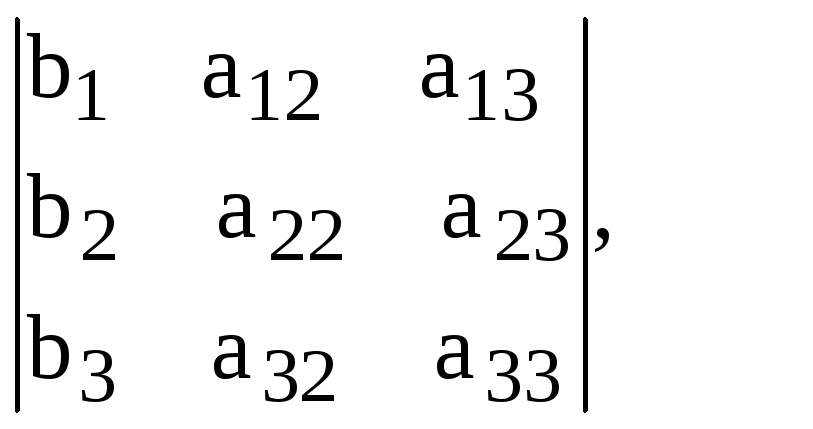
y
=
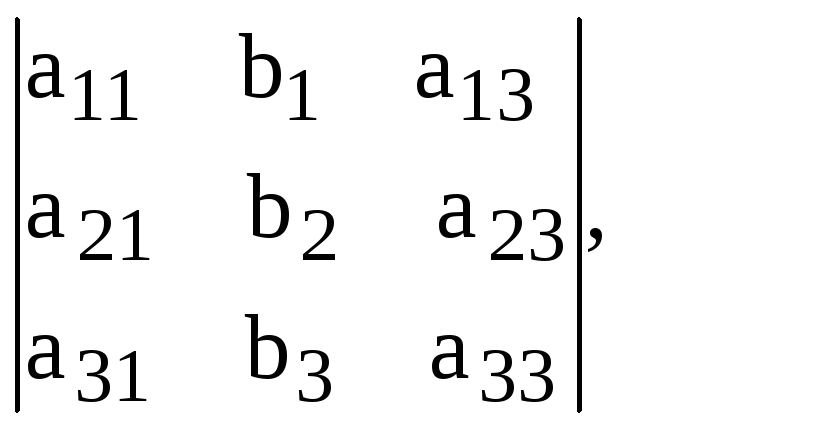 z
=
z
=
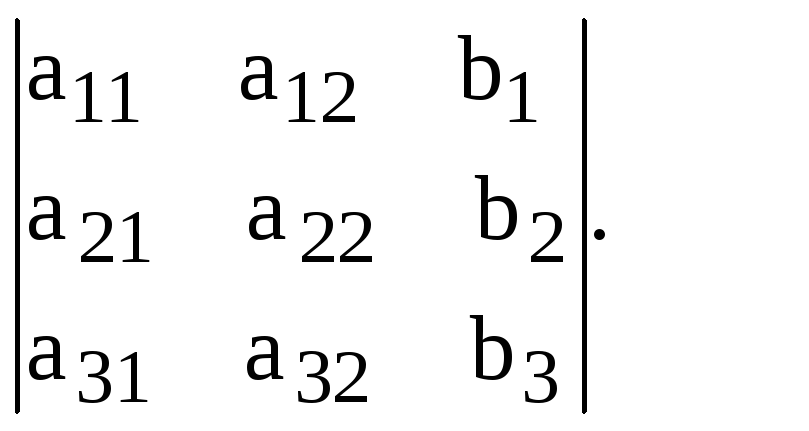
Если определитель системы 0, то существует единственное решение этой системы, и оно выражается формулами:
![]()
![]() .
.
5.3. Матричный метод.
Выписываем
матрицу А
системы: А
=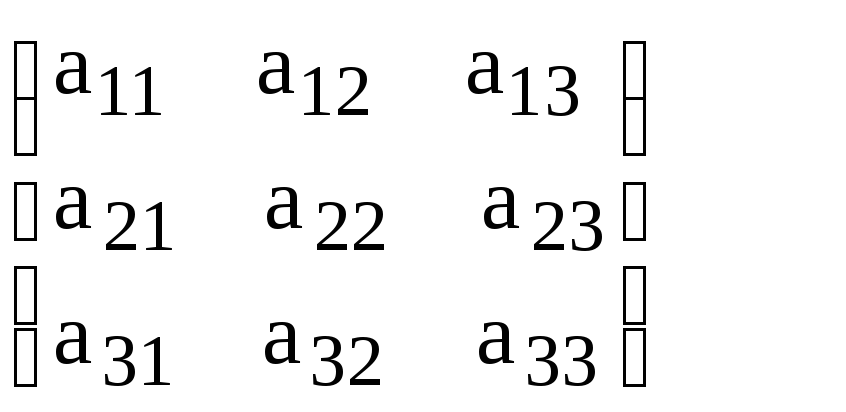
и находим A-1. Если А-1 существует, то решение ищем по формуле:
![]() =
A-1B,
=
A-1B,
где
B
– матрица-столбец свободных членов: В
=
![]() .
.
Пример
2. Решить
систему уравнений:
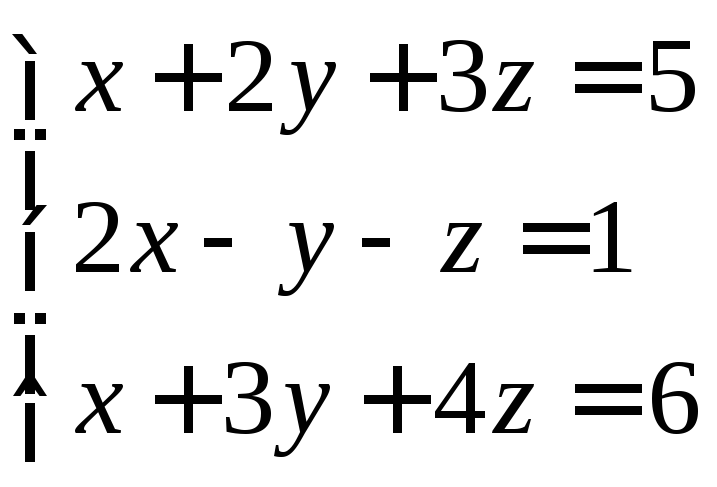 .
.
Решение:
Метод Крамера: считаем = 2; x = 2; y= -2; z= 4, тогда x = 1;y = -1; z = 2.
Матричный метод: выписываем
А
=
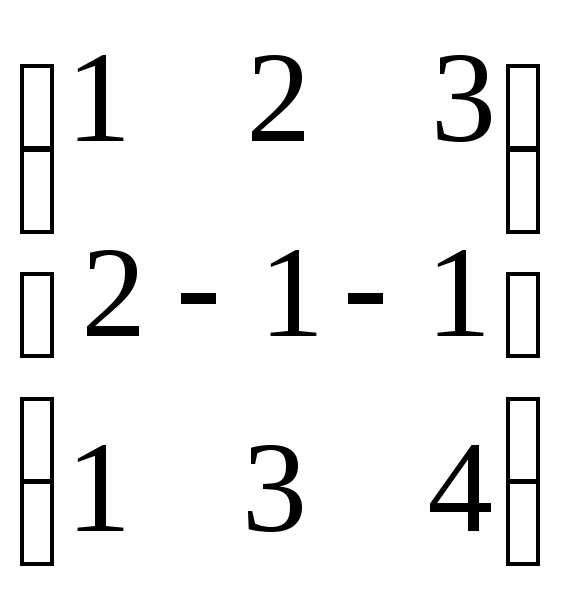 , считаемА-1
=
, считаемА-1
=
 ,
,
![]() =A-1B
=
=A-1B
=

![]() =
=![]() .
.
