§2. Аналитическая геометрия в пространстве

1. Прямоугольная система координат OXYZ в пространстве определяется заданием масштабной единицы измерения длин и трёх пересе­кающихся в одной точке О взаимно перпендикулярных осей: ОХ. ОУ и OZ.

2.Понятие вектора.

Направленный отрезок АВ называется вектором. А – начало, В – конец вектора. Вектор также обозначают и одной буквой, например . Длина вектора обозначается ||. Векторыиназываютсяколлинеарными, если они лежат на одной прямой или на параллельных прямых. Модуль вектора = (a₁; a₂; a₃) равен |.| = .

3. Линейные операции над векторами.

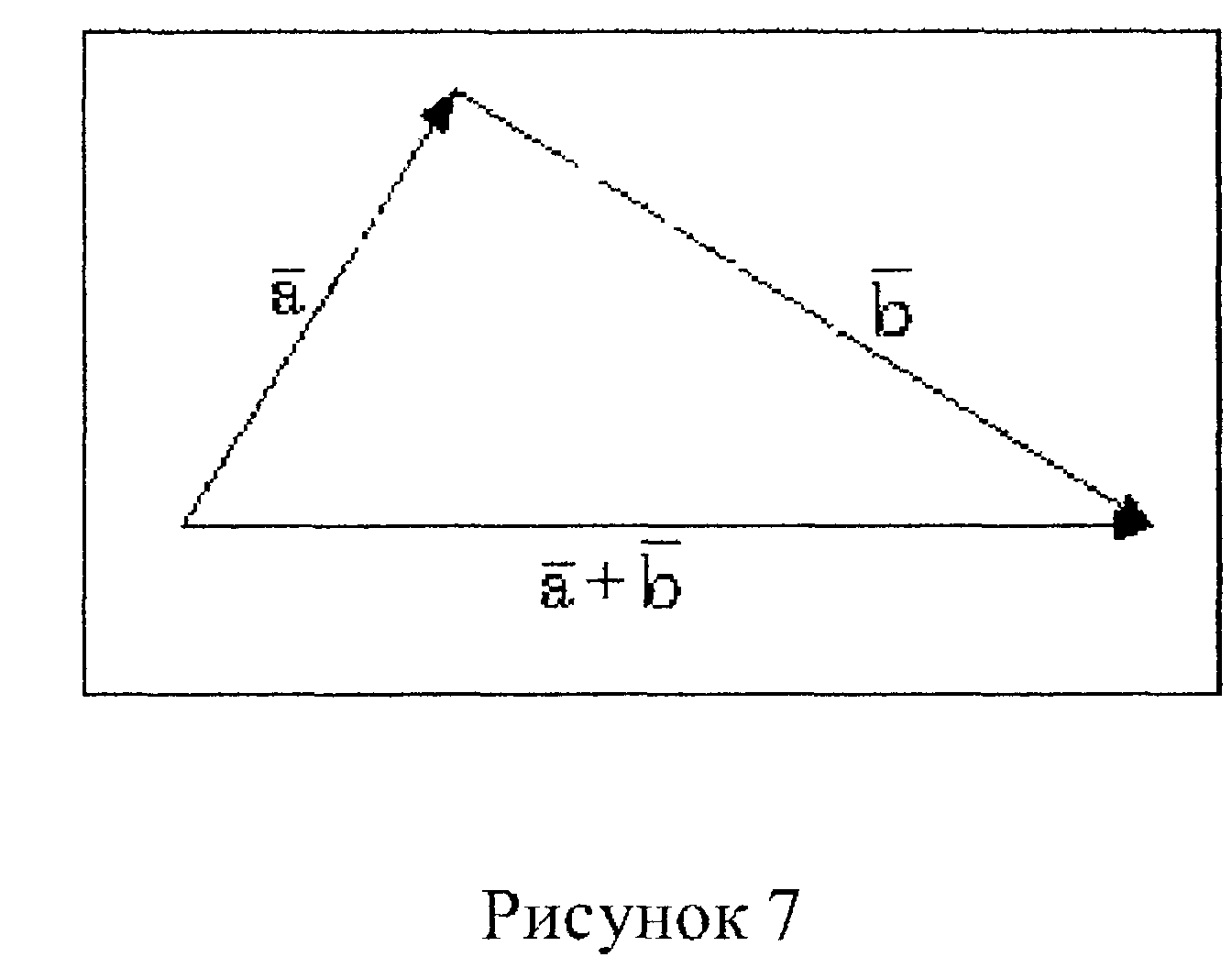
Суммой +двух векторови называется вектор, который идёт из начала вектора в конец вектора, при условии, что конец вектораи начало векторасовпадают (рис. 7).

Р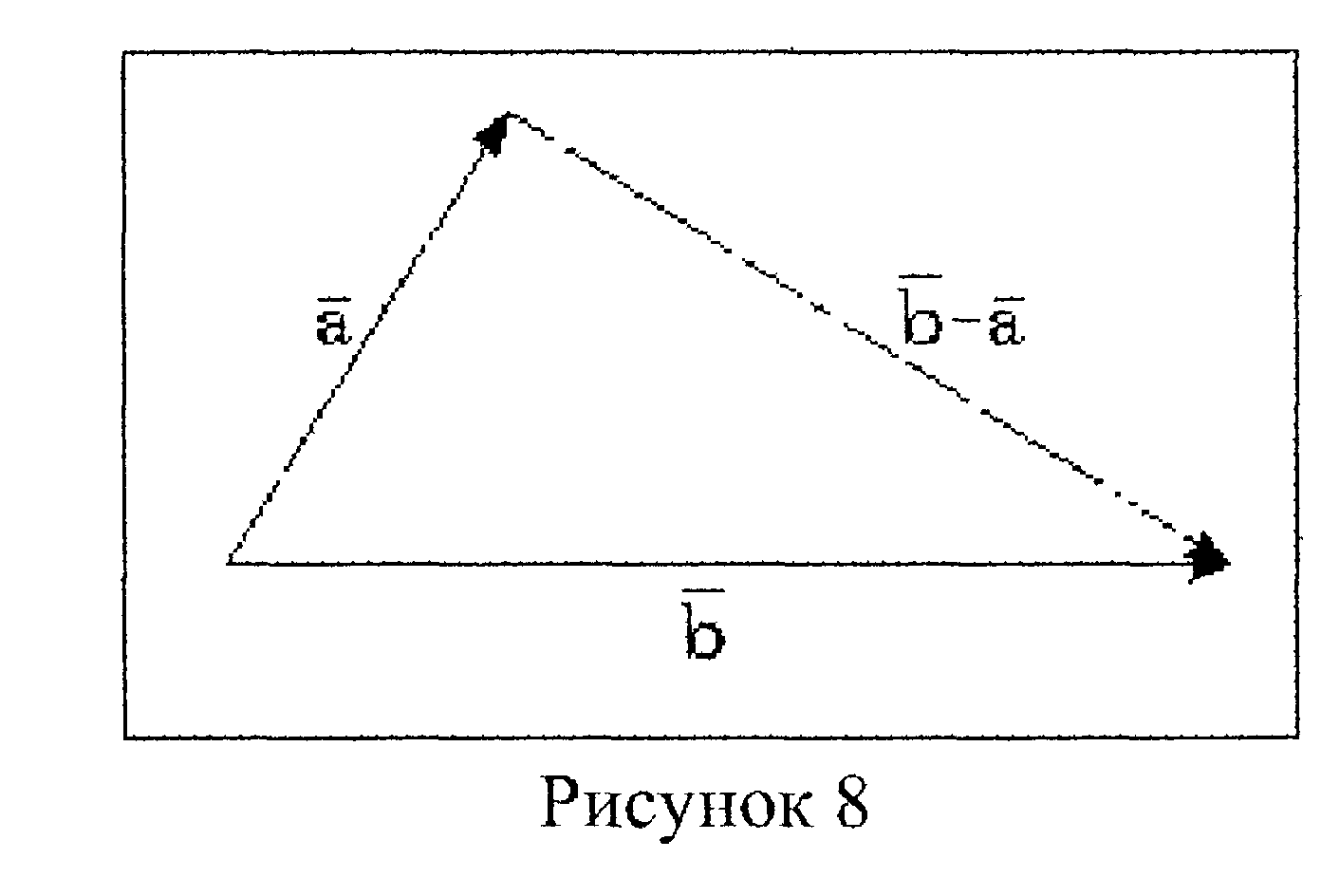азностью –двух векторовиназывается вектор, который в сумме с векторомдаёт вектор(рис. 8).

П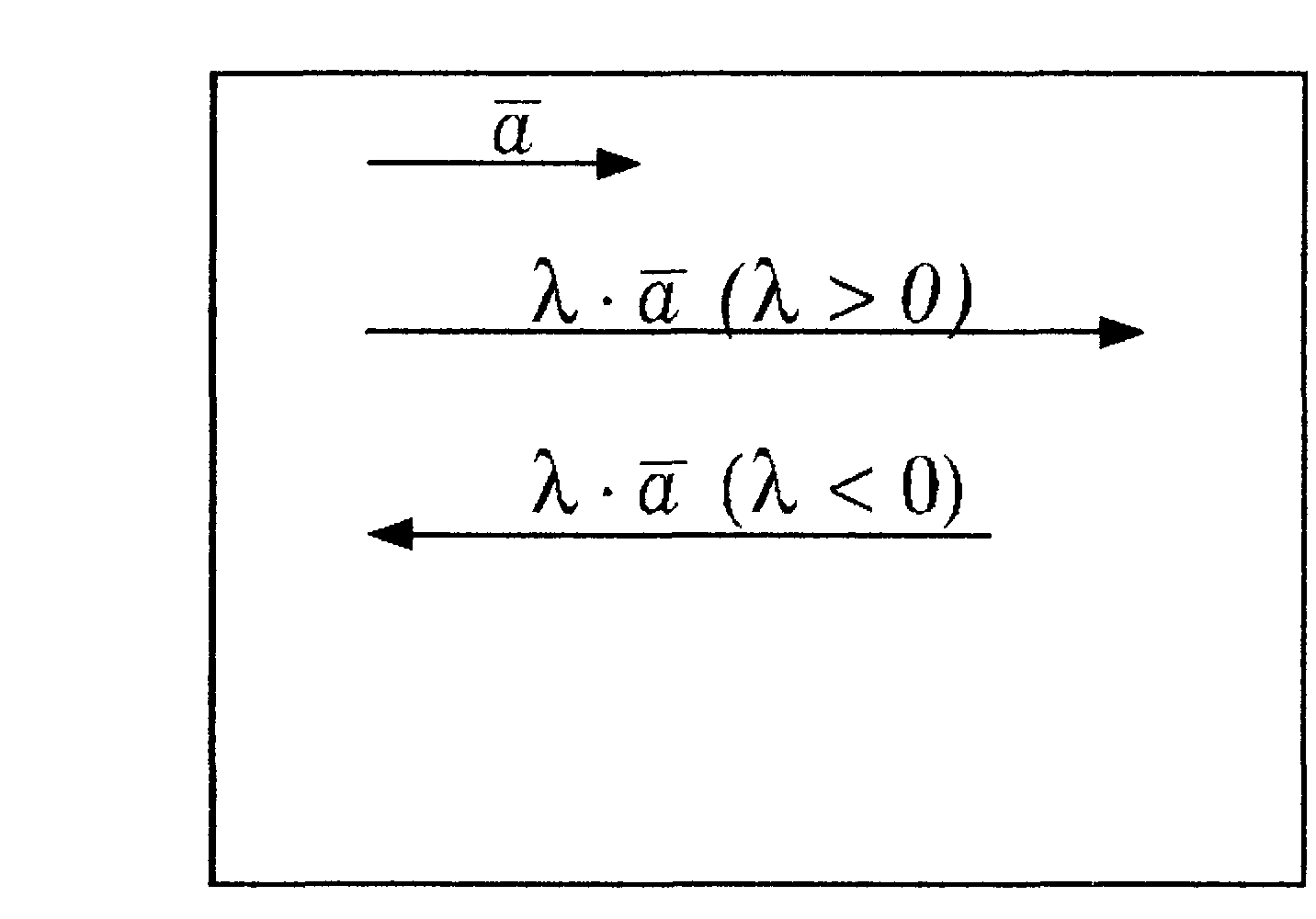роизведением  ( 0,   0) называется вектор, который коллинеарен вектору ā, направлен так же, как , если>0 и в проти­воположную сторону, если <0 и .

Рисунок 9

4. Скалярное произведение векторов.

Скалярным произведением двух векторов иназывается число , равное произведению модулей этих векторов на косинус угла между ними. Скалярное произведение обозначают.

= || || cos , где  – угол между векторами и.

Проекцией вектора на векторявляется число

Пp_b ā = | ā | cos  =. .

Если векторы изаданы своими координатами= (a₁; a₂; a₃) и

= (b₁; b₂; b₃), то их скалярное произведение определяется формулой:

= .

Пример 1. Найти угол между векторами = (1; 1; 0) и=(1;0;1), а также проекцию векторана вектор.

Решение:

cos  = = ,

следовательно, =60°. Пр_b ==.

Пример 2. Вычислить (3–2) (+2), если ||=3, || =4, угол междуиравен =2/З.

Решение: (3–2) (+2)=3 – 2 + 3  2-2  2=

=3||²  cos0° +4  ||||cos(2/3) - 4|b|²  cos0⁰ = 39 + 434 (-1/2) –

– 444 =27 – 24 – 64 = - 61.

5. Векторное произведение.

Векторным произведением вектора на векторназывается вектор, который определяется тремя условиями:

а) длина вектораравна||  ||  sin , где  – угол между векторами и;

б) векторперпендикулярен каждому из векторовиb;

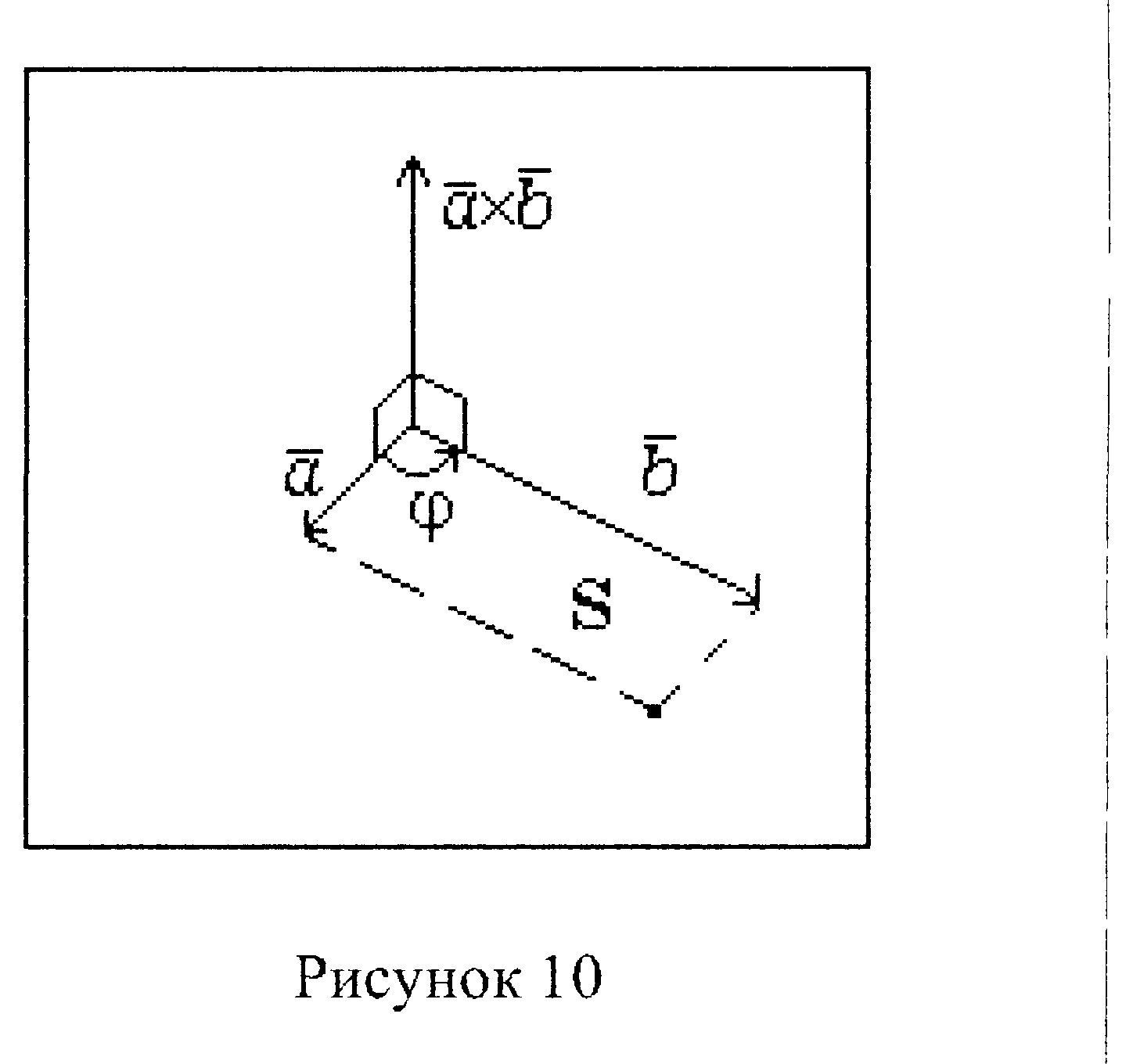
в) векторы, , образуют правую тройку векторов (рис. 10).

Если векторы изаданы своими координатами= (a₁; a₂;a₃), = (b₁;b₂;b₃), то векторное произведение вектора на векторопределяется формулой:

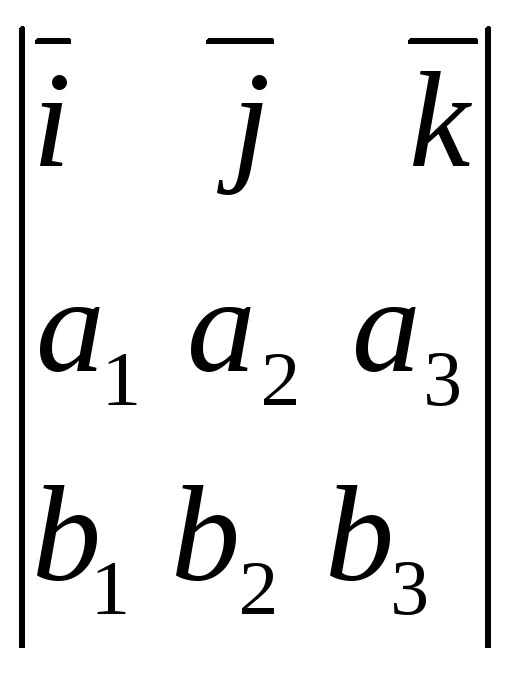= =(a₂b₃ – a₃b₂)i –(a₁b₃ – b₁a₃)j + (a₁b₂ – b₁a₂)k.

Площадь параллелограмма, построенного на векторах и, вычисляется по формулеS =  = || || sin .

Пример 3. Вычислить площадь S параллелограмма, построенного на векторах +3и 3 +, если || = || = 1 и угол между векторамииравен 30°.

Решение: (+ 3) (3 +)= 3 + 33++ 3=

= 9 ā – = 8 .

S = ( + 3) (3 + )| = |8 | = 8| = 8   |  sin30° =4

Пример 4. Даны векторы =(2; 5; 7) и= (l; 2; 4). Найти .

i j k

Решение: = 2 5 7 =(5 4 – 27)i –(2 4 - 1 7)j + (2 2 – 15)k.

1 2 4

6. Смешанное произведение векторов.

Смешанным произведением трёх векторов ,иназывается число, равное скалярному произведению векторана векторное произведение векторови, то есть . Смешанное произведение обозначают , оно определяется формулой:

=.

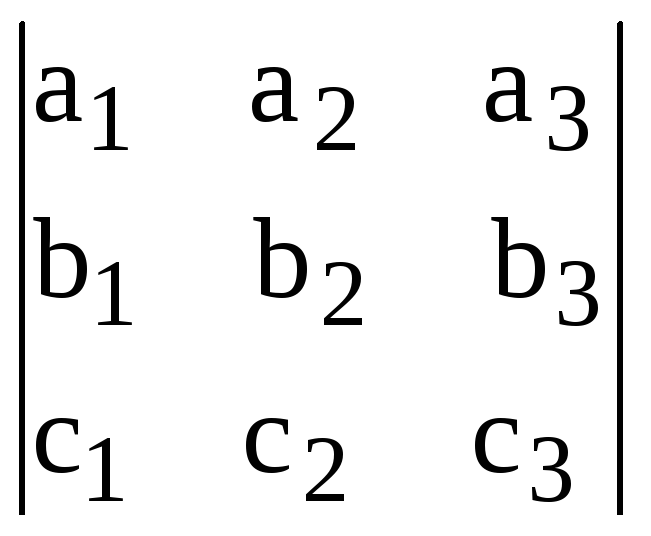Абсолютная величина смешанного произведения векторов ,иравнаобъёму параллелепипеда, построенного на векторах , и.

Пример 5. Найти объём треугольной пирамиды с вершинами

А(2; 2; 2), В(4; 3; 3), С(4; 5; 4) и D(5; 5; 6).

Решение: Объём пирамиды равен 1/6 объёма параллелепипеда, построенного на векторах АВ, АС и AD.

2 1 1

АВ=(2; 1; 1); AC =(2; 3; 2); АD=(3; 3; 4); AB AC AD= 2 3 2 =7.

3 3 4

Отсюда V_пир=7/6. Векторы,иназываютсякомпланарными, если они лежат в одной плоскости или в параллельных плоскостях Условие компланарности векторов , и:= 0.

7. Уравнение плоскости.

7.1. Общее уравнение плоскости

Ax+By+Cz+D = О.

ВекторN =(А, В, С), перпендикулярный плоскости, называется нормальным вектором этой плоскости. Угол  между плоскостями А₁x + B₁y + С₁z + D₁ = 0 и А₂x + B₂y+ C₂z + D₂ = 0 определяется по формуле cos  = , второй угол равен (180°-) .

Условие параллельности плоскостей:

N₁ || N₂ или .

Условие перпендикулярности плоскостей:

N₁  N₂, или A₁  A₂ + B₁  B₂ + C₁  C₂ = 0.

7.2. Уравнение плоскости, проходящей через три данные точки

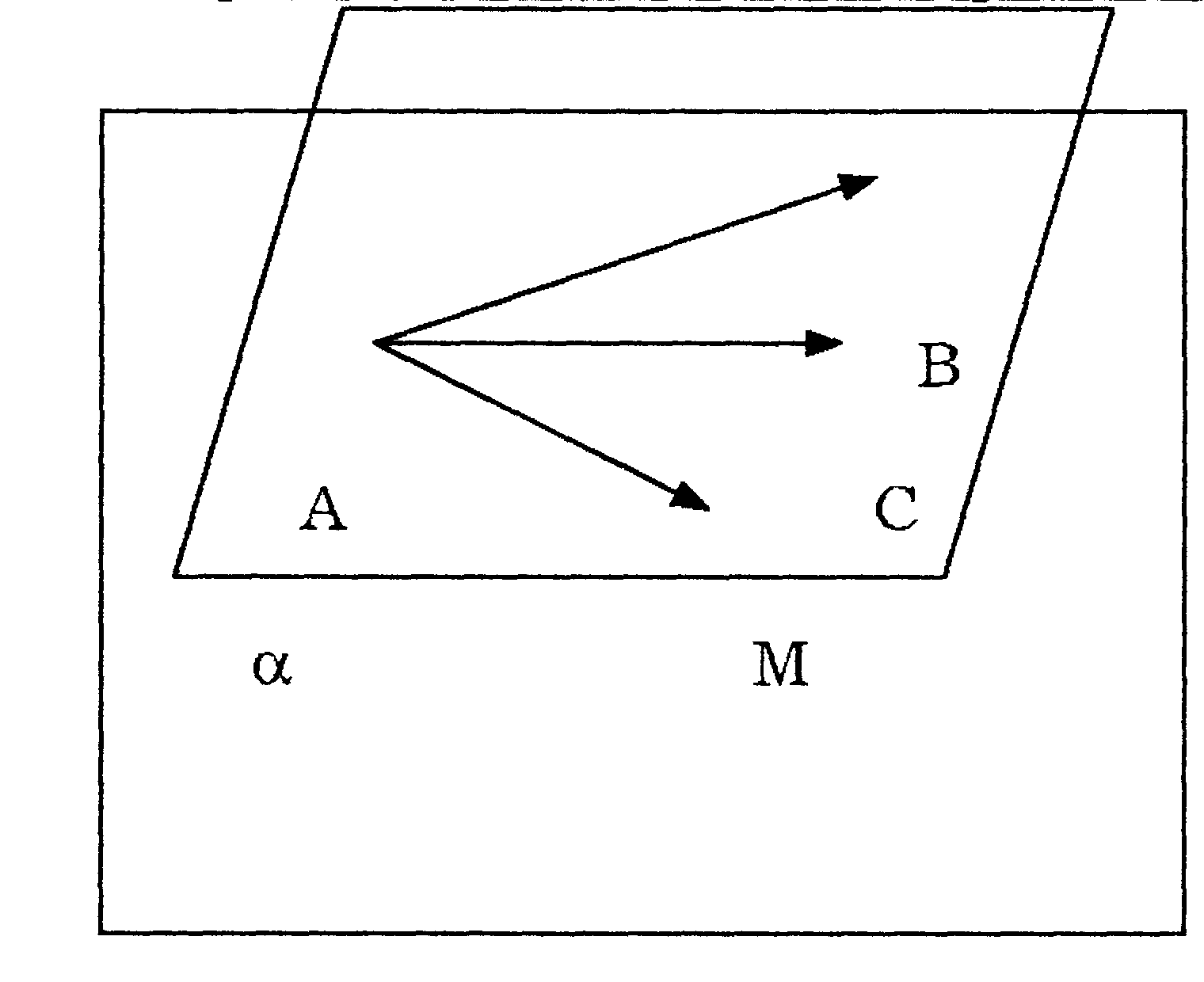
A(x₁;y₁;z₁); B(x₂;y₂;z₃) и C(x₃;y₃;z₃).

Возьмем произвольную точку М(x;у;z) а (рис. 11). Векторы компланарны= 0, следовательно,

Рисунок 11 x-x₁ y-y₁ z-z₁

x₂-x₁ y₂-y₁ z₂-z₁ = 0.

x₃-x₁ y₃-y₁ z₃-z₁

8. Уравнение прямой.

8.1. Прямая определяется совместным заданием уравнений двух плоскостей

А₁x + B₁у + С₁z + D₁ =0

А₂x + В₂у + C₂z + D₂ =0.

8.2. Канонические уравнения прямой:

,

где вектор ā = (l, m, п) – направляющий вектор прямой, проходящей через точку M₀(x₀;y₀;z₀).

8.3. Уравнение прямой, проходящей через две данные точки

M₁(x₁;y₁;z₁) и M₂(x₂;y₂;z₂) имеет вид:

.

9. Угол между прямыми.

Угол между двумя прямыми, заданными их каноническими уравнениями:

и

определяется по формуле: cos  = .

10. Угол между прямой и плоскостью Ах+By+Cz+D = 0 определяется по формуле:

sin  = .

Условие параллельности прямой и плоскости:

Al + Bm + Cn = 0;

условие перпендикулярности прямой и плоскости:

.

Пример 5. Составить уравнение плоскости, проходящей через точку M₀(1;1;1) перпендикулярно вектору N =(2; 2; 3).

Решение. Так как вектор N является нормалью для искомой плоскости, то :

2х + 2у + 3z + D = 0.

Подставляя координаты точки M₀ , имеем: 2 +2 +3 + D=0 => D = -7.

Искомое уравнение имеет вид 2х +2 y+3z -7=0.