Электростатика постоянный электрический ток электромагнетизм Основные законы и формулы

• Закон Кулона

,

где F – сила взаимодействия точечных зарядов q₁ и q₂;

r – расстояние между зарядами;

 – диэлектрическая проницаемость среды;

₀ – электрическая постоянная (₀=8,8510^-12 Ф/м).

• Напряженность и потенциал электрического поля:

,

где F – cила, действующая на единичный точечный положительный заряд q₀, помещенный в данную точку поля;

Π – потенциальная энергия точечного положительного заряда q₀, находящегося в данной токе поля.

• Напряженность и потенциал поля, создаваемого системой точечных зарядов (принцип суперпозиции, или наложения, электрических полей):

, ,

где ,– напряженность и потенциал в данной точке поля, создаваемого

i-ым зарядом.

• Напряженность и потенциал поля, создаваемого:

1. точечным зарядом

, ,

где r – расстояние от заряда q до точки, в которой определяются напряженность и потенциал;

2) проводящей заряженной сферой радиусом R на расстоянии r от центра сферы:

а) Е = 0; (приr<R);

б) ;(приr=R);

в) ;(приr>R).

• Линейная плотность заряда

,

где l – длина заряженного тела.

• Поверхностная плотность заряда

.

• Напряженность поля, создаваемого бесконечно длинной равномерно заряженной линией или бесконечно длинным цилиндром на расстоянии r от нити или оси цилиндра:

,

где  – линейная плотность заряда.

• Напряженность поля, создаваемого бесконечной равномерно заряженной плоскостью:

,

где  – поверхностная плотность заряда.

Напряженность поля между двумя равномерно и разноименно заряженными бесконечными параллельными плоскостями (поле плоского конденсатора)

.

• Связь потенциала с напряженностью:

а) в общем случае

, или ;

б) в случае однородного поля

,

где d – расстояние между точками с потенциалами ₁ и ₂, взятое вдоль электрической силовой линии;

в) в случае поля, обладающего центральной или осевой симметрией .

• Работа сил поля по перемещению заряда q из точки поля с потенциалом ₁ в точку с потенциалом ₂

, или ,

где Е_l – проекция вектора напряженности на направление перемещения;

dl – величина перемещения.

В случае однородного поля

,

где  – угол между направлением вектора и направлением перемещения.

• Электроемкость:

а) уединенного проводника

,

где  – потенциал проводника;

б) плоского конденсатора

, или ,

где U – разность потенциалов пластин конденсатора;

S – площадь пластины (одной) конденсатора;

d – расстояние между пластинами;

в) уединенной проводящей сферы (шара) радиуса R

.

• Электроемкость батареи конденсаторов:

а) при последовательном соединении

,

б) при параллельном соединении:

С = С₁ + С₂ + …….+ С_n ,

где n – число конденсаторов в батарее.

• Энергия заряженного конденсатора

.

• Объемная плотность энергии электрического поля

.

• Сила постоянного тока

, или .

• Плотность тока

,

где S – площадь поперечного сечения проводника.

• Закон Ома:

а) для однородного участка цепи, не содержащего ЭДС

,

где – разность потенциалов на концах участка цепи;

R – сопротивление участка;

б) для участка цепи, содержащего ЭДС

,

где  – ЭДС источника тока на данном участке;

в) для замкнутой (полной) цепи

,

где R – внешнее сопротивление цепи;

r – внутреннее сопротивление источника тока с ЭДС ;

г) в дифференциальной форме

,

где j – плотность тока;

 – удельная проводимость.

• Сопротивление R и проводимость  однородного проводника длиной l и площадью поперечного сечения S:

; ,

где  – удельное сопротивление проводника;

–удельная проводимость проводника.

• Общее сопротивление системы проводников:

а) – при последовательном соединении;

б) – при параллельном соединении,

где R_i – сопротивление i-го проводника.

• Законы Кирхгофа:

а) первый закон: ,

где – алгебраическая сумма токов, сходящихся в узле;

б) второй закон: ,

где – алгебраическая сумма произведений сил токов на сопротивления участков;

–алгебраическая сумма ЭДС, входящих в рассматриваемый замкнутый контур.

• Мощность тока: ; ;.

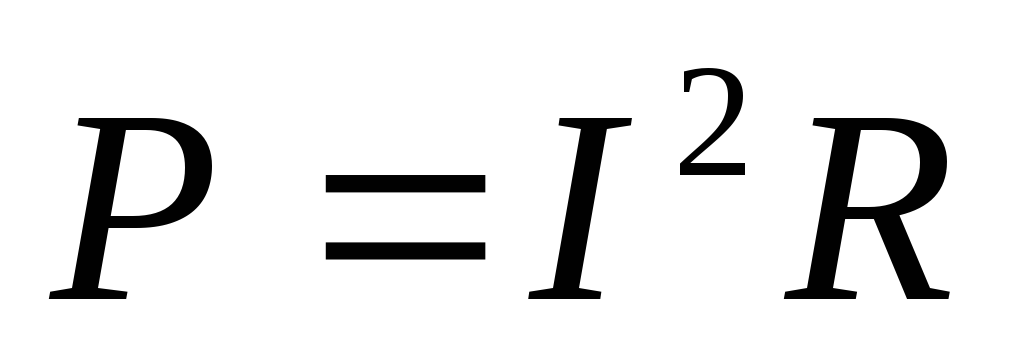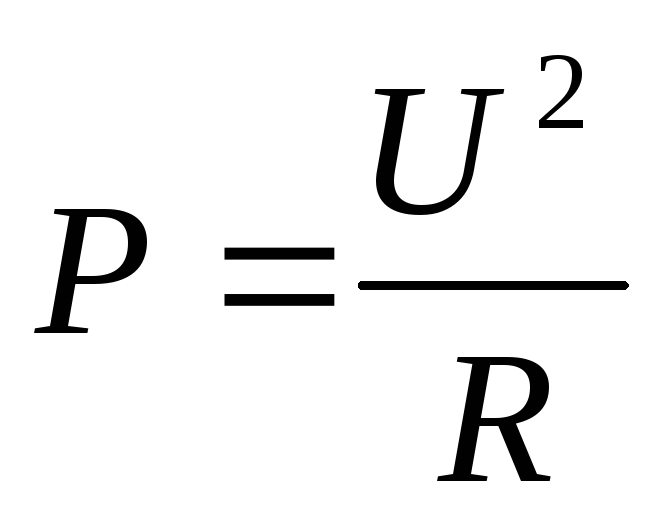• Закон Джоуля-Ленца (тепловое действие тока в проводнике сопротивлением R за время прохождения тока t)

.

• Полная мощность, выделяющаяся в замкнутой цепи

,

где  – ЭДС источника тока.

• Закон Био-Савара-Лапласа для элемента проводника с током

, или ,

где  – магнитная проницаемость изотропной среды;

₀ – магнитная постоянная (₀ = 410^-7 Гн/м);

–радиус-вектор, направленный от элемента проводника к точке, в которой определяется магнитная индукцияполя;

α – угол между радиусом-вектором и направлением тока в элементе провода.

• Магнитная индукция поля, созданного:

а) бесконечно длинным прямым проводником с током

,

где r₀ – расстояние от оси провода до точки, в которой определяется магнитная индукция;

б) в центре кругового витка с током

,

где R – радиус витка;

в) отрезком проводника с током

,

г) бесконечно длинным соленоидом на его оси (внутри соленоида)

,

где n – отношение числа витков соленоида к его длине.

• Связь магнитной индукции с напряженностьюмагнитного поля

.

• Сила действующая на прямой провод с током в однородном магнитном поле (закон Ампера)

, или ,

где l – длина провода;

 – угол между направлением тока в проводе и вектором магнитной индукции .

• Магнитный момент плоского контура с током I:

,

где – единичный вектор нормали к плоскости контура, направление которой определяется в соответствии с правилом буравчика;

S – площадь контура.

• Механический (вращательный) момент, действующий на контур с током, помещенный в однородное магнитное поле

,или ,

где α – угол между векторами и.

• Сила Лоренца

, или ,

где – скорость заряженной частицы;

α – угол между векторами и.

• Магнитный поток:

а) в случае однородного магнитного поля и плоской поверхности

, или ,

где S – площадь контура;

α – угол между нормалью к плоскости контура и вектором магнитной индукции;

б) в случае неоднородного поля и произвольной поверхности:

.

• Потокосцепление (полный поток)

.

• Работа по перемещению замкнутого контура с током в магнитном поле

.

• Основной закон электромагнитной индукции (закон Фарадея)

.

• ЭДС самоиндукции

.

• Индуктивность контура

.

• Индуктивность соленоида, имеющего N витков

, или ,

где – отношение числа витков соленоида к его длине;

–объем соленоида.

• Разность потенциалов на концах провода длиной l, движущегося со скоростью 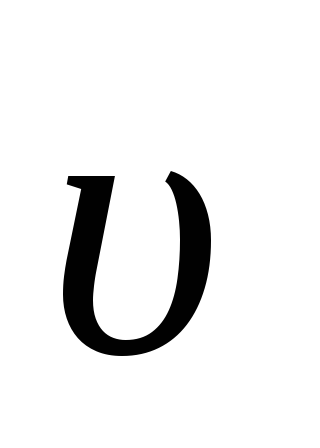в магнитном поле

,

где α - угол между векторами и.

• Энергия магнитного поля

.