Розв'язання прикладів
Приклад 1.
Провести
повне дослідження функції y=
і побудувати її графік за результатами
дослідження.
Розв'язання.
Задана функція визначена на всій
числовій осі, крім точки x=0.
Отже, в інтервалах (-∞;0) і (0;+∞) функція
неперервна, а x
=0 - точка
розриву функції. Функція не є ні парною,
ні непарною, бо y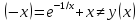
і y(-x)≠-y(x).
Отже, вона не симетрична.
Функція неперіодична.
Графік функції не перетинає вісь 0y, бо x≠0.
Розв'язуючи
рівняння e1/x
- x
=0 знаходимо точку перетину графіка з
віссю 0х:
Рис.19
рис. 20
Виходячи з дослідження, робимо висновок: для x є (-∞ ; 0) U(0;1,5) графік функції розміщений вище осі 0x, бо для цих x,y > 0, а для xє (1,5 +∞)
графік функції розміщений нижче осі 0х, оскільки для цих х ,у < 0. Далі досліджуємо функцію поблизу точок розриву і знаходимо асимптоти.
Як відзначалося вище, х=0 – точка розриву функції.
Отже,
х=0 – вертикальна
асимптота функції при
х
→ 0
Тепер знаходимо похилі асимптоти y = kx+b, де
k =
=
- 1=
- 1 = -1,
Таким чином,
похила
асимптота.
Оскількиγ
= e1/x
<0
для всіх х
із області
визначення, то функція монотонно спадає,
а тому екстремумів немає.
Знаходимо інтервали опуклості і вогнутості функції та точки перетину:
γ
=
якщо
звідки
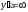при
Зауважимо, що при визначенні знака y´(x) (рис. 21) слід врахувати, що e1/x>0 , x4>0 для всіх значень х із області визначення функції.
y´(-1)<0,
y´(
)>0,y´(1)>0
Таким
чином, для xϵ(-∞;
),
крива є опуклою, а дляxϵ(-
;
0)U(0;
+∞) – вoгнутою.
У
перетину = е-2
+
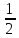≈0,6
при х= -
.
Нанісши на площину всі характерні точки функції у = е 1/x – х і використавши її згадані вище особливості, креслимо графік цієї функції (рис. 22)
Приклад
2. Провести повне дослідження функції
у =
,
побудувати її графік за результатами
дослідження.
Розв’язування. Слідуючи запропонованій схемі, маємо:
3 – x2 ≠ 0; x ≠ ±
;
D(y)
= (-∞;-
)
U (-
;
)
U (
;
+∞)
x = -
x
=
– точки розриву.
(−
∞; -
),
( -
;
)
і (
+ ∞)
– інтервал неперервності функції.
y(-x) =
=
= - у(x),
Отже, у(x) – функція непарна. Її графік розташований симетрично відносно початку координат, тому подальші дослідження досить проводити лише для x≥0,
Рис.21
∞ 0 Y інтервал
знакосталості
0 1,5 Х
Y 
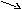
∞ Y´ інтервал
монотонності
X
перетин 
0 ∞ Y´ опуклий
увігнутий
0,5 0 X
Рис.22
4. При х = 0, у = 0, при у = 0, х = 0, тобто графік функції проходить через точку О (0 ; 0) – початок координат.
5.
у = 0 при х = 0 , у = ∞ при х =
у >0 в інтервалі (0;
)
і у < 0 в інтервалі (
∞)
(рис.23)
6.
х =
- точка розриву функції.
;
-
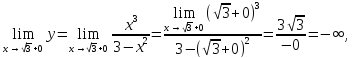
вертикальна
асимптота.
Знаходимо
похилі асимптоти у
= кх+в,
де
к
=
Оскільки
степені многочленів чисельника і
знаменника однакові:
в
=
Оскільки степінь многочлена чисельника менша степені многочлена знаменника. Отже, у = -х – похила асимптота.
7.
якщо
;
(рис.24)
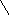
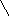
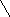
0
3
∞
екстр. немає
0
точка розриву
∞
0
max
+
+
+
-
y
Рис.24
8.y
Зауважимо,
що у зв’язку з тим, що точка х = 0 знаходиться
на межі пів інтервалу [0;+ ∞], в якому
досліджується функція, виникла
необхідність дослідити знак y′ і y
на пів інтервалі (
;0].
9.Будуємо графік функції за результатами дослідження (рис. 26).
Приклад
3. Провести
повне дослідження функції
і побудувати її графік за результатами
дослідження.
Розв’язання.
1.
-1
≠ 0, звідки х ≠ ±1;
D(y)
= (-∞;-1)
(-1;1)
(1;
∞).
2. В інтервалах (- ∞;-1), (-1;1) і (1; ∞) функція неперервана, х = -1 і х = 1 – точки розриву функції.
3.
у(-х) =
=
= у(х), отже, у(х) – парна функція,її графік
розташований симетрично відносно осі
Оу, тому досить провести подальше
дослідження лише для х ≥ 0.
4. При х = 0, у = 0, при у = 0, х = 0,тобто графік функції проходить через початок координат.
5. у = 0 при х = 0, у = ∞ при х = ±1;
y
< 0 для
х
(0;1) і у>
0 для х
(1;
∞)(рис. 27).
6. х = 1 – точка розриву функції.
.
.
Х = 1 – вертикальна асимптота.
Рис.26
Оскільки
k
=
=
=
=
=0,
=1,
то
пряма
,
тобто у –1
– горизонтальна асимптота.
7.
=
=
=
;
уˈ = 0, якщо х = 0 ;
уˈ = ∞, якщо х = ± 1 ;
при х = 0 (рис.
28).
8.уˈ=
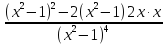= -2
=
-2
.
уˈ≠ 0;
уˈ= ∞ при х = ± 1.
Результати дослідження зображені на ( рис. 29)
9.
Будуємо
графік функції (рис.
30)
за результатами дослідження ± додатковими
точками
(Дивись
зауваження до попереднього прикладу.)