Розв’язання прикладів

Приклад 1. Показати , що графік функції y= xarctgx всюди вoгнутий.

Розв’язання. Задана функція визначена на всій числовій осі. Знайдемо першу і другу похідні:

;

)=+=+==;

При будь-яких х, уʹ >0, а це означає,що графік даної функції всюди вогнутий.

Приклад 2. Знайти інтервали опуклості і вогнутості на точках перетину графіка функції y = x³ - 5x²+3x-5.

Розв’язання.

1.Функція визначена для всіх

2.yʹ(x)=3x² -10x+3.

3.yʹ(x)=6x - 10=2(3x-5).

4.yʹ(x)=0, якщо 3х-5=0, звідки , уʹ(х) ≠ ∞.

5.Для х, уʹ(х) <0 бо, наприклад уʹ(0)= -10 < 0,отже, в інтервалі крива є опуклою, а в інтервалі – вoгнутою.

6.В точці друга похідна даної функції дорівнює 0 і при переході через точку змінює знак,а це означає, щов точки перегину кривої.

7.Обчислюємо значення функції при, одержуємо у= Таким чином, М (- точка перегину графіка даної функції.

Приклад 3. Знайти інтервали опуклості і вoгнутості та точки перетину функції у=ln (1+x²).Розв’язання. Задана функція визначена на всій числовій осі, оскільки 1+х² для всіх Диференціюючи її двічі, одержимо 12x.

;

ⁿ =2=.

Друга похідна існує на всій числовій осі і обертається в нуль при x = -1 і x = 1 . Ці точки розбивають область визначення функції на три інтервали, в кожному із яких похідна ⁿ=(x) оберігає знак. Визначаючи знак другої похідної в довільно взятій точці кожного інтервалу, одержимо:

ⁿ (-2)<0, ⁿ (0)>0, ⁿ(2)<0.

При визначенні знака другої похідної слід врахувати, що знаменник при всіх значеннях x.

Обчислюючи значення функції при x = ± 1; знаходимо (-1)=(1)=

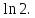
Таким чином, графік функції = є опуклим в інтервалах

(-∞;1) та (1;+∞) і вогнутим . Крива має дві точки перетину (-1; і(1 ;.

Питання для самоперевірки

1. Яка крива називається опуклою ( вогнутою)?

2. В чому полягає достатня умова існування інтервалів опуклості (вогнутості) кривої?

3. Що називається точкою перегину графіка функції?

4. Сформулюйте необхідну і достатню умови існування точки перетину кривої.

Вправи

1. Показати що графік функції всюди опуклий.

2. Знайти інтервали опуклості і вогнутості кривої ^x.

Відповідь: в інтервалі (-∞ ; -2) крива опукла, а в інтервалі (-2;+∞) -вoгнута.

3. Знайти точку перегину кривої y = (x – 1)⁶ .

Відповідь: M (1; 0).

4. Знайти інтервали опуклості і вгнутості та точки перетину графіка функції y=

Відповідь: точок перегину немає, графік функції вoгнутий.

5. Знайти інтервали опуклості і вогнутості та точки перегину кривої y=

Відповідь: в інтервалі [0; 1] крива опукла, а в інтервалі (1;+∞) – вогнута.

Точка перетину [1; -7].

8. Повне дослідження функції і побудова графіка

Повне дослідження функції рекомендується проводити за такою схемою:

1. Знайти область визначення функції.

2. Встановити точку розриву, та інтервали неперервності функції.

3. Дослідити функцію на парність і непарність.

4. Знайти точки перетину графіка функції з осями координат.

5. Знайти інтервали знакосталості функції.

6. Знайти асимптоти. Дослідити поведінку функції поблизу точок розриву.

7. Знайти інтервали опадання і зростання функції та eкстремуми.

8. Знайти інтервали опуклості і вогнутості графіка функції та точки перетину.

9. Побудувати графік функції за результами дослідження.

Зробимо кілька зауважень щодо цієї схеми.

1.Якщо функція виявиться парною або непарною, то дослідження досить провести лише для невід’ємних значень аргументу, а потім скористатися властивістю симетрії.

Якщо в результаті дослідження виявиться , що функція періодична, то наступне дослідження цієї функції досить провести на відрізку довжиною в період. З’ясувавши всі особливості функції в цьому відрізку, встановимо (внаслідок періодичності) її особливості в усій області існування.

2. Доцільно наносити на рисунок характерні точки , асимптоти і т.п

паралельно з дослідженням. Це скоротить роботу з накресленням графіка.

3. Щоб як умога точніше накреслити графік функції в тих інтервалах області її існування, в яких немає особливостей цієї функції і які великі за розмірами, треба взяти кілька точок і обчислити значення функції в цих точках.