6.Інтервали монотонності і екстремуми функції. Найменше і найбільше значення функції на відрізку
6.1.Інтервали зростання і опадання функції
Кажуть,
що функція
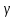= f(x)
на
інтервалі (a;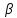
)<D(
)
зростає (спадає), якщо для будь-яких двох
значень аргументу x1,
x2
є (a;b)
із умови x2>
x1
випливає, що f
(x2)>f(x1)
(f(x2)<f(x1)).
Щоб знайти інтервали зростання та спадання функції, треба дослідити знак різниці f(x2) - f(x1) за умови, що x2 > x1 .
Якщо
ця різниця на певному інтервалі додатна,
то
функція
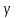= f(x)
на такому інтервалі зростає,
якщо
ж різниця
f(x2)
-
f(x1
)
від’ємна,
то функція
спадає.
Інтервали, на яких функція лише зростає або лише опадає, називають інтервалами монотонності функції.
Зрозуміло, що встановити безпосередньо знак різниці f(x2) – f(x1) не завжди легко, а тому при дослідженні функції на монотонність найчастіше використовують похідну функції.
Функції, з якими ми матимемо справу, мають ту властивість, що їхню область визначення можна поділити на проміжки, в кожному з яких функція диференційована. Для таких функцій відшукання проміжків монотонності зводиться до дослідження на знак їхніх похідних.
Зауважимо, що відрізок [a ; b], інтервал (a ; b), пів-інтервали або пів-відрізки (a ; b] і [a ; b) називають проміжками і позначають <a ; b>.
Для
того, щоб неперервна на проміжку <
a
; b
>
і диференційована в інтервалі (a
; b)
функція f(x)
була зростаючою(спадною) на проміжку<a
; b>,
необхідно й достатньо, щоб f′(x)≥0
(f
′(x)≤0)
для
всіх x
(a ;b).
Зауважимо, що похідна зростаючої (спадної) функції може обертатись в нуль в деяких точках . Наприклад, функція f(x)=x 3 зростає в інтервалі
(- ∞;+∞), однак її похідна f′ (x)=3x2 дорівнює нулю в точці x = 0.
Якщо ж
f′(x)
> 0 (f
′(x)
<0)
для всіх x
(a
; b)
,то в інтервалі (a
; b)
функція y
=f(x)
зростає (спадає).
6.2.Екстремуми функції
Вважають ,що функція f(x) в точці x 0 має максимум (мінімум) , якщо існує окіл ( x0 – δ ; x0 + δ0 ) цієї точки такий , що для всіх xє( x0 – δ ; x0 + δ ), x≠x0 виконується нерівність f(x) < f(x0) ( f(x) > f(x0) ).
Максимум і мінімум функції в точці називають екстремумом цієї функції в цій точці. Екстремум функції в точці іноді називають локальним (місцевим) екстремумом цієї функції в цій точці. Слово «локальний» (місцевий) має на меті підкреслити, що значення функції в точці x0 є найбільшим (найменшим) порівняно не з усіма значеннями цієї функції в області її існування, а з тими її значеннями, яких вона набуває в точках, що лежать у досить малому околі точки x0 і відмінні від точки x0 .
Якщо функція f(x) в точці x0 має екстремум ( максимум або мінімум), то похідна функції в цій точці дорівнює нулю або не існує ( необхідна умова існування екстремуму).
Точка x 0 називається критичною точкою першого роду, або просто критичною, якщо має місце одна із умов :
f ′ (x0) = 0;
f ′ (x0) = ∞;
Функція f(x) в точці x0 визначена , але f ′(x0) не існує.
Геометрично ці умови означають, що в критичній точці дотична або паралельна осі 0x , якщо виконується умова 2 , або дотичної зовсім не існує ( рис. 11 ) , якщо має місце умова 3. Точки , в яких похідна дорівнює нулю , називають стаціонарними .
Не кожна критична точка функції є точкою екстремуму цієї функції . Так, з рис.11 видно, що точки x1 , x2 , x3 , x4 , x6 , x7 і x9 є екстремальними, причому в точках x1 , x3 , x6 і x9 функція y = f(x) має максимум, а в точках x2 , x4 і x7 – мінімум. Що стосується точок x0 , x5 , x8, то жодна із
цих точок не є точкою екстремуму.
Якщо при переході ( зліва направо ) через критичну точку x0 похідна f(x) змінює знак з плюса на мінус, то в точці x0 функція f(x) має максимум, а якщо з мінуса на плюс, то мінімум; якщо ж знака не змінює, то екстремуму немає ( достатня умова існування екстремуму ) .
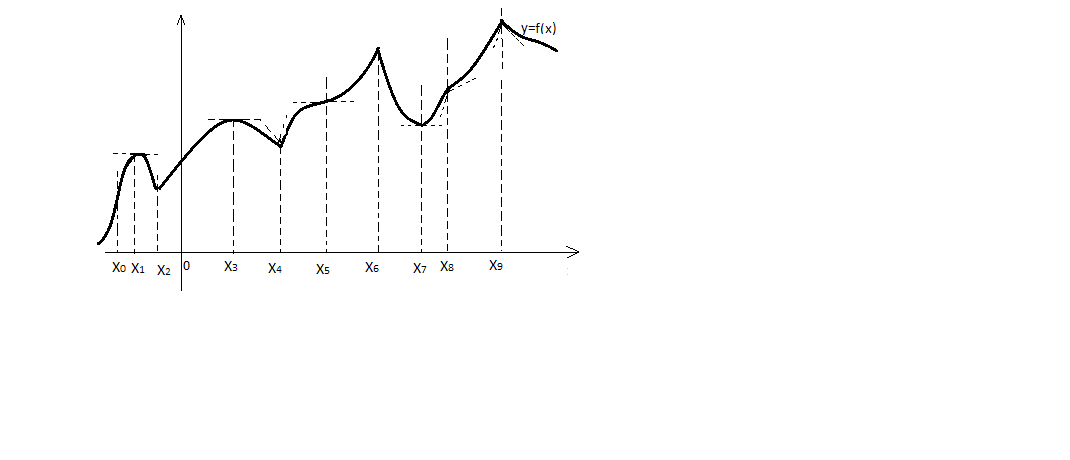
Рис. 11
При знаходженні інтервалів монотонності і екстремумів функції доцільно
керуватися правилом, яке випливає із указаного вище:
1) знаходимо область визначення функції;
2) знаходимо f ′(х);
3) знаходимо корені рівняння f ′(x)=0 f ′(x);
4) розставляємо одержані точки на числовій осі в порядку зростання;
5) визначаємо знак f ′(x) в кожному із одержаних інтервалів, для цього слід похідну розкласти на множники, якщо це можливо, і тим самим знаходимо інтервали спадання і зростання функції;
6) визначаємо, які із критичних точок є екстремальними ( рис. 12).
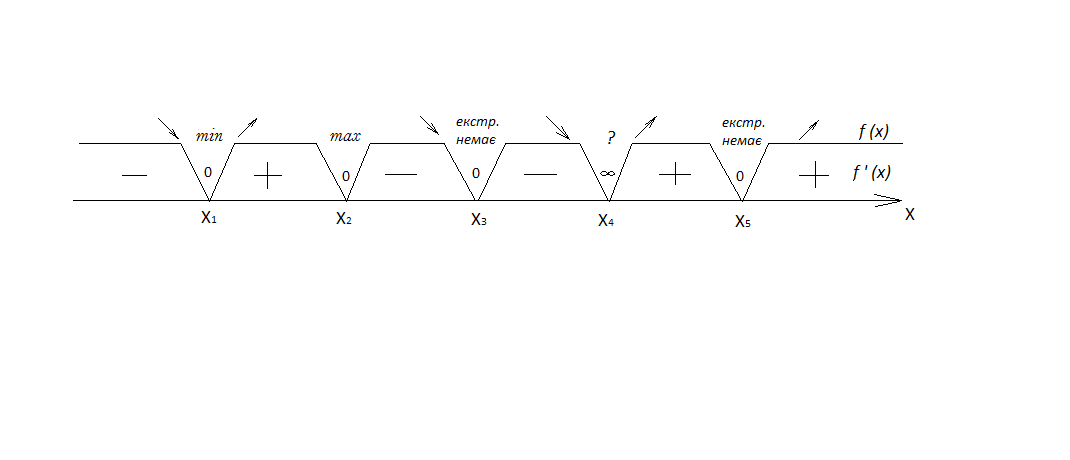
Рис. 12
Зауважимо, що в точці x4 функція має min, якщо f(x) в цій точці
визначена, або в точці x4 екстремуму немає, якщо f(x) в цій точці не визначена;
7) обчислюємо значення функції в екстремальних точках, тобто знаходимо шукані екстремуми.