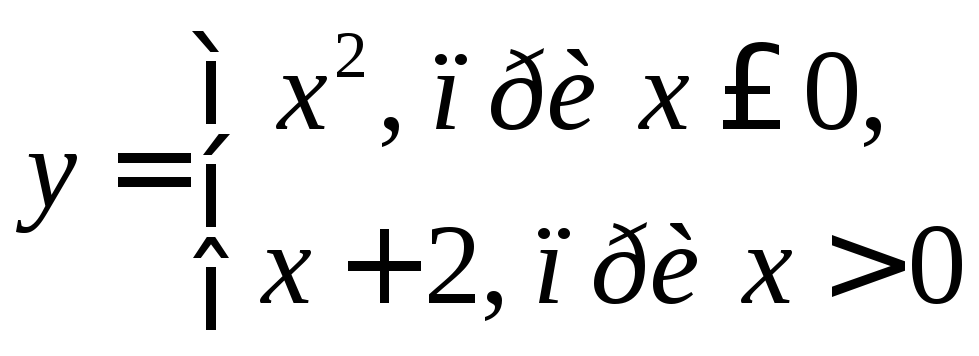Теория пределов

1. Функция

1.1. Понятие функции

Определение. Если каждому значению переменной х, принадлежащему некоторой области, по некоторому правилу или закону ставится в соответствие одно определенное значение другой переменной у, то у называется зависимой переменной или функцией от независимой переменной (аргумента) х.

Символическая запись функции: у=f(x), у=y(x), у=(x), у=F(x) и т.д. Символами f, y, , F,... в этих равенствах обозначается именно закон соответствия.

Область изменения аргумента х называется областью определения функции, а множество значений у называется областью изменения функции.

Будем обозначать область определения функции D(f), а область изменения функции E(f).

Из приведенного определения следует, что функция считается заданной, если:

а) известна область определения функции;

б) указано правило или закон по которому каждому значению аргумента х ставится в соответствие одно определенное значение у.

Примеры функций

у=2х+1

1.2. Классификация функций

а) Основные элементарные функции.

• Степенная функция у=x^где – действительное число.

• Показательная функция у=а^хгде а – любое положительное число, отличное от единицы: а>0; а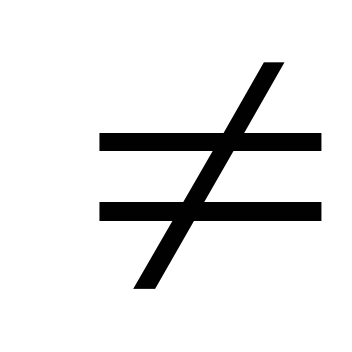1.

• Логарифмическая функция у=log_ax, где а – любое положительное число, отличное от единицы: а>0; а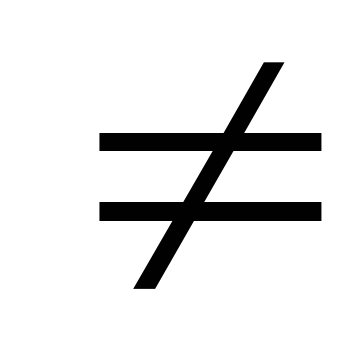1.

• Тригонометрические функции y=sin x, y=cos x, y=tg x, y=ctg x.

• Обратные тригонометрические функции y=arcsinx, y=arccosx, y=arctgx, y=arcctg x.

Рассмотрим области определения и графики некоторых основных элементарных функций.

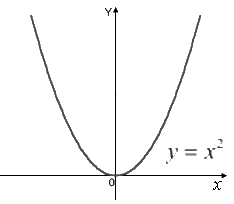
Степенная функция у=x^

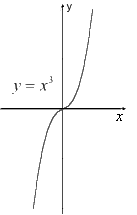
Графики функций при некоторых значениях имеют вид

 – целое положительное число. Функция определена в бесконечном интервале: .

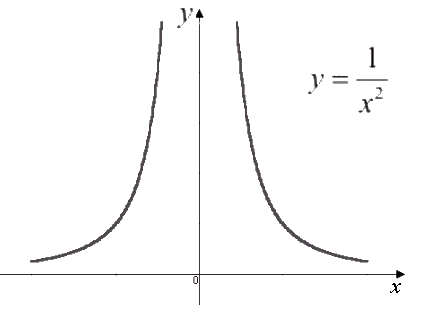
 – целое отрицательное число. В этом случае функция определена при всех значениях х, кроме х=0, .

Графики функций в этом случае при некоторых значениях имеют вид

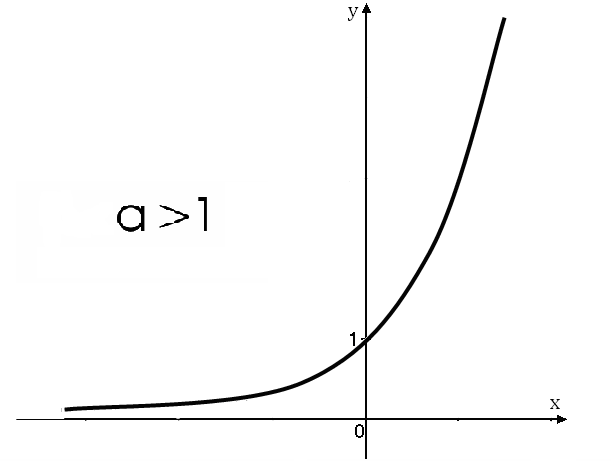
Показательная функция у=а^ха>0, а1.

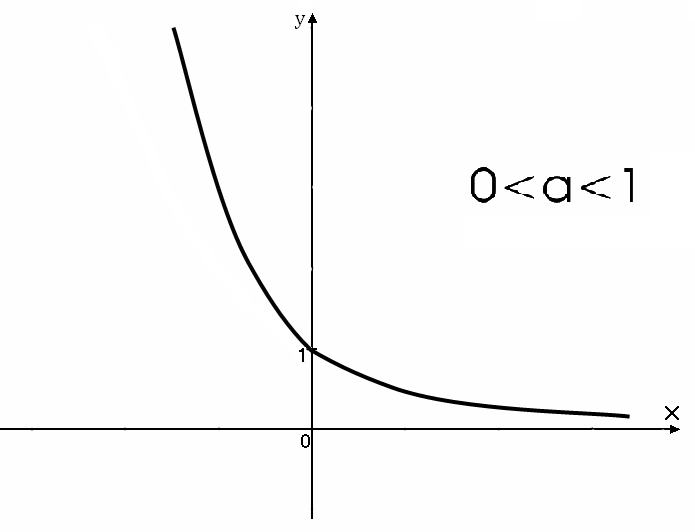
Функция определена при всех значениях х, т.е. . График функцииимеетвид

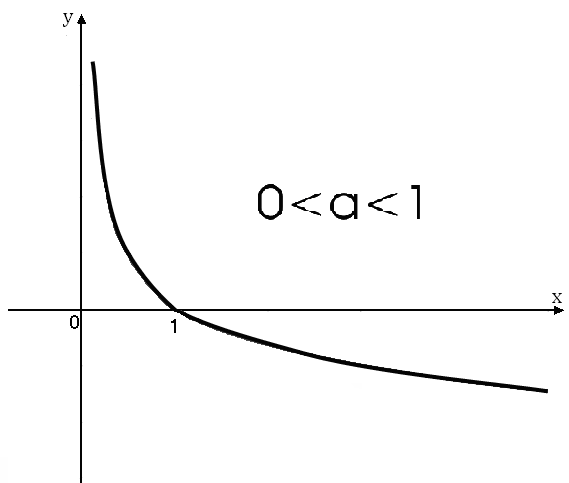
Логарифмическая функция у=log_ax, а>0, а1.

Функция определена при х>0, . График функцииимеет вид:

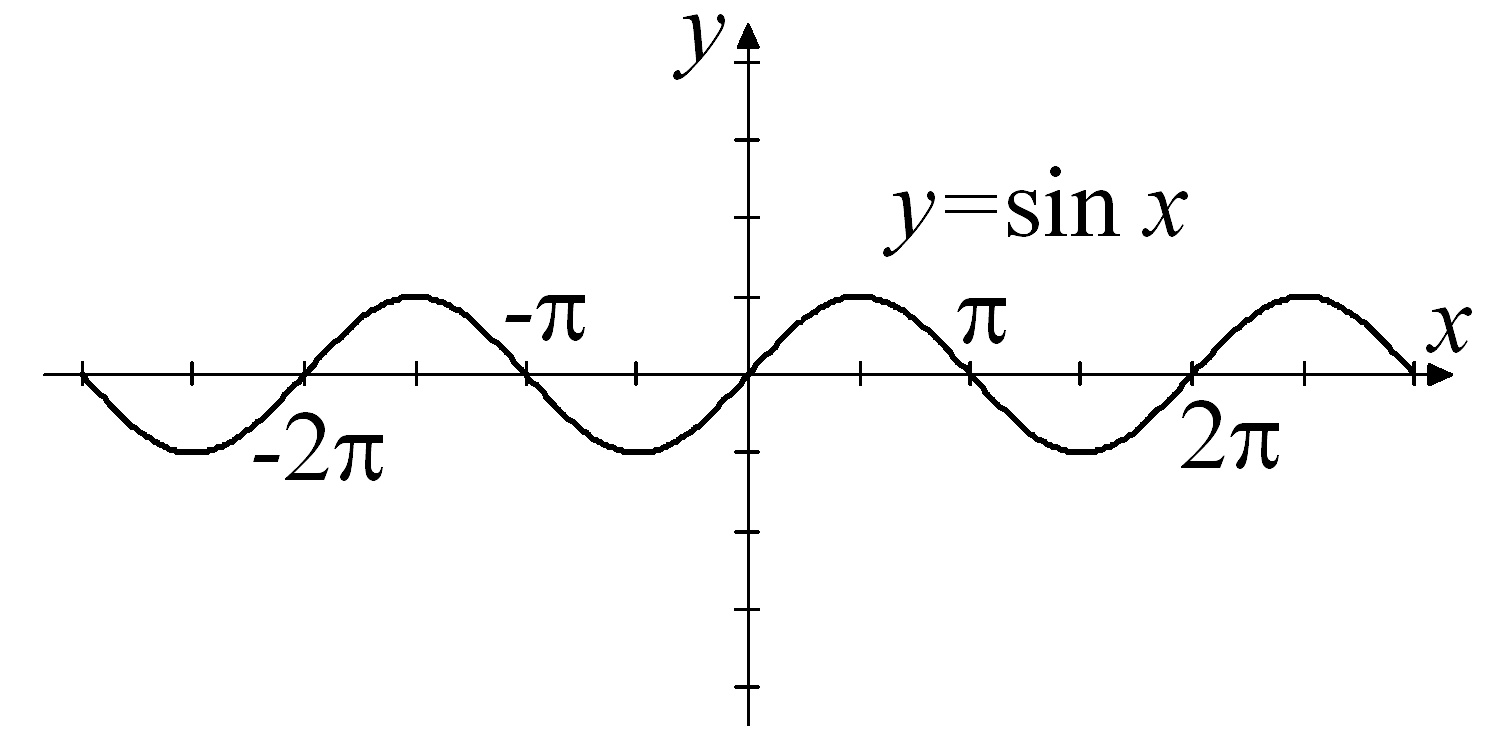
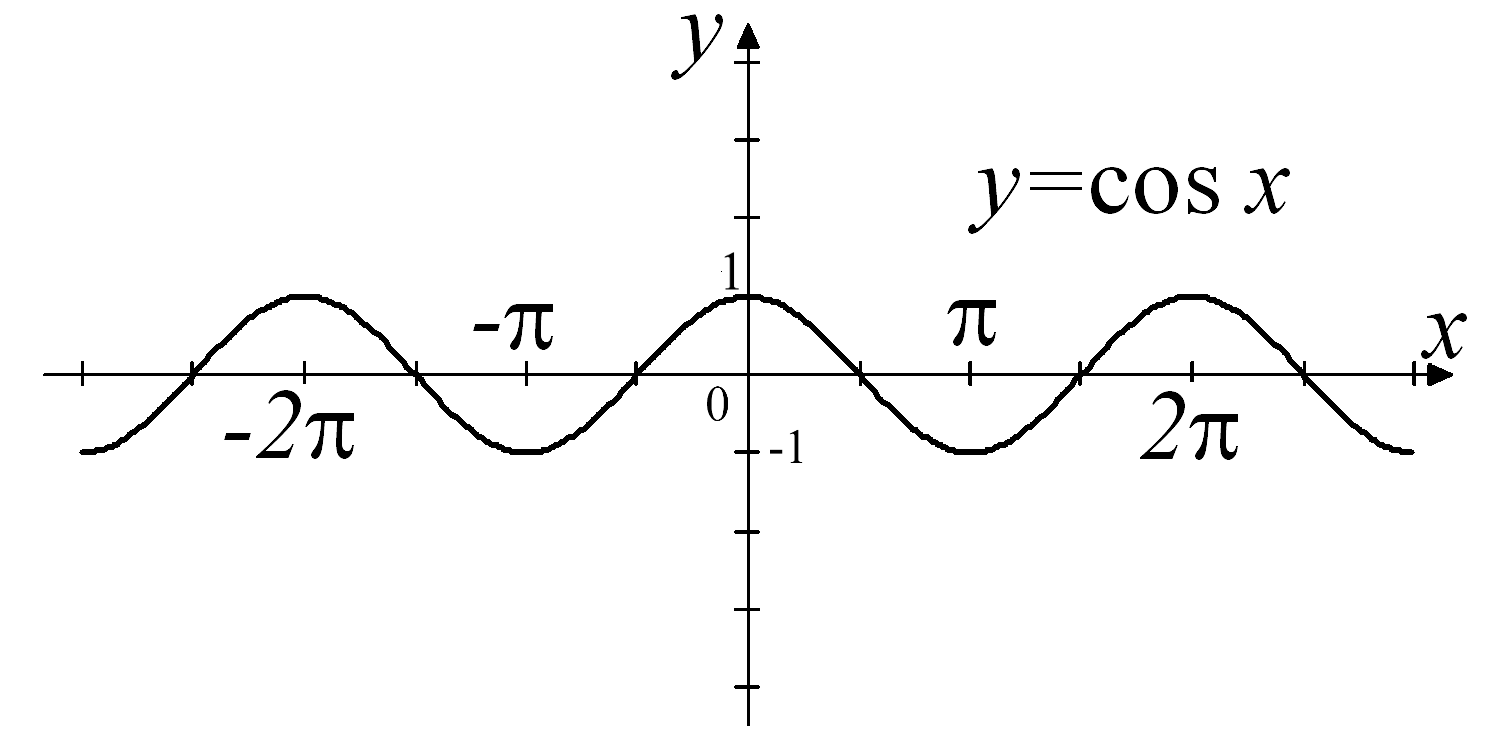
Тригонометрические функции y=sin x, y=cos x ,y=tg x, y=ctg x.

Независимая переменная х выражается в радианах. Функции y=sin x, y=cos x определены при всех значениях х, .

Функция y=tgx определена всюду, кроме точек х=(2k+1), .,.

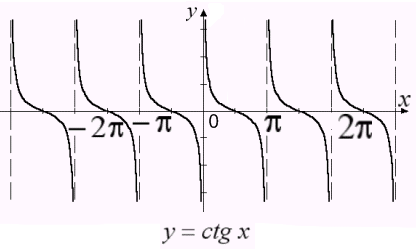
Функция y=ctgx определена всюду, кроме точек х=k, .,.

Обратные тригонометрические функции

Функция y=arcsin x определена для х, принадлежащему интервалу [–1,1], т.е. .

График имеет вид

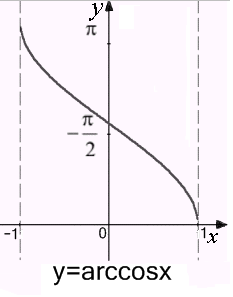
Функция y=arcсоs x определена для х, принадлежащему интервалу [–1,1]: .

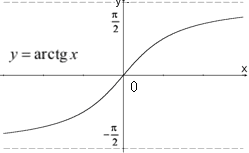
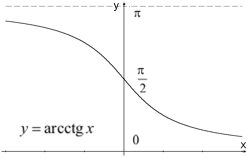
Функции y=arctgx, y=arсctgx, определены в бесконечном интервале, .

Графики имеют вид

б) Элементарные функции.

К элементарным функциям относят функции, получаемые из основных элементарных функций с помощью конечного числа арифметических действий (сложение, вычитание, умножение, деление) и суперпозиции (наложение) функций.

у=х²-5х+6, у=ln sin x, y=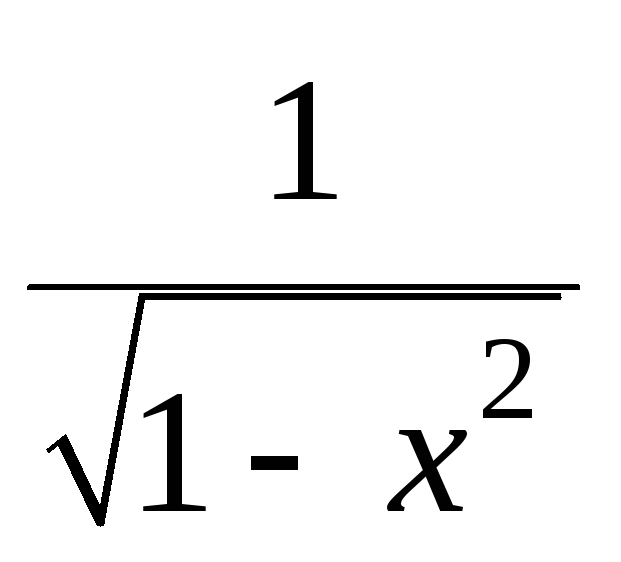.