
- •Методические указания по выполнению контрольной работы «Линейная алгебра»
- •Задания для контрольной работы по «Линейной алгебре» Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 6
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •Вариант 13
- •Вариант 14
- •Вариант 15
- •Вариант 16
- •Вариант 17
- •Вариант 18
- •Вариант 19
- •Вариант 20
- •Вариант 21
- •Вариант 22
- •Вариант 23
Задания для контрольной работы по «Линейной алгебре» Вариант 1
Показать, что векторы
 ,
, ,
, и
и образуют
базис пространства
образуют
базис пространства ,
и найти координаты вектора
,
и найти координаты вектора в
этом базисе.
в
этом базисе.Вектор
 задан в базисе
задан в базисе .
Найти его координаты в базисе
.
Найти его координаты в базисе ,
если
,
если
Матрица
 задана в базисе
задана в базисе .
Найти ее в базисе
.
Найти ее в базисе ,
, ,
, .
.Найти собственные значения и собственные векторы линейного преобразования, заданного матрицей
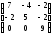 .
.
Структурная матрица торговли трех стран
 имеет вид
имеет вид .
Найти национальные доходы стран для
сбалансированной торговли.
.
Найти национальные доходы стран для
сбалансированной торговли.Записать матрицу квадратичной формы и найти ортогональное преобразование, приводящее квадратичную форму к каноническому виду и записать соответствующий канонический вид квадратичной формы:
 ;
;
Вариант 2
Показать, что векторы
 ,
, и
и образуют базис пространства
образуют базис пространства ,
и найти координаты вектора
,
и найти координаты вектора в
этом базисе.
в
этом базисе.Вектор
 задан в базисе
задан в базисе .
Найти его координаты в базисе
.
Найти его координаты в базисе если
если
Матрица
 задана в базисе
задана в базисе .
Найти ее в базисе
.
Найти ее в базисе ,
, ,
, .
.Найти собственные значения и собственные векторы линейного преобразования, заданного матрицей
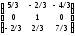 .
.Структурная матрица торговли четырех стран
 имеет вид
имеет вид
 .
.
Найти национальные доходы стран для сбалансированной торговли.
Записать матрицу квадратичной формы и найти ортогональное преобразование, приводящее квадратичную форму к каноническому виду и записать соответствующий канонический вид квадратичной формы:
 ;
;
Вариант 3
Показать, что векторы
 ,
, ,
, и
и образуют
базис пространства
образуют
базис пространства ,
и найти координаты вектора
,
и найти координаты вектора в
этом базисе.
в
этом базисе.Вектор
 задан в базисе
задан в базисе .
Найти его координаты в базисе
.
Найти его координаты в базисе ,
если
,
если
Матрица
 задана в базисе
задана в базисе .
Найти ее в базисе
.
Найти ее в базисе ,
, ,
,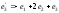 .
.Найти собственные значения и собственные векторы линейного преобразования, заданного матрицей
 .
.Для откорма животных на ферме в ежедневный рацион каждого животного включается 6 ед. питательного вещества A и 7 ед. питательного вещества B. При этом используются корма K1, K2 и K3. Данные о содержании питательных веществ в одной весовой единице корма и ее стоимости приведены в следующей таблице:
|
Корм |
Содержание пит.вещества |
Стоимость ед.корма (ден.ед.) | |
|
A |
B | ||
|
K1 |
2 |
1 |
5 |
|
K2 |
1 |
2 |
1 |
|
K3 |
3 |
1,5 |
3 |
Определить состав еженедельного рациона для откорма животных стоимостью в 7 ден.ед., содержащего норму питательных веществ.
Записать матрицу квадратичной формы и найти ортогональное преобразование, приводящее квадратичную форму к каноническому виду и записать соответствующий канонический вид квадратичной формы:
 ;
;
.
.
Вариант 4
Показать, что векторы
 ,
, ,
, и
и образуют
базис пространства
образуют
базис пространства ,
и найти координаты вектора
,
и найти координаты вектора в
этом базисе.
в
этом базисе.Вектор
 задан в базисе
задан в базисе .
Найти его координаты в базисе
.
Найти его координаты в базисе ,
если
,
если
Матрица
 задана в базисе
задана в базисе .
Найти ее в базисе
.
Найти ее в базисе ,
, ,
, .
.Найти собственные значения и собственные векторы линейного преобразования, заданного матрицей
 .
.Структурная матрица торговли четырех стран
 имеет вид
имеет вид
 .
Найти национальные доходы стран для
сбалансированной торговли.
.
Найти национальные доходы стран для
сбалансированной торговли.Записать матрицу квадратичной формы и найти ортогональное преобразование, приводящее квадратичную форму к каноническому виду и записать соответствующий канонический вид квадратичной формы:
 ;
;
Вариант 5
Показать, что векторы
 ,
, и
и образуют базис пространства
образуют базис пространства ,
и найти координаты вектора
,
и найти координаты вектора в этом базисе.
в этом базисе.Вектор
 задан в базисе
задан в базисе .
Найти его координаты в базисе
.
Найти его координаты в базисе ,
если
,
если
Матрица
 задана в базисе
задана в базисе .
Найти ее в базисе
.
Найти ее в базисе ,
, ,
, .
.Найти собственные значения и собственные векторы линейного преобразования, заданного матрицей
 .
.Химическое предприятие состоит из трех цехов, выпускающих одинаковую продукцию. Расходные коэффициенты aij – количество единиц продукции i-го цеха, используемые как «сырье» для выпуска единицы продукции j-го цеха, заданы матрицей A. Количество единиц продукции i-го цеха, предназначенных для реализации (конечный продукт), задается матрицей Y. Определить: 1) валовой выпуск (план) для каждого цеха; 2) производственную программу цехов.
 ,
, .
.Записать матрицу квадратичной формы и найти ортогональное преобразование, приводящее квадратичную форму к каноническому виду и записать соответствующий канонический вид квадратичной формы:
 ;
;
