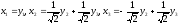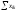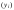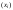- •Методические указания по выполнению контрольной работы «Линейная алгебра»
- •Задания для контрольной работы по «Линейной алгебре» Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 6
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •Вариант 13
- •Вариант 14
- •Вариант 15
- •Вариант 16
- •Вариант 17
- •Вариант 18
- •Вариант 19
- •Вариант 20
- •Вариант 21
- •Вариант 22
- •Вариант 23
Методические указания по выполнению контрольной работы «Линейная алгебра»
Пример
1. Даны
четыре вектора
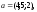
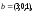
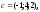
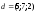 в некотором базисе. Показать, что векторы
в некотором базисе. Показать, что векторы тоже образуют базис и найти координаты
вектора
тоже образуют базис и найти координаты
вектора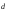 в этом базисе.
в этом базисе.
Решение.
Сначала покажем, что векторы
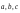 образуют базис. Исходя из определения
базиса, надо показать, что эти векторы
являются линейно независимыми. Это
можно сделать двумя способами.
образуют базис. Исходя из определения
базиса, надо показать, что эти векторы
являются линейно независимыми. Это
можно сделать двумя способами.
1 способ. Составим
нулевую линейную комбинацию векторов
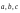 и
и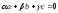 ,
найдем коэффициенты
,
найдем коэффициенты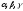 этой комбинации.
этой комбинации.
Запишем это равенство в координатной форме
 .
.
Используя операции умножения вектора на число и равенство векторов, получим систему уравнений:
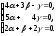
Решим эту систему, например, методом Гаусса:


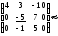
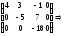
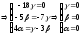 .
.
Значит,
нулевая линейная комбинация векторов
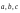 имеет место, когда
имеет место, когда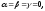 а это значит, что эти векторы линейно
независимы, а потому образуют базис.
а это значит, что эти векторы линейно
независимы, а потому образуют базис.
2 способ. Найдем
ранг системы векторов
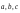 .
Для этого составим матрицу, столбцами
(или все равно что строками) которой
будут координаты заданных векторов, и
найдем ее ранг, например, методом
элементарных преобразований.
.
Для этого составим матрицу, столбцами
(или все равно что строками) которой
будут координаты заданных векторов, и
найдем ее ранг, например, методом
элементарных преобразований.
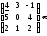
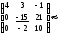
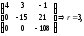
т.к. матрица приведена к треугольной форме и в ней осталось три ненулевых строки. Так как ранг системы из трех векторов равен трем, то система линейно независима и, значит, образует базис трехмерного векторного пространства.
Теперь найдем
координаты вектора
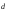 в базисе
в базисе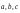 .
Для этого разложим вектор
.
Для этого разложим вектор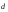 по базису
по базису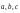 :
:
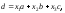
где
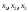 – координаты вектора
– координаты вектора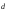 в новом базисе
в новом базисе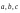 .
.
Последнее равенство запишем в координатной форме
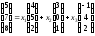 .
.
Отсюда получаем следующую систему уравнений:
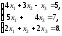
Решим систему, например, методом Гаусса:


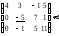
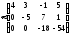

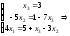
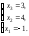
Таким
образом, в базисе
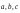 :
: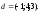
Пример
2. Вектор
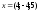 задан в базисе
задан в базисе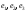 .
Найти его координаты в базисе
.
Найти его координаты в базисе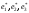 ,
если
,
если
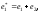
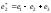 ,
,
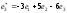 .
.
Решение.
Матрицу перехода от базиса
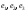 к базису
к базису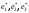 найдем по формуле (1); она имеет вид
найдем по формуле (1); она имеет вид .
Найдем матрицу
.
Найдем матрицу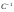 .
.
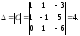
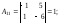
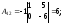
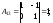
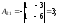
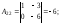
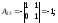
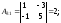
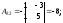
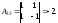
 .
.
Используя формулу (2), найдем
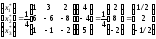 .
.
Таким
образом,
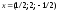 .
.
Пример
3. Матрица
 линейного оператора
линейного оператора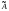 задана в базисе
задана в базисе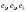 .
Найти ее в базисе
.
Найти ее в базисе
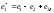
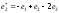 ,
,
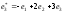
 .
.
Решение.
По формуле (1) найдем матрицу
 перехода от старого к новому базису:
перехода от старого к новому базису: .
.
Найдем
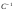 .
.
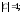
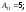
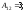

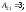
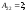
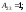
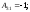
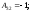
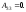
Следовательно,
 .
.
По формуле (4) найдем
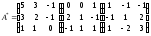 =
=

Пример 12. Найти собственные значения и собственные векторы линейного преобразования (оператора), заданного матрицей
 .
.
Решение.
Составим
характеристическое уравнение по формуле
(6), т.е.
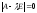 .
.

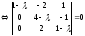 .
.
Решим это уравнение, найдя определитель.
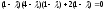 ,
,
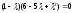
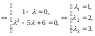
Собственные
значения
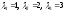 найдены.
найдены.
Найдем собственный
вектор
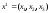 ,
соответствующий собственному значению
,
соответствующий собственному значению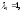 используя формулу (7):
используя формулу (7):
 .
.
Из этого равенства получим систему уравнений:
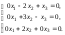
Решим эту систему методом Гаусса:



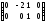 .
.
Следовательно,
ранг системы уравнений равен 2, т.е. число
базисных неизвестных 2. А так как число
неизвестных системы равно 3, то число
свободных неизвестных равно 1. Система
имеет бесчисленное множество решений.
Базисный минор
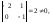 т.е.
т.е. и
и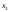 – базисные переменные,
– базисные переменные,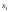 – свободная.
– свободная.
Таким
образом,
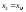
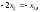
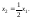 Пусть
Пусть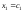 ,
где
,
где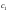 – любое не равное нулю действительное
число. Тогда
– любое не равное нулю действительное
число. Тогда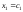 ,
,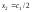 ,
,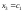 .
Значит,
.
Значит,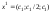 ,
где
,
где – собственный вектор, соответствующий
собственному значению
– собственный вектор, соответствующий
собственному значению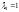 .
.
Найдем собственный
вектор
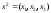 ,
соответствующий собственному значению
,
соответствующий собственному значению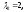 используя формулу (7). Получим систему
уравнений:
используя формулу (7). Получим систему
уравнений:
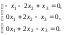
Применим гауссовские преобразования:
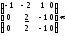
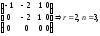
т.е.
две переменные базисные, а одна –
свободная. Базисный минор
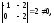 поэтому
поэтому
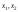 – базисные, а
– базисные, а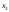 – свободная переменная.
– свободная переменная.
Таким образом,
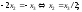
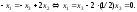
Полагая
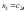 где
где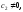 но любое действительное число, получим
но любое действительное число, получим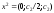 – собственный вектор, соответствующий
собственному значению
– собственный вектор, соответствующий
собственному значению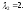
Найдем собственный
вектор
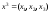 ,
соответствующий
,
соответствующий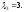
Получим систему уравнений:
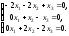
Решим ее методом Гаусса:
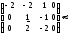
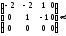
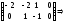

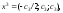
где
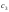 – любое, не равное нулю, действительное
число.
– любое, не равное нулю, действительное
число.
Пример 4. Из некоторого листового материала необходимо выкроить 360 заготовок типа А, 300 заготовок типа Б и 675 заготовок типа С. При этом можно применять три способа раскроя. Количество заготовок, получаемых из каждого листа при каждом способе раскроя, указано в следующей таблице:
|
Тип заготовки |
Способ раскроя | ||
|
1 |
2 |
3 | |
|
A |
3 |
2 |
1 |
|
B |
1 |
6 |
2 |
|
C |
4 |
1 |
5 |
Определить количество листового материала, подлежащего раскрою каждым из способов, чтобы выполнить плановое задание по всем заготовкам.
Решение.
Обозначим через
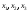 количество листов материала, раскраиваемых
соответственно первым, вторым и третьим
способами. Тогда при первом способе
раскроя
количество листов материала, раскраиваемых
соответственно первым, вторым и третьим
способами. Тогда при первом способе
раскроя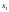 листов будет получено 3
листов будет получено 3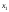 заготовок типа А, при втором – 2
заготовок типа А, при втором – 2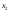 ,
при третьем – 1
,
при третьем – 1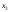 .
Для полного выполнения задания по
заготовкам типа А сумма 3
.
Для полного выполнения задания по
заготовкам типа А сумма 3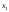 +2
+2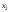 +1
+1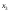 должна равняться 360, т.е.
должна равняться 360, т.е.
3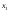 +2
+2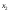 +1
+1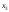 =360.
=360.
Аналогично получаем уравнения
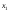 +6
+6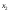 +2
+2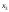 =300,
=300,
4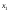 +
+ +5
+5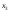 =675,
=675,
которым
должны удовлетворять неизвестные
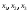 для того, чтобы выполнить задание по
заготовкам Б и С.
для того, чтобы выполнить задание по
заготовкам Б и С.
По
смыслу задачи
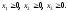
Таким образом, система:
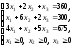
выражает в математической форме условия выполнения всего задания по заготовкам A,B,C, а задача сводится к нахождению опорных неотрицательных решений системы линейных уравнений
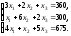
Применим алгоритм нахождения опорных решений, основанный на методе Жордана-Гаусса



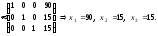
Ответ: 90 листов материала следует раскраивать первым способом,
15 листов – вторым способом и 15 – третьим способом.
Пример
5. Предприятие
состоит из трех цехов, каждый выпускает
один вид продукции. Расходные коэффициенты
(«прямые» затраты)
 – количество единиц продукцииi-го
цеха, используемое как «сырье» для
выпуска единицы продукции j-го
цеха, заданы матрицей А. Количество
единиц продукции i-го
цеха, предназначенных для реализации
(конечный продукт), задается матрицей
Y.
– количество единиц продукцииi-го
цеха, используемое как «сырье» для
выпуска единицы продукции j-го
цеха, заданы матрицей А. Количество
единиц продукции i-го
цеха, предназначенных для реализации
(конечный продукт), задается матрицей
Y.
Определить:
коэффициенты полных затрат;
валовой выпуск (план) для каждого цеха;
производственную программу цехов;
коэффициенты косвенных затрат.
 ;
;
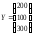 .
.
Решение.
Обозначим производственную программу
завода через
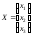 ,
где
,
где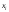 – валовой выпуск продукцииi-го
цеха, а план выпуска товарной продукции
– через
– валовой выпуск продукцииi-го
цеха, а план выпуска товарной продукции
– через
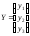 (он задан по условию).
(он задан по условию).
Тогда производственные взаимосвязи завода можно представить следующей системой трех уравнений
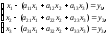
где
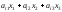 – внутрипроизводственное потреблениеi-го
цеха,
– внутрипроизводственное потреблениеi-го
цеха,
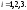
Запишем эту систему в матричной форме
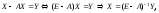
где
 .
.
Элементы обратной матрицы
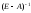 будут представлять собой искомые
коэффициенты полных внутрипроизводственных
затрат.
будут представлять собой искомые
коэффициенты полных внутрипроизводственных
затрат.
Выполнив расчеты, получим
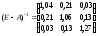 .
.
Таким образом, например, для выпуска единицы продукции первого, второго и третьего цехов необходимо затратить продукции соответственно 1,04; 0,21 и 0,03 единиц.
Для определения валового выпуска продукции цехов воспользуемся равенством
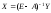 :
:

Следовательно,
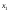 =238,
=238,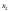 =187,
=187,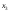 =400.
=400.
Производственную программу каждого из цехов определим из соотношения
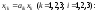
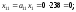
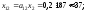

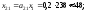
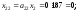
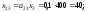
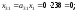
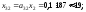
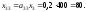
В результате получим следующую балансовую таблицу:
|
Цеха |
Внутрипроизводст. потребление |
Итого
|
Конечный
продукт
|
Валовой
выпуск
| ||
|
1 |
2 |
3 | ||||
|
1 |
0 |
37 |
0 |
37 |
200 |
238 |
|
2 |
48 |
0 |
40 |
88 |
100 |
187 |
|
3 |
0 |
19 |
80 |
99 |
300 |
400 |
Косвенные затраты найдем по формуле
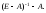
 .
.
Замечание. Все расчеты в задаче выполнены с точностью до 0,01.
Пример
6. Имеется
три страны
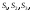 национальный доход каждой равен
соответственно
национальный доход каждой равен
соответственно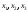 .
Известна структурная матрица
.
Известна структурная матрица

торговли этих
стран, где
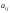 – доля национального дохода, которую
страна
– доля национального дохода, которую
страна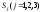 тратит на покупку товаров у страны
тратит на покупку товаров у страны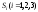 .
.
Будем считать, что
весь национальный доход тратится на
закупку товаров либо внутри страны,
либо на импорт из других стран, поэтому
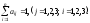
Требуется найти национальные доходы стран для сбалансированной торговли.
Решение.
Для любой страны
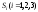 выручка от внутренней и внешней торговли
составит:
выручка от внутренней и внешней торговли
составит: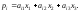
Для
сбалансированной торговли необходима
бездефицитность торговли каждой страны
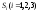 ,
т.е. выручка от торговли каждой страны
должна быть не меньше ее национального
дохода:
,
т.е. выручка от торговли каждой страны
должна быть не меньше ее национального
дохода: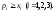
Если
считать, что
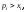 то
получим систему неравенств
то
получим систему неравенств
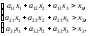
Сложив все неравенства этой системы, получим
 +
+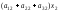 +
+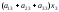 >
>
>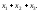
Учитывая, что в структурной матрице сумма элементов каждого столбца равна единице, получим противоречивое неравенство
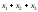 >
>
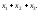
Таким
образом, неравенство
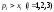 невозможно, и условие
невозможно, и условие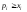 принимает вид
принимает вид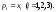 С экономической точки зрения это понятно,
так как все страны не могут одновременно
получать прибыль. Задача сводится к
решению системы уравнений:
С экономической точки зрения это понятно,
так как все страны не могут одновременно
получать прибыль. Задача сводится к
решению системы уравнений:
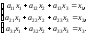
Запишем
систему в матричной форме
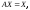 где
где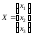 – матрица из национальных доходов
стран. Таким образом, эта же задача в
свою очередь сводится к отысканию
собственного вектора матрицы
– матрица из национальных доходов
стран. Таким образом, эта же задача в
свою очередь сводится к отысканию
собственного вектора матрицы ,
отвечающего собственному значению
,
отвечающего собственному значению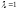 .
.
Используем
уравнение
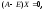 где
где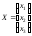 – нуль-матрица.
– нуль-матрица.
 .
.
Получаем систему уравнений:
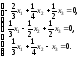
Решим систему, например, методом Гаусса.




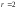 –число базисных
неизвестных;
–число базисных
неизвестных;
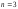 – число неизвестных системы уравнений;
– число неизвестных системы уравнений;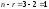 – число свободных неизвестных. Система
неопределенная.
– число свободных неизвестных. Система
неопределенная.
Из последней
матрицы
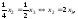 где
где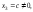
 – любое действительное число, т.е.
– любое действительное число, т.е.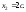
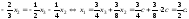
Таким
образом,
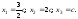
Полученный результат
означает, что сбалансированность
торговли трех стран достигается при
векторе национальных доходов
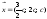 ,
т.е. при соотношении национальных доходов
стран
,
т.е. при соотношении национальных доходов
стран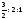 или 3 : 4 : 2.
или 3 : 4 : 2.
Пример 7. Привести квадратичную форму к каноническому виду методом Лагранжа и записать соответствующее преобразование
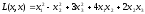 .
.
Решение.
Следуя алгоритму метода Лагранжа,
выделим вначале в квад-ратичной форме
все члены, содержащие
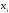 ,
и дополним их до полного квадрата:
,
и дополним их до полного квадрата:
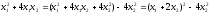 .
.
Сделаем
в этом выражении замену
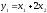 и подставим его в квадратичную форму.
Получим:
и подставим его в квадратичную форму.
Получим:
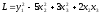 .
.
Далее
выделим в
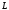 члены, содержащие
члены, содержащие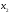 и проделаем с ними анало-гичную процедуру:
и проделаем с ними анало-гичную процедуру:
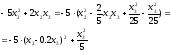
Если
положить
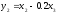 ,
то квадратичная форма уже не будет
содержать смешанных произведений.
Примем также
,
то квадратичная форма уже не будет
содержать смешанных произведений.
Примем также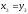 ,
тогда
,
тогда
109
канонический вид квадратичной формы есть
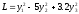 .
.
Соответствующее
преобразование от переменных
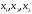 к переменным
к переменным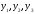 имеет вид:
имеет вид:
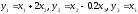 .
.
Пример 8. Найти ортогональное преобразование, приводящее квадратичную форму к каноническому виду, и записать соответствующий канонический вид этой формы:
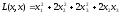 .
.
Решение.
В исходном базисе
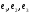 матрица оператора, соответствующая
данной квадратичной форме, есть
матрица оператора, соответствующая
данной квадратичной форме, есть
 .
.
Эта
матрица будет определять квадратичную
форму канонического вида в ортонормированном
базисе
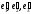 ,
составленном из собственных векторов
матрицы
,
составленном из собственных векторов
матрицы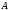 .
Найдем их.
.
Найдем их.
Характеристическое
уравнение для матрицы
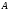 имеет вид
имеет вид
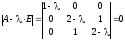 .
.
Откуда следует
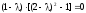 и
и
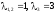 .
.
Как известно собственные векторы матрицы находятся из уравнений
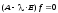 .
.
Для
случая
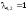 имеем:
имеем:

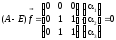 .
.
110
Ранг
матрицы этой системы уравнений
(относительно
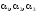 )
равен 1. Следовательно, ФСР системы
состоит из двух линейно независимых
решений.
)
равен 1. Следовательно, ФСР системы
состоит из двух линейно независимых
решений.
Как
видно из данной системы, величина
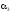 принимает произвольные значения, а
величины
принимает произвольные значения, а
величины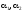 связаны соотношением
связаны соотношением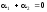 .В
качестве собственных можно выбрать,
например, векторы
.В
качестве собственных можно выбрать,
например, векторы
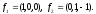
Эти
векторы ортогональны:
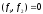 (если бы они оказались не ортогональными,
то их нужно было бы ортогонализировать
с помощью стандартной процедуры). Вектор
(если бы они оказались не ортогональными,
то их нужно было бы ортогонализировать
с помощью стандартной процедуры). Вектор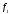 к тому же и нормирован. Откуда следует
-
к тому же и нормирован. Откуда следует
-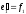 .
Нормируем теперь вектор
.
Нормируем теперь вектор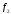 :
:
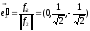 .
.
Для
случая
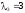 уравнение, определяющее собственный
вектор есть
уравнение, определяющее собственный
вектор есть

 .
.
Ранг
матрицы этой системы уравнений равен
2. Следовательно она имеет одно линейно
независимое решение, например,
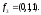 Отнормируем этот вектор:
Отнормируем этот вектор: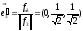 .
.
Теперь можно составить искомую матрицу ортогонального преобразования:
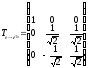 .
.
111
Исходная квадратичная форма будет иметь следующий канонический вид
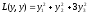 .
.
При
этом переменные
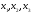 связаны с переменными
связаны с переменными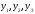 соотношением
соотношением
 или
или