Виды дифференциальных уравнений второго порядка

1. Уравнения, не содержащие искомой функции , - уравнения вида:

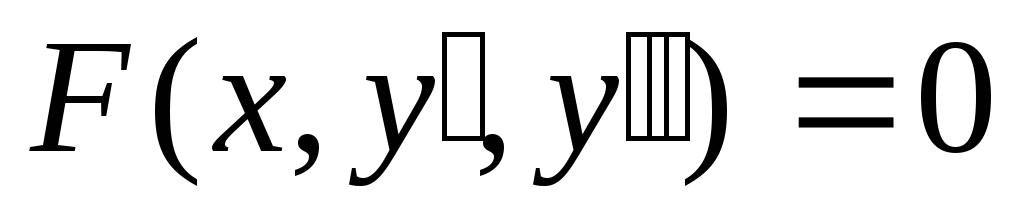
В этом случае надо ввести новую неизвестную функцию , положив, тогдаи функция перепишется в виде:, т.е. оказывается уравнением первого порядка относительно. Решив его по плану решения дифференциального уравнения первого порядка (см. выше), найдем, т.е., тогда.

Пример: Решить дифференциальное уравнение второго порядка

Введем новую переменную , тогда получим-дифференциальное уравнение первого порядка относительно переменной, решим его плану решения дифференциального уравнения первого порядка с разделяющимися переменными (см. выше)

Заменим через дифференциалы, т.е., получим

Помножим это равенство на , получим

Разделим переменные, т.е. разделим обе части данного равенства на , получим

Когда переменные отделены, проинтегрируем выражение, получим

По таблице интегралов находим интегралы функций, получим

Выразим , для этого применим свойство логарифмов: разность логарифмов равна логарифму частного, т.е., следовательно

, отсюда по определению логарифма имеем, или

Теперь заменим на, получим, опять получили дифференциальное уравнение первого порядка относительно функции, решаем его аналогично

Т.о. решением дифференциального уравнения будет функция , где- некоторые постоянные (константы).

2. Уравнения, не содержащие независимой переменной , - уравнения вида:

В этом случае надо за новую неизвестную функцию принять, положив, а за новую независимую переменную принять, тогдаи функция перепишется в виде:, т.е. оказывается уравнением первого порядка относительно. Решив его по плану решения дифференциального уравнения первого порядка (см. выше), найдем, т.е., тогда.

Пример: Решить дифференциальное уравнение

Введем новую переменную , положиви, получим

Помножим уравнение на и разделим на, получим

Разделим переменные, поделив выражение на произведение , получим

Проинтегрируем уравнение, получим

Найдем интегралы функций по таблице, получим

Выразим из уравнения , для этого применим свойства логарифмов:, и, а также определение логарифма, получим

Заменим , получим

Помножим равенство на и разделим на, получим

Проинтегрируем равенство, получим

Найдем интегралы по таблице и выразим , получим

Т.о. решением дифференциального уравнения будет функция.

Задания для решения.

1. Решить дифференциальное уравнение первого порядка:

1. ; 2.; 3.; 4.; 5.;

6. ; 7.; 8.; 9.; 10.;

11. ; 12.; 13.; 14.;

15. ; 16.; 17.; 18.;

19. ; 20.; 21.; 22.;

23. ; 24.; 25..

2. Решить дифференциальное уравнение второго порядка:

1. ; 2.; 3.; 4.;

5. ; 6.; 7.; 8.;

9. ; 10.; 11.; 12..

Дополнительные задания.

1. Решить дифференциальное уравнение первого порядка:

1. ; 2.; 3.; 4.; 5.;

6. ; 7.; 8.; 9.;

10. ; 11.; 12.; 13.

14. ; 15.; 16.;

17. ; 18.; 19.;

20. ; 21.; 22.;

23. ; 24.; 25..

2. Решить дифференциальное уравнение второго порядка:

1. ; 2.; 3.; 4.;

5. ; 6.; 7.; 8.;

9. ; 10.; 11.; 12..

Варианты заданий

Выбор варианта осуществляется в соответствии с порядковым номером в списке журнала. Первая цифра относится к первому заданию, а вторая – ко второму.

	0.	1.	2.	3.	4.	5.	6.	7.	8.	9.
0.		1,11	13,12	9,10	6,5	4,8	18,7	23,7	12,7	14,11
1.	12,4	13,8	1,11	5,7	17,8	8,2	19,10	21,9	12,3	3,2
2.	4,7	15,12	6,7	7,3	8,10	9,2	20,3	22,11	13,9	14,4
3.	5,6	6,4	7,9	8,5	9,7	11,12	2,12	3,11	4,6	5,3
4.	16,5	10,2	24,5	20,1	6,10	9,8	7,7	25,10	8,4	21,10