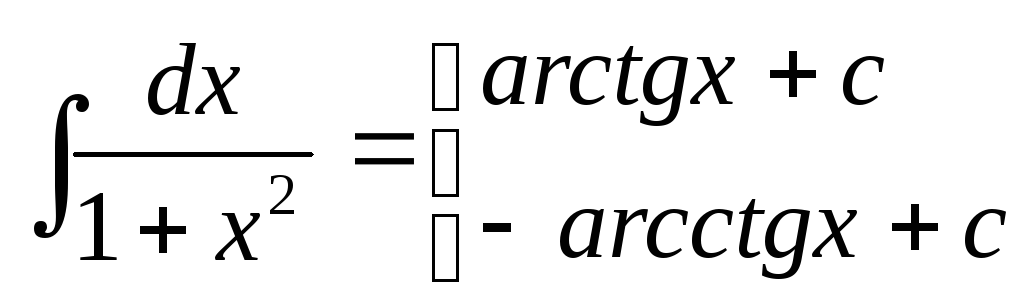- •Инструкционная карта № 1.
- •Тема: Решение задач. Выполнение операций над множествами.
- •Задания для решения.
- •Дополнительные задания.
- •Теорема №1: Если функция имеет производную в точке, а функцияимеет производную в соответствующей точке, то сложная функцияимеет производную в точке. В этом случае имеет место следующая формула:
- •Задания для решения.
- •1. ; 2.; 3.;
- •4. ; 5.;
- •6. ; 7.;
- •8. ; 9.; 10..
- •Контрольные вопросы
- •Инструкционная карта № 5.
- •Тема: Решение дифференциальных уравнений.
- •Виды дифференциальных уравнений второго порядка
- •Задания для решения.
- •Контрольные вопросы
- •Инструкционная карта № 6.
- •Тема: Решение задач на определение вероятностей событий.
- •Задания для решения.
- •Дополнительные задания.
- •Варианты заданий Выбор варианта осуществляется в соответствии с порядковым номером в списке журнала. Выполняются два примера задания.
- •Контрольные вопросы
1. ; 2.; 3.;
4. ; 5.;
6. ; 7.;
8. ; 9.; 10..
Таблица неопределенных интегралов.
|
1.
|
8.
|
15.
|
|
2.
|
9.
|
16.
|
|
3.
|
10.
|
17.
|
|
4.
|
11.
|
18.
|
|
5.
|
12.
|
19.
|
|
6.
|
13.
|
20.
|
|
7.
|
14.
|
21.
|
Пример:
1. Найти интеграл:

Здесь применили свойства № 4 и №5 (т.е. интеграл от алгебраической суммы нескольких функций равен алгебраической сумме интегралов; и постоянный множитель можно вынести из под знака интеграла), а также формулы таблицы № 10, № 2, № 4, №5 и №13.
Вычислить интеграл:

Здесь применили свойства № 6 и № 7 (т.е. интеграл от алгебраической суммы нескольких функций равен алгебраической сумме интегралов; и постоянный множитель можно вынести из под знака интеграла), формулы таблицы № 4 и № 3, а также определение определённого интеграла.
Задания для решения.
1. Найти неопределенный интеграл:
1.
![]() ;
2.
;
2.![]() ;
3.
;
3.![]() ;
4.
;
4.![]() ;
5.
;
5.![]() ;
6.
;
6.![]() ;
;
7.
![]() ;
8.
;
8.![]() ;
9.
;
9.![]() ;
;
10.
![]() ;
11.
;
11.![]() ;
12.
;
12.![]() ;
13.
;
13.![]() ;
;
14.
![]() ;
15.
;
15.![]() ;
16.
;
16.![]() ;
17.
;
17.![]() ;
;
18.
![]() ;
19.
;
19.![]() ;
20.
;
20.![]() ;
21.
;
21.![]() ;
;
22.
![]() ;
23.
;
23.![]() ;
24.
;
24.![]() .
.
2. Вычислить определённый интеграл:
1.
![]() ;
2.
;
2.![]() ;
3.
;
3.![]() ;
4.
;
4.![]() ;
5.
;
5. ;
6.
;
6.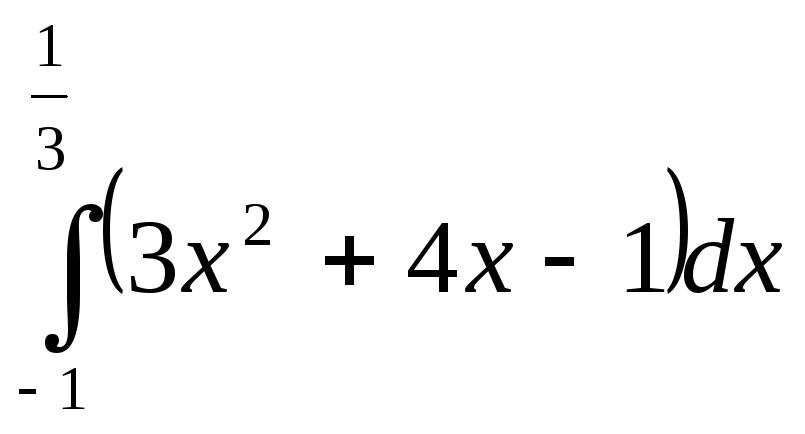 ;
;
7.
![]() ;
8.
;
8.![]() ;
9.
;
9.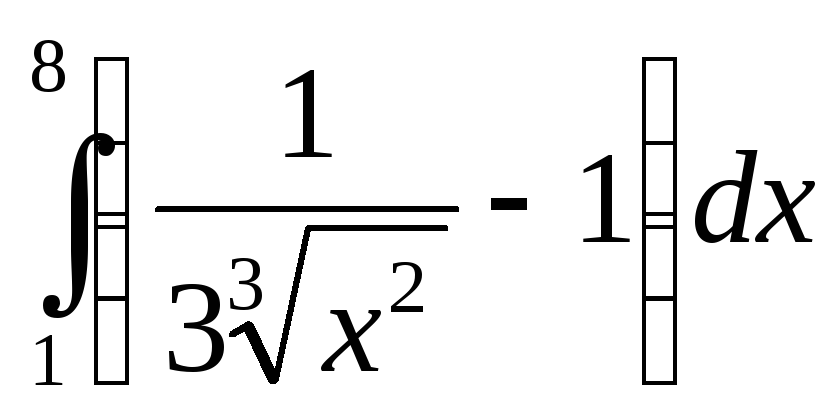 ;
10.
;
10.![]() ;
;
11.
![]() ;
12.
;
12. ;
13.
;
13. ;
14.
;
14.![]() ;
;
15.
![]() ;
16.
;
16.![]() ;
17.
;
17.![]() ;
18.
;
18.![]() ;
19.
;
19.![]() .
.
Дополнительные задания.
Рассчитать неопределённый интеграл:
1.
![]() ;
2.
;
2.![]() ;
3.
;
3.![]() ;
4.
;
4.![]() ;
5.
;
5.![]() ;
6.
;
6.![]() ;
;
7.
![]() ;
8.
;
8.![]() ;9.
;9.
![]() ;
;
10.
![]() ;
11.
;
11.![]() ;
12.
;
12.![]() ;
13.
;
13.![]() ;
;
14.
![]() ;
15.
;
15.![]() ;
16.
;
16.![]() ;
17.
;
17.![]() ;
;
18.
![]() ;19.
;19.
![]() ;
20.
;
20.
![]() .
.
Вычислить определённый интеграл:
1.
![]() ;
2.
;
2.![]() ;
3.
;
3. ;
4.
;
4. ;
5.
;
5. ;
6.
;
6.![]() ;
;
7.
![]() ;
8.
;
8.![]() ;9.
;9.
 ;
10.
;
10.
![]() ;
;
11.
 ;
12.
;
12. ;
13.
;
13.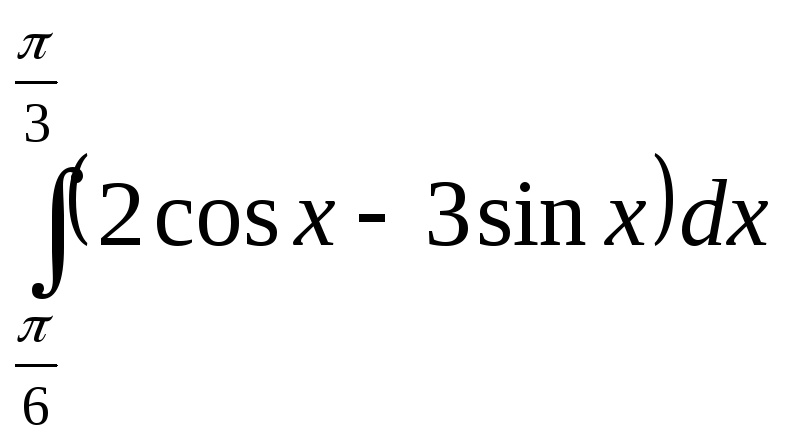 ;
14.
;
14.![]() ;
;
15.
![]() ;
16.
;
16.![]() ;
17.
;
17.![]() ;
18.
;
18.![]() ;19.
;19.
![]() .
.
Варианты заданий
Выбор варианта осуществляется в соответствии с порядковым номером в списке журнала. Первая цифра относится к первому заданию, а вторая – ко второму.
|
|
0. |
1. |
2. |
3. |
4. |
5. |
6. |
7. |
8. |
9. |
|
0. |
|
1,17 |
13,16 |
9,19 |
6,15 |
4,18 |
18,7 |
3,7 |
12,7 |
14,11 |
|
1. |
12,4 |
13,8 |
1,4 |
5,7 |
17,8 |
8,2 |
19,3 |
1,13 |
12,3 |
3,2 |
|
2. |
4,7 |
15,12 |
6,17 |
7,3 |
8,10 |
9,2 |
20,13 |
2,15 |
13,9 |
14,4 |
|
3. |
5,6 |
6,14 |
7,9 |
8,5 |
9,7 |
11,12 |
2,6 |
3,11 |
4,6 |
5,3 |
|
4. |
16,5 |
10,2 |
4,5 |
20,1 |
6,10 |
9,5 |
7,7 |
5,10 |
8,4 |
10,10 |
Контрольные вопросы
Сформулируйте определение первообразной, неопределенного интеграла, определенного интеграла.
Назовите свойства интегралов.
Инструкционная карта № 5.
Практическое занятие № 5 по теме «Дифференциальные уравнения».
Тема: Решение дифференциальных уравнений.
Краткая теория темы.
Опр. Уравнения, в которых неизвестными являются функции и в которые входят не только сами функции, но и их производные, называется дифференциальными уравнениями.
Опр.
Если в
уравнение входит независимая переменная,
неизвестная функция и её первая
производная, то это уравнение называется
дифференциальным уравнением первого
порядка. В общем виде оно записывается
так:
![]() (1), где
(1), где![]() - искомая неизвестная функция,
- искомая неизвестная функция,![]() - её производная по х, а
- её производная по х, а![]() -
заданная функция переменных
-
заданная функция переменных![]() .
.
Опр.
Решением
дифференциального уравнения (1) называется
такая функция
![]() ,
которая будучи подставлена в
дифференциальное уравнение вместо
,
которая будучи подставлена в
дифференциальное уравнение вместо![]() (при этом вместо
(при этом вместо![]() подставляется
подставляется![]() )
обращает уравнение (1) в тождество.
)
обращает уравнение (1) в тождество.
Опр.
Общим решением
дифференциального уравнения (1) называется
такая функция
![]() ,
которая при каждом фиксированном
значении
,
которая при каждом фиксированном
значении![]() как функция от
как функция от![]() является решением уравнения (1).
является решением уравнения (1).
Опр.
Дифференциальные уравнения вида
![]() ,
где
,
где![]() и
и![]() - заданные функции, называется уравнением
первого порядка с отделенными переменными.
- заданные функции, называется уравнением
первого порядка с отделенными переменными.
План решения дифференциальных уравнений первого порядка с отделенными переменными.
Заменяем производную
 через дифференциалы, т.е.
через дифференциалы, т.е. ,
получим
,
получим ;
;Умножаем обе части уравнения на
 ,
получим
,
получим ,
здесь первое слагаемое
,
здесь первое слагаемое зависит только от
зависит только от ,
а второе
,
а второе - только от
- только от ,
следовательно переменные отделены;
,
следовательно переменные отделены;Когда переменные отделены, интегрируем уравнение, т.е.
 ,
находим интегралы по таблице, получим
,
находим интегралы по таблице, получим ;
;Решаем последнее уравнение относительно
 ,
получим общее решение:
,
получим общее решение: .
.
Пример:
1. Решить уравнение:
![]()
1)
![]() ,
,![]() ;
;
2)
![]() ;
;
3)
![]() ,
,![]() ;
;
4)
![]() - общее решение уравнения.
- общее решение уравнения.
2.
Решить уравнение:
![]()
1)
![]() ,
,![]() ;
;
2)
![]() ;
;
3)
![]() ,
,![]() ;
;
4)
![]() ,
по определению логарифма
,
по определению логарифма![]() -
общее решение уравнения.
-
общее решение уравнения.
Опр.
Дифференциальные
уравнения вида
![]() ,
где
,
где![]() - заданные функции, называется
дифференциальным уравнением первого
порядка с разделяющимися переменными.
- заданные функции, называется
дифференциальным уравнением первого
порядка с разделяющимися переменными.
План решения дифференциальных уравнений первого порядка с разделяющимися переменными.
Заменяем производную
 через дифференциалы, т.е.
через дифференциалы, т.е. ,
получим
,
получим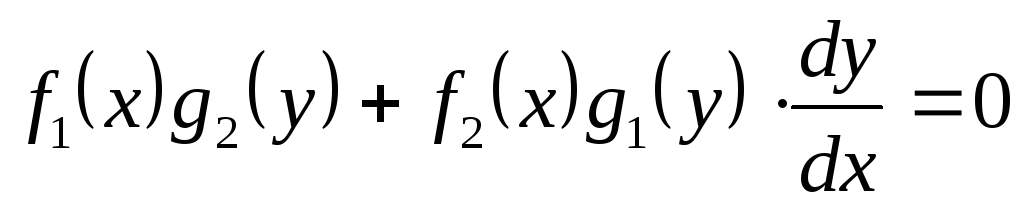 ;
;Умножаем обе части уравнения на
 ,
получим
,
получим ,
в первом слагаемом кроме множителей,
содержащих переменную
,
в первом слагаемом кроме множителей,
содержащих переменную ,
имеются множители с переменной
,
имеются множители с переменной ,
а во втором – кроме множителей, содержащих
переменную
,
а во втором – кроме множителей, содержащих
переменную ,
имеются множители с переменной
,
имеются множители с переменной ,
нам нужно избавиться от этих «мешающих»
множителей. Поэтому поделим обе части
данного уравнения на произведение этих
множителей, т.е. поделим на
,
нам нужно избавиться от этих «мешающих»
множителей. Поэтому поделим обе части
данного уравнения на произведение этих
множителей, т.е. поделим на ,
получим:
,
получим: -
получили уравнение с отделенными
переменными;
-
получили уравнение с отделенными
переменными;Когда переменные отделены, интегрируем уравнение, т.е.
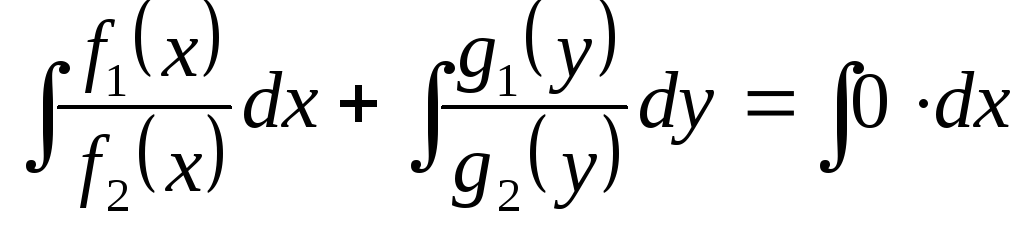 ,
находим интегралы по таблице, получим
,
находим интегралы по таблице, получим ;
;Решаем последнее уравнение относительно
 ,
получим общее решение:
,
получим общее решение: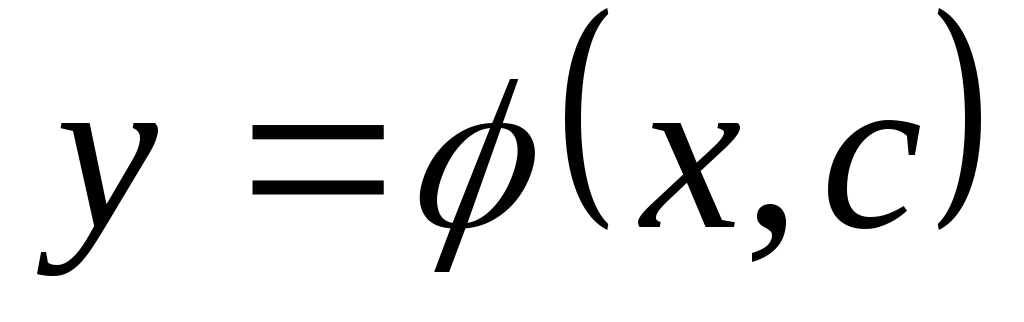 .
.
Пример: Решить уравнение:![]()
1)
![]() ,
,![]() ;
;
2)
![]() ,
разделим на
,
разделим на![]() ,
получим
,
получим![]() ;
;
3)
![]() ,
,![]() ,
применим свойство логарифмов: сумма
логарифмов равна логарифму произведения,
получим
,
применим свойство логарифмов: сумма
логарифмов равна логарифму произведения,
получим![]() ;
;
4)
![]() ,
по определению логарифма
,
по определению логарифма
![]() ,
- общее решение уравнения.
,
- общее решение уравнения.
Опр.
Если в
уравнение входит независимая переменная,
неизвестная функция, её первая и вторая
производные, то это уравнение называется
дифференциальным уравнением второго
порядка. В общем виде оно записывается
так:
![]() (2), где
(2), где![]() - искомая неизвестная функция,
- искомая неизвестная функция,![]() - её первая производная по х,
- её первая производная по х,![]() - её вторая производная, а
- её вторая производная, а![]() -
заданная функция переменных
-
заданная функция переменных![]() .
.
Опр. Решением дифференциального
уравнения (2) называется такая функция![]() ,
которая будучи подставлена в
дифференциальное уравнение вместо
,
которая будучи подставлена в
дифференциальное уравнение вместо![]() (при
этом вместо
(при
этом вместо![]() подставляются соответственно
подставляются соответственно![]() )
обращает уравнение (2) в тождество.
)
обращает уравнение (2) в тождество.