
Degtyarenko_dlya_studentov_II_kursa_2013 / Детерминир. модели / Лекции Дет. модели. Часть 2
.pdfзрения. Предполагая, что k1 k2 k1 0,k2 0 , рассмотрите следующие случаи.
|
|
|
|
|
|
k1 |
|
|
1. |
Схема |
обратимой |
реакции такова: |
|
B. |
Здесь |
||
A |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k2 |
|
A и B |
|
CA0 0,CB0 0 – это начальные концентрации реагентов |
|||||||
|
соответственно, причем CA0 CB0. |
|
k1 |
|
|
|||
|
|
|
|
|
|
|
|
|
2. |
Схема |
обратимой |
реакции |
такова: |
A B |
|
|
Здесь |
C D. |
||||||||
|
|
|
|
|
|
|
|
|
|
CA0,CB0,CC0,CD0 |
|
|
|
k2 |
|
|
|
|
– это |
начальные |
концентрации |
реагентов |
||||
|
A,B,C,D соответственно, причем все они отличны от нуля и по- |
|||||||
парно различны между собой.
2. Математическая модель. Для составления математических моделей задач данного раздела необходимо знание общих сведений из химической кинетики, кратко изложенных в подразделе 1.3.
1. В обратимых реакциях превращение реагента в продукт осложняется одновременным обратным превращением. В соответствии с принципом независимости протекания элементарных стадий скорость обрати-
мой реакции определяется разностью скоростей прямой и обратной
|
k1 |
стадий. Математической моделью, соответствующей схеме A |
|
B |
k2
обратимой реакции, является система обыкновенных дифференциальных уравнений
dCA(t) |
k C |
A |
(t) k |
C |
B |
(t), |
dCB(t) |
k C |
A |
(t) k |
C |
B |
(t), |
|
|
||||||||||||
dt |
1 |
2 |
|
|
dt |
1 |
2 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
дополненная системой начальных условий из пункта 1. Эта система включает в себя две неизвестные функции, причем, нетрудно заметить, что функции CA t и CB t , рассматриваемые при t 0, отличаются друг от друга на постоянную величину. При математическом моделировании химического процесса, описываемого предложенной в задании кинетической схемой, можно обойтись введением лишь одной неизвестной функции, через которую (и константы) выражаются обе искомые функции. С этой целью удобно использовать, например, функцию x(t) – количество (моль) вещества B, находящееся в единице реакционного объема к моменту времени t 0, за вычетом начальной концентрации
68
этого вещества. В соответствии со стехиометрией реакционной схемы прямая и обратная стадии имеют первый кинетический порядок, и текущие концентрации реагентов в рассматриваемый момент времени t 0 выражаются так: CA t CA0 x(t), CB t CB0 x(t). Тогда каждое дифференциальное уравнение из математической модели реакции, на-
пример, |
|
|
dCA(t) |
k C |
A |
(t) k |
2 |
C |
B |
(t), можно переписать в виде |
|||||||
|
|
|
|||||||||||||||
|
|
|
|
|
|
dt |
1 |
|
|
|
|
|
|
||||
|
dx(t) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
k |
C |
A0 |
x(t) k |
2 |
C |
B0 |
x(t) . Ему соответствует начальное усло- |
|||||||||
|
|
||||||||||||||||
|
dt |
1 |
|
|
|
|
|
|
|
|
|
|
|
||||
вие x 0 0. Итак, математическая модель для случая 1 такова: |
|||||||||||||||||
|
|
|
|
|
|
|
|
CA t CA |
x(t) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
(t 0), |
|
|
|
|
|
|
|
|
|
CB t CB0 x(t) |
|||||||||
где CA0 CB0 – это заданные в условии ненулевые начальные концен-
трации |
|
реагентов, |
а |
|
x(t) |
– |
это |
|
решение |
задачи |
Коши |
|||||||||
|
dx(t) |
k |
C |
A0 |
x(t) k |
2 |
C |
B0 |
x(t) , |
x 0 0, |
которую |
можно |
перепи- |
|||||||
|
|
|||||||||||||||||||
|
dt |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
x |
|
|
du |
|
|
|
|
|
t |
|
|
сать в интегральной форме: |
|
|
|
|
|
|
|
dt. |
|
|||||||||||
k C |
A0 |
u k |
2 |
C |
B0 |
u |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
0 1 |
|
|
|
|
0 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k1 |
|
|
||
|
2. Двусторонняя реакция, схема которой |
|
|
|
C D, относит- |
|||||||||||||||
|
A B |
|
||||||||||||||||||
k2
ся к обратимым реакциям второго порядка. В реакции такого типа, по крайней мере, одна из стадий должна иметь второй кинетический порядок. Вообще говоря, возможны восемь различных кинетических схем для двусторонних реакций второго порядка.
Упражнение. Запишите все эти схемы.
k1
Математической моделью, соответствующей схеме A B |
C D |
k2
обратимой реакции, является система обыкновенных дифференциальных уравнений
dCA(t) |
|
k C |
(t)C |
B |
(t) k |
C |
C |
(t)C |
D |
(t), |
dCB(t) |
|
dCA(t) |
, |
|
|
|||||||||
|
|
|
|
|
|
|
|||||||||||||||||||
dt |
1 |
|
A |
|
|
|
2 |
|
|
|
|
|
dt |
|
|
|
dt |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
dCC(t) |
k C |
A |
(t)C |
B |
(t) k |
C (t)C |
D |
(t) |
dCA(t) |
, |
dCD(t) |
|
dCA(t) |
, |
|||||||||||
|
|
|
|
||||||||||||||||||||||
dt |
1 |
|
|
|
2 |
|
C |
|
|
|
|
|
dt |
|
|
|
dt |
dt |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
69 |
|
|
|
|
|
|
|
|
|
|
|
|
дополненная системой начальных условий из пункта 2. Эта система включает в себя четыре неизвестные функции, причем, нетрудно заметить, что функции CA t и CB t , CA t и CC t , CA t и CD t , рассматриваемые при t 0, отличаются друг от друга на соответствующую постоянную величину. При математическом моделировании химического процесса, описываемого предложенной в задании кинетической схемой, можно обойтись введением лишь одной неизвестной функции, через которую (и константы) выражаются все искомые функции. С этой целью удобно использовать, например, функцию x(t) – количество (моль) вещества C, находящееся в единице реакционного объема к моменту времени t 0, за вычетом начальной концентрации этого вещества. В соответствии со стехиометрией реакционной схемы прямая и обратная стадии имеют второй кинетический порядок и текущие концентрации реагентов в рассматриваемый момент времени t 0 выражаются следующим образом:
CA t CA0 x(t),CB t CB0 x(t), CC t CC0 x(t), CD t CD0 x(t).
Тогда каждое дифференциальное уравнение из математической модели
реакции, например, |
dCA(t) |
k C |
A |
(t)C |
B |
(t) k |
2 |
C |
C |
(t)C |
D |
(t), можно пере- |
|||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
dt |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
dx(t) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
x(t) C |
|
x(t) . |
||||||
писать |
так: |
k C |
A0 |
x(t) C |
B0 |
x(t) k |
2 |
|
D0 |
||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||
|
|
|
dt |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C0 |
|
|
|
|||||||||||||
Ему соответствует |
начальное условие |
|
x 0 0. |
|
Итак, математическая |
||||||||||||||||||||||||||||||
модель для случая 2 такова: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
CA t CA0 x(t),CB t CB0 x(t), |
|
(t 0), |
|
|
|||||||||||||||||||||||||||||
|
|
C |
|
t C |
|
|
x(t),C |
D |
t C |
D0 |
x(t), |
|
|
||||||||||||||||||||||
|
|
|
C |
C0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
где CA0,CB0,CC0,CD0 – это начальные ненулевые концентрации реаген- |
|||||||||||||||||||||||||||||||||||
тов A,B,C,D соответственно, а x(t) |
– это решение задачи Коши |
|
|||||||||||||||||||||||||||||||||
|
dx(t) |
k C |
A0 |
x(t) C |
B0 |
x(t) k |
2 |
C |
|
|
x(t) C |
D0 |
x(t) , x 0 0, |
||||||||||||||||||||||
|
dt |
|
|
||||||||||||||||||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
C0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
которую можно переписать в интегральной форме:
x |
|
|
|
|
|
du |
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
dt. |
|
k |
C |
A0 |
u C |
B0 |
u k |
2 |
C |
C0 |
u C |
D0 |
u |
|
||
0 |
1 |
|
|
|
|
|
|
|
0 |
3. Решение математической модели средствами компью-
терной системы Mathematica. Прежде всего, приведем ряд встроенных функций компьютерной системы Mathematica, которые могут быть использованы при решении задач данного раздела.
70
Обозначение встроенной функции |
Действия |
|
D[expr,{var,n}] |
Вычисляет n-ную производную выражения |
expr, |
|
содержащего переменную var, по переменной var. |
|
|
В случае n=1 вместо {var,n} пишут var. Команду |
|
|
можно использовать для дифференцирования как |
|
|
заданных аналитически, так и интерполяционных |
|
|
функций. |
|
DSolve[eqns,funs,var] |
Стремится найти в явном аналитическом виде общее |
|
(DSolve[eqn,fun,var]) |
решение системы дифференциальных уравнений |
|
|
eqns (дифференциального уравнения eqn) относи- |
|
|
тельно искомых функций funs (искомой функции |
|
|
fun), зависящих (зависящей) от переменной var. |
|
|
Если в список уравнений eqns включить необходи- |
|
|
мое количество начальных или граничных условий, |
|
|
то данная встроенная функция стремится найти в |
|
|
явном аналитическом виде частное решение систе- |
|
|
мы дифференциальных уравнений (дифференциаль- |
|
|
ного уравнения). Эта функция может выдавать ре- |
|
|
шения уравнения или системы через специальные |
|
|
функции. В случае отсутствия у системы Mathe- |
|
|
matica ответа в аналитическом виде введенные дан- |
|
|
ные просто перепечатываются. |
|
Integrate[f[x],x] |
Вычисляет неопределенный интеграл от функции |
|
|
f[x] по переменной x. Произвольную константу, |
|
|
которая возникает при интегрировании, полагают |
|
|
равной нулю. Система Mathematica вычисляет |
|
|
большинство интегралов, которые выражаются че- |
|
|
рез стандартные математические функции, а также |
|
|
позволяет интегрировать выражения, содержащие |
|
|
специальные функции. Если система не может пред- |
|
|
ставить результат интегрирования в виде формулы, |
|
|
то она выдает введенное выражение без изменений. |
|
N[x,n] |
Преобразует точный результат x в приближенный c |
|
|
заданной точностью n значащих цифр. |
|
NDSolve[{eq1,eq2,…, |
Находит численное решение системы уравнений |
|
initialdata},{fun1, |
eq1,eq2,…,initialdata |
(eqn, |
fun2,…},{var,varmin, |
initialdata) относительно искомых функций |
|
varmax}] |
fun1, fun2, … (искомой функции fun), |
завися- |
(NDSolve[{eqn, |
щих (зависящей) от переменной var, которая изме- |
|
initialdata},fun, |
няется в пределах отрезка [varmin,varmax]. Реше- |
|
{var,varmin,varmax}]) |
ния находятся системой Mathematica в виде интер- |
|
|
поляционных функций. Интерполяционная функция |
|
|
– это объект вида |
|
|
InterpolatingFunсtion[{{varmin, |
|
|
varmax}},<Таблица данных>], |
|
|
71 |
|
|
который представляет собой таблицу значений |
|||||
|
функции |
fun(var) в различных точках |
vari из |
|||
|
отрезка |
[varmin,varmax] и позволяет найти зна- |
||||
|
чение функции в любой точке этого отрезка путем |
|||||
|
интерполяции табличных данных. При этом предпо- |
|||||
|
лагают, что в промежутках между заданными точ- |
|||||
|
ками функция является достаточно гладкой. Обычно |
|||||
|
при выводе результата вычислений указывается |
|||||
|
только диапазон определения |
интерполяционной |
||||
|
функции, а таблица данных изображается в виде |
|||||
|
символа |
«<>», т. е. результат имеет вид |
||||
|
InterpolatingFunction[{{varmin,varmax}}, |
|||||
|
< >]. С интерполяционной функцией можно обра- |
|||||
|
щаться так же, как и с любой другой встроенной |
|||||
|
функцией, т. е. дифференцировать, интегрировать, |
|||||
|
строить ее график. |
|
|
|
||
NIntegrate[f[x], |
В случае, когда определенный интеграл не содержит |
|||||
{x,xmin,xmax}] |
неизвестных числовых параметров, дает численный |
|||||
|
результат интегрирования функции f[x] по пере- |
|||||
|
менной x в пределах интегрирования от xmin до |
|||||
|
xmax. |
|
|
|
|
|
ParametricPlot[{x[t], |
Строит двумерный график функции, заданной пара- |
|||||
y[t]},{t,tmin,tmax}, |
метрически, где значения параметра t принадлежат |
|||||
option->value] |
отрезку[tmin,tmax]. Эта встроенная функция имеет |
|||||
|
тот же набор опций, что и функция Plot, и позво- |
|||||
|
ляет строить график как одной, так и нескольких |
|||||
|
функций. При построении графиков нескольких |
|||||
|
функций в качестве первого аргумента в команде |
|||||
|
ParametricPlot |
необходимо указать |
список |
|||
|
функций, заданных параметрически. |
|
||||
Piecewise[{{val1, |
Задает кусочную функцию, определяемую как vali |
|||||
cond1},{val2,cond2},…}] |
на промежутке, указанном с помощью соответ- |
|||||
|
ствующего условия |
condi. |
|
|
||
Plot[{f1[x],f2[x],…, |
Строит |
на |
одном |
рисунке |
графики |
функций |
fn[x]},{xmin,xmax}] |
f1[x],f2[x],…,fn[x] одной переменной x на |
|||||
|
отрезке [xmin,xmax]. Существуют команды (формат |
|||||
|
их различен в различных версиях), например, |
|||||
|
Needs["PlotLegends`"] ‒ в версии Mathematica |
|||||
|
7.0, <<Graphics`Legend` ‒ в версии Mathematica |
|||||
|
5.2, которые подключают средства системы |
|||||
|
Mathematica, |
дающие возможность подписать гра- |
||||
|
фики на полученном рисунке. |
|
|
|||
ReplaceAll |
Оператор подстановки, который применяет список |
|||||
(expr/.rules) |
правил замены rules к выражению expr. |
|||||
|
|
|
|
|
|
|
|
|
72 |
|
|
|
|

Reduce[{ineq1,ineq2, |
Функция удобна для решения неравенств или сис- |
|
…},vars,dom] |
тем неравенств, рассматриваемых на области оп- |
|
|
ределения dom (dom может, например, принимать |
|
|
значения Integers, Reals, Complexes); в пре- |
|
|
делах рассматриваемой области определения dom |
|
|
дает результат решения системы неравенств |
|
|
{ineq1,ineq2, …} |
относительно переменных |
|
vars в виде набора простых неравенств. |
|
Simplify[expr] |
Находит для выражения |
expr простейшую форму, |
|
применяя к нему стандартные алгебраические пре- |
|
FullSimplify[expr] |
образования. |
expr простейшую форму, |
Находит для выражения |
||
|
применяя к нему более широкий спектр преобразо- |
|
|
ваний. |
|
Solve[eqns,vars] |
Делает попытку решить в символьной форме систе- |
|
|
му уравнений eqns относительно переменных |
|
|
vars (более подробное описание действия команды |
|
|
можно посмотреть в предыдущих разделах). |
|
Приведем фрагменты программного кода, снабженные пояснениями и комментариями.
1. Продемонстрируем различные варианты решения для первого случая. Например, можно получить аналитическое решение задачи Коши из математической модели обратимой реакции первого порядка при помощи метода разделения переменных с последующим интегрированием.
73
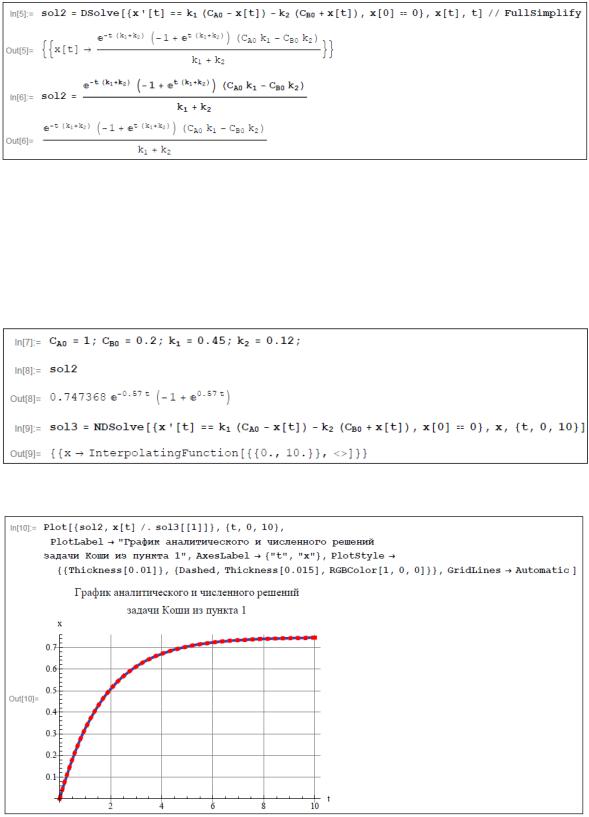
Можно получить аналитическое решение той же самой задачи Коши, применяя встроенную функцию DSolve.
Результаты, обозначенные sol1 и sol2, соответствующие указанным способам решения, идентичны. Можно при помощи встроенной функции NDSolve найти численное решение рассматриваемой задачи Коши в виде интерполяционной функции. Предположим, что t 0;10 , а константы скоростей прямой и обратной стадий и начальные концентрации реагирующих веществ принимают определенные числовые значения, указанные ниже.
Сравнивая графики численного решения и решения, полученного аналитическим путем, видим, что они идентичны.
74
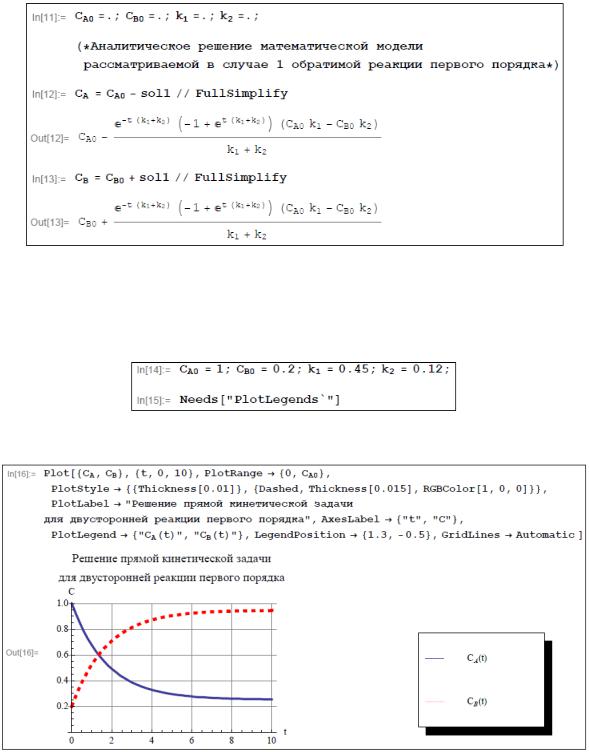
Вернемся к аналитическому решению рассматриваемой задачи Коши и запишем в общем виде аналитическое решение математической модели обратимой реакции первого порядка.
С целью построения графиков кинетических кривых зададим определенные числовые значения констант скоростей прямой и обратной стадий и начальных концентраций реагирующих веществ. Подключим средства системы Mathematica, дающие возможность подписать графики на полученном рисунке.
Представим графически полученные результаты. Приведем графики кинетических кривых для всех участников реакции.
Приведем также графики скоростей прямой и обратной стадий при тех же числовых значениях констант.
75
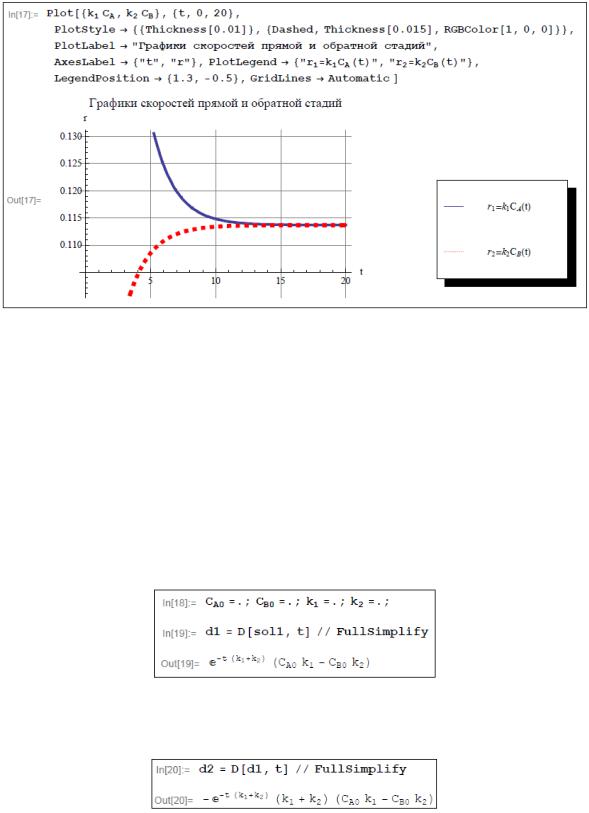
Решение математической модели, соответствующей случаю 1, закончено. В дальнейшем мы будем анализировать полученные результаты, поэтому приведем еще ряд математических выкладок, на которые будем ссылаться при формулировке выводов. Проведем исследование функции
x t |
e t k1 k2 |
1 et k1 k2 |
C |
A0 |
k C |
B0 |
k |
2 |
|
|
|
|
|
1 |
|
|
(она обозначена sol1). |
||||
|
k1 k2 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||
Прежде всего, отметим, что из математической модели следует выполне-
ние |
условия |
x t 0 при |
t 0. Поэтому |
можно утверждать, что |
|||||||
C |
A0 |
k C |
B0 |
k |
2 |
0. Заметим, |
что limx(t) |
CA0k1 |
CB0k2 |
. Проведем ис- |
|
|
|
||||||||||
|
1 |
|
|
t |
k1 |
k2 |
|||||
|
|
|
|
|
|
|
|||||
следование функции x t при помощи ее первой производной.
Первая производная положительна при t 0. Следовательно, функция x t возрастает на рассматриваемом промежутке. Проведем исследование функции x t при помощи ее второй производной.
Вторая производная отрицательна при t 0. Следовательно, график функции x t – выпуклый на рассматриваемом промежутке.
76

Из математической модели следует, что CA t CA0 x(t),
CB t CB0 x(t) при t 0. Следовательно, график функции CA t – мо-
нотонно убывающий и вогнутый, а график функции CB t – монотонно
возрастающий |
и |
выпуклый |
при |
t 0. |
Учитывая, |
что |
|
limx(t) |
CA0k1 |
CB0k2 |
, получим равновесные концентрации веществ А |
||||
k1 |
|
||||||
t |
k2 |
|
|
|
|
|
|
и В.
Найдем произведение константы скорости k1 прямой стадии на равновесную концентрацию вещества А и произведение константы скорости k2 обратной стадии на равновесную концентрацию вещества В.
Указанные произведения совпадают. Это означает, что скорости прямой и обратной стадий двусторонней реакции первого порядка со временем становятся практически одинаковыми, что соответствует состоянию динамического равновесия системы.
2. Рассмотрим математическую модель двусторонней реакции второго порядка. Так же, как и в первом случае, получим аналитическое решение задачи Коши из данной математической модели при помощи метода разделения переменных с последующим интегрированием.
77
