Degtyarenko_dlya_studentov_II_kursa_2013 / Детерминир. модели / Лекции Дет. модели. Часть 2

На рисунке изображены графики кинетических кривых, полученных для гипотетических реакций различных порядков (n 1,2,3), характеризующихся одними и теми же числовыми значениями константы скорости реакции и начальной концентрации реагирующего вещества.

2. При построении математической модели для случая 2 было показано, что она аналогична модели для случая 1, где n 2. Воспользуемся ранее полученными результатами и выразим текущие концентрации CA t CB t через время и заданные константы, предварительно «очистив» переменные CA0 и k от введенных ранее конкретных значений.

Получены уравнения кинетических кривых для случая 2: CA t CB t

CA0 / 1 ktCA0 (этот результат обозначен в программе sol4). Пред-

ставим кинетические кривые графически.

58

3. Снова «очистим» переменные CA0 и k от введенных ранее конкрет-

ных значений. Найдем интегралы из левой и правой частей равенства

данные в условии константы.

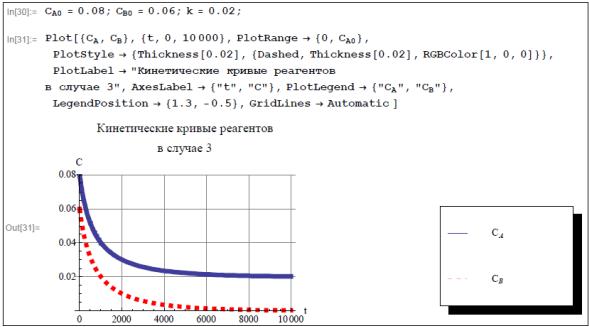
Согласно построенной в пункте 3 математической модели получим текущие концентрации CA t ,CB t реагентов.

Представим графически аналитическое решение прямой кинетической задачи, полученное при рассмотрении случая 3, задав конкретные числовые значения начальных концентраций реагирующих веществ и константы скорости реакции.

59

Упражнение. Важной характеристикой простой реакции, реакционная схема которой приведена в пункте 1, является период полупревращения, т. е. время с момента начала реакции, за которое начальная концентрация реагента сокращается в два раза. Для каждого из случаев n 1,2,3 установите связь между периодом полупревращения и исходной концентрацией реагента. Получите эти закономерности при помощи компьютерной системы Mathematica. Заметим, что указанные закономерности используют на практике при установлении порядка исследуемой реакции по экспериментальным данным.

4. Анализ полученных результатов. В соответствии с принци-

пами химической кинетики получены аналитические решения прямых кинетических задач, сформулированных в пунктах 1, 2, 3. Эти решения представлены также и графически. Все графики выглядят однотипно (монотонно убывающие, вогнутые на рассматриваемых промежутках). Докажем, например, для случая 3, что графики обеих текущих концентраций CA t ,CB t являются монотонно убывающими и вогнутыми на промежутке t 0 при любых положительных значениях констант k,CA0,CB0 CA0 CB0 .

Прежде всего, отметим, что при любом значении t 0 соответствующие значения функций CA t ,CB t отличаются друг от друга на постоянную величину. Это следует из формул

В связи с этим проведем исследование, например, функции CA t при помощи ее первой и второй производных, а затем распространим результаты этого исследования на функцию CB t .

Первая производная указанной функции отрицательна при t 0. Следовательно, график функции – монотонно убывающий на рассматриваемом промежутке.

Вторая производная функции положительна при t 0. Следовательно, график функции – вогнутый на рассматриваемом промежутке.

Результаты проведенного математического исследования функции CA t кратко можно представить в виде схемы, изображенной на рис. 2.4.1.

Исследование функции при помощи ее первой производной показывает, что при t 0 текущая концентрация реагента А монотонно убывает. С химической точки зрения первая производная функции характеризует скорость изменения текущей концентрации реагента. Исследование функции при помощи второй производной показывает, что первая производная является монотонно возрастающей функцией при t 0. Следу-

61

ет заметить, что первая производная отрицательна при t 0, значит, ее монотонное возрастание означает монотонное убывание в абсолютном смысле. Это обстоятельство отражает и график функции, который является вогнутым при t 0, и, следовательно, одинаковым изменениям переменной t с ростом аргумента соответствуют все меньшие по модулю изменения значения функции CA t . Таким образом, в химическом смысле скорость изменения текущей концентрации реагента А монотонно убывает при t 0.

В качестве упражнения проведите аналогичные исследования функциональных зависимостей текущих концентраций реагентов от времени в случаях 1 и 2. В случае 1 можно заметить, что с повышением порядка реакции убыль концентрации реагента во времени становится менее интенсивной. С помощью полученных в пунктах 1, 2, 3 аналитических выражений можно строить кинетические кривые для различных веществ, задаваясь конкретными числовыми значениями их начальных концентраций, а также значениями констант скоростей простых реакций.

Замечание 1. В данном подразделе мы обсуждали вопросы кинетики реакций различных порядков, во многом рассматривая понятие порядка как формальную величину, не «привязываясь» к конкретным примерам химических превращений. Именно, в этом и состоит особенность фор-

мально-кинетического (модельного) подхода к описанию реакций. Поря-

док реакции – это величина, которую нельзя рассчитать теоретически для конкретной реакции, ее можно установить только на основании данных, полученных из химического эксперимента. Практика показывает, что большинство реакций имеют первый или второй порядок. Крайне редкими являются реакции третьего порядка. Удобным зрительным образом химического взаимодействия является представление о столкновении реагирующих частиц в реакционной системе. Если представить такое столкновение как элементарный акт, приводящий к появлению продуктов реакции, то очевидно, что вероятность встречи двух частиц в некоторой точке пространства гораздо более высокая, чем вероятность столкновения трех частиц. По этой причине реакций второго порядка гораздо больше, чем реакций третьего порядка. О возможности осуществления реакций более высоких порядков говорить вообще не приходится.

Замечание 2. Знание порядка отдельной реакции еще ничего не говорит о механизме, по которому она протекает. Например, если экспериментально определен первый кинетический порядок реакции, это отнюдь не означает, что исследуемая реакция является простой. Экспериментально определяемый порядок может указывать на то, что исследуемая

62

реакция является сложной, а поведение системы определяется некоторой лимитирующей стадией, которая имеет порядок, определенный опытным путем. Также экспериментально определяемый порядок может оказаться псевдопорядком. Рассмотрим в качестве примера реакционную схему

k

A B Продукты в предположении, что начальная концентрация реагента B настолько больше начальной концентрации реагента A, что изменением концентрации B в ходе реакции можно пренебречь и счи-

тать, что CB(t) const. Тогда dCA(t) kCA(t)CB(t) k CA(t). В данном dt

случае константа k включает в себя практически не изменяющуюся во времени концентрацию вещества B и называется эффективной константой скорости в отличие от истинной константы скорости k . Изменение концентрации реагента A соответствует закономерностям реакции первого порядка, но при этом говорят, что реакция имеет псевдопервый порядок.

Замечание 3. Однозначно можно утверждать, что наличие дробного или отрицательного порядка реакции свидетельствует о сложном механизме ее протекания. Некоторые реакции имеют нулевой порядок. Такая величина порядка характерна либо для сложных реакций, либо для простых реакций, идущих по особому механизму, обеспечивающему такие энергетические условия взаимодействия реагирующих частиц, при которых скорость реакции не зависит от концентрации.

4.3.Простая перегонка

1.Постановка задачи. Смесь бензол-толуол подвергают простой перегонке, при которой в перегонный куб непрерывно с постоянной скоростью v (кмоль/ч) поступает жидкая смесь, мольная доля бензола в которой равна c. Предполагается, что количество жидкой смеси, находящейся в перегонном кубе, не меняется с течением времени и равно некоторому начальному количеству a (кмоль), т. е. скорость v поступления смеси равна скорости отвода паров. Известно, что к моменту t0 ус-

тановления динамического равновесия процесса начальная мольная доля бензола в жидкости, находящейся в перегонном кубе, равна x0, а при описании динамического равновесия процесса могут быть использованы законы Рауля и Дальтона. Установите, какое время (ч) потребуется для того, чтобы содержание бензола в парах над жидкой смесью, выраженное в мольных долях, было равно y1.

63

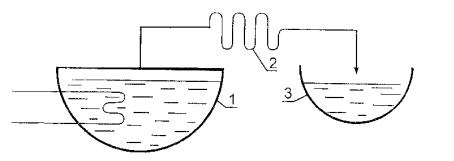
2. Математическая модель. Процесс простой перегонки осуществляют по схеме, изображенной на рисунке 2.4.2, где 1 – перегонный куб, 2 – конденсатор, 3 – приемник дистиллята.

Рис. 2.4.2

Математическая модель этого процесса базируется на принципе материального баланса. Введем следующие обозначения: x(t) – мольная доля бензола в жидкости, находящейся в перегонном кубе, в момент времени t (t t0); y(t) – мольная доля бензола в парах над жидкостью, находящейся в перегонном кубе, в этот же момент времени t. Из условия следует, что началу процесса соответствует время t0. Рассмотрим временной отрезок t;t t , где t t0; t 0, t 0. Исходя из наших обозначений, ax(t t) – это количество бензола в жидкости, находящейся в перегонном кубе, в момент времени t t, а ax(t) – это количество бензола в жидкости в момент времени t. Для построения математической модели процесса простой перегонки воспользуемся принципом материального баланса, который заключается в том, что количество ax(t t) равно количеству ax(t) плюс приход бензола в жидкость, находящуюся в перегонном кубе, за время t и минус убыль бензола из жидкости за это же время:

ax(t t)=ax(t) v tc v ty(t), t t0; t 0, t 0.

Перепишем это уравнение в дифференциальной форме:

При описании динамического равновесия в данном случае могут быть использованы законы Рауля и Дальтона. Согласно им можно записать формулу, выражающую связь между величинами x(t) и y(t) (t t0):

1 ( 1)x(t)

64

функцию y, выраженную через функцию x, в (2.4.1), получим дифференциальное уравнение с разделенными переменными

Обозначим время (ч), которое необходимо найти по условию задачи, через t1. Согласно условию y t1 y1 и x t0 x0. Содержание y1 бензола в парах над жидкой смесью, выраженное в мольных долях, соответствует содержанию x1 (в мольных долях) бензола в жидкости, находящей-

циальное уравнение (2.4.2), расставив пределы интегрирования в определенных интегралах следующим образом:

Остается вычислить определенный интеграл и выразить необходимое нам время t1 через заданные в условии постоянные и 2,48.

3. Решение математической модели средствами компью-

терной системы Mathematica. Приведем фрагменты программного кода, снабженные пояснениями и комментариями. Поскольку подынтегральное выражение в формуле (2.4.3) содержит числовые параметры, использование встроенной функции Integrate для вычисления определенного интеграла нецелесообразно. Как правило, ее применяют для вычисления определенных интегралов в тех случаях, когда подынтегральная функция и пределы интегрирования не содержат неопределенных числовых параметров. Поэтому сначала при помощи встроенной функции Integrate найдем соответствующую первообразную, а затем запрограммируем формулу Ньютона – Лейбница для отыскания опреде-

Теперь по формуле (2.4.3) выразим время t1 (в программе оно обозначено time) через заданные в условии постоянные и .

Присвоим постоянным конкретные числовые значения и учтем, что2,48. Реализуем математическую модель процесса простой перегонки с помощью системы Mathematica тремя способами: в соответствии с описанным выше алгоритмом, вычисляя определенный интеграл при помощи команды Integrate, используя встроенную функцию NIntegrate. Убедимся в идентичности полученных результатов.

66

4. Анализ полученных результатов. Полученное в общем ви-

де решение имеет место, если выполняется ряд условий. Так, из его сле-

1

ной доли бензола в жидкой смеси. Также, согласно полученной формуле решения, y1 y1 0;c y1 0. Эти условия следуют из математиче-

средствами системы Mathematica символьная форма решения поставленной задачи корректна с математической точки зрения и адекватна химическому содержанию задачи при выполнении условий c cx0 x0 c x0 0,t1 t0.

5. АНАЛИТИЧЕСКОЕ И ЧИСЛЕННОЕ РЕШЕНИЕ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ И ИХ СИСТЕМ В РЯДЕ ЗАДАЧ ХИМИЧЕСКОЙ КИНЕТИКИ

5.1. Двухстадийные реакции, протекающие в закрытых системах

5.1.1. Обратимые (двусторонние реакции)

1. Постановка задачи. Рассмотрите прямую кинетическую задачу для случаев протекания обратимых реакций в закрытой изотермической системе (объем и температура постоянны) в предположении, что имеет место соответствие между кинетическим и стехиометрическим уравнениями реакции. Получите аналитическое решение прямой кинетической задачи, т.е. уравнения кинетических кривых. Представьте полученное решение графически. Проанализируйте результаты с химической точки

67