24.Метод локального поиска и поиска с запретами. Задача о максимальном разрезе.

Алгоритм локального поиска:

Идея: Построить какое-то решение и стараться его улучшить до тех пор, пока это возможно.

1) Для каждого решения S задачи определим его окрестность N(S) – мн-во решений близких к S.

2) Найдём какое-то начальное решение S₀.

3) Посмотрим решения из N(S₀), если найдем решение S 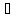N(S₀), такое что w(S) < w(S₀), то положим S= S₀ и снова повторим 3, если не найдём , то стоп. Фактически алгоритм локального поиска ищет локальный оптимум. Качество этого алгоритма зависит от того, как определяются окрестности решений.

Алгоритм 2-замены для задачи о коммивояжере.

Вибираем два несмежных ребра и заменяем их другими так чтобы снова получился гамильтонов цикл, всего таких соседей: n(n-3)/2 – число способов выбрать 2 пары вершин из всех.

Локальный поиск для задачи о max разрезе.

Вход: граф G=(V,E)

Найти: рабиение мн-ва V на 2 подмн-ва A и B такое, что число рёбер между A и B максимально.

Мн-во решений – все разбиения (A,B), окрестность решения (A,B) – это все разбиения вида: (A\{v}, B объединение {v}) и (A объединение{v}, B \{v}).

Т-ма. Алгоритм локального поиска для задачи о макс разрезе имеет гарантированную оценку точности 2.

Док-во. Пусть m число ребер графа G, opt – оптимальное решение задачи, k – решение задачи, найденное алгоритмом локального поиска. Очевидно, что opt≤m, поэтому достаточно показать, что k≥m/2. Пусть (A,B) – найденное алгоритмом разбиение, m_a – число ребер, оба конца которых лежат в A, m_b – число ребер, оба конца которых лежат в B. m= m_a+ m_b+k

v – вершина графа , N_a(v) – вершины смежная с v, которые лежат в A, N_b(v) - вершины смежная с v, которые лежат в B.

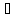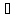Т.к. (A,B) – локальный оптимум, то дляv A, | N_a(v)| ≤ |N_b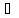(v)|. v 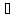B, | N_b(v)| ≤ |N_a(v)|.

Просуммируем эти неравенства по всем v 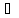A и по всем v 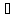B.

∑_{v из A}| N_a(v)|-∑_{v из A}| N_b(v)|=2m_a-k≤0

∑_{v из B}| N_b(v)|-∑_{v из В} N_a(v)|=2m_b-k≤0

Сложим оба выражения, получим: m_a+ m_b-k≤0.

m= m_a+ m_b+k

m_a+ m_b=m-k

m-2k≤0.

Алгоритм поиска с запретами(Tabu search)

Позволяет алгоритму выбраться из локального оптиума

Пусть алгоритм локального поиска за последние r шагов построил решение s_i-r , s_i-r+1 ,…..s_i , s_j+1 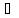N(s_j) для решения s_i определяет список запретов Tabu(s_i). Следующее решение s_i+1 ищем как лучшее решение из множества N(s_i)\ Tabu(s_i) Множество Tabu(s_i) определяется по r предыдущем решений таким образом, чтобы исключить из рассмотрения те фрагменты решений , которые уже меняются на последних шагах алгоритмов.

Пример Задача о раскраске графа

Вход: граф G=(V,E) и нат. число k.

Вопрос: можно ли раскрасить вершины графа в к цветов? (можно ли разбить мн-во вершин графа на k нез. мн-в?)

Решения – все функции c:V(G) ® {1,2,…,k}

Вход: граф G=(V,E) и натуральное число k

Найти: функцию c_opt:V(G) ® {1,2,…,k}такую, что

w(c_opt) = |{uvÎE(G) : c(u)=c(v)}| минимальна количество ребер, концы которых покрашены в один цвет, минимально.

Пусть с=(с₁,…,с_n) – некоторое решение .Окрестность N(c) – это множество функций c’ = (c’₁,…,c’_n), получающихся из c следующим образом: берем ребро abÎE такое,что с(a)=c(b)и перекрашиваем вершину a в другой цвет. Пусть мы перекрасили вершину a в цвет i_i Tabu на ближайшие r итераций – множество функций с таких, что с(a) = i Tabu на ближайшие r итераций – множество раскрасок, в которых 1 покрашена в красный цвет