22. Np- полные задачи. Теорема Кука-Карпа-Левина. Np-полнота задачи о клике

Задача называется NP-полной, если к ней полиномиально сводится любая задача из NP.

Если хотя бы одна NP-полная задача полиномиально разрешима, то P = NP

NP-полные задачи – это самые сложные задачи (не удастся найти для неё полиномиальный алгоритм) Если А – NP- полная и AB, то В – NP- полная

1)Задача “3-Выполнимость”

Вход: булева функция f(x₁,…,x_n), заданная в виде КНФ, причем все ЭД содержат ровно 3 переменные.

Вопрос: существует ли такие x₁,…,x_n , что f(x₁,…,x_n)=1?

2)Задача “Клика”

Вход: граф G и натуральное число k

Вопрос: содержит ли граф клику размера k?

3)Задача “Вершинное покрытие”

Вход: граф G и натуральное число k

Вопрос: содержит ли граф вершинное покрытие размера k?

4)Задача “3-мерное сочетание”

Вход: Множество MXYZ, |X|=|Y|=|Z|=q

Вопрос: существует ли подмножество NM такое, что |N| = q и никакие два элемента из N не имеют ни одной равной координаты (т.е. для любых (a,b,c), (u,v,w)N,a≠u,b≠v,c≠w)?

5)Задача “Гамильтонов цикл”

Вход: граф G

Вопрос: существует ли цикл, проходящий через каждую вершину графа ровно 1 раз (гамильтонов цикл)

6)Задача “Разбиение”

Вход: массив X из n натуральных чисел x₁,…,x_n

Вопрос: можно ли разбить X на два подмассива Y и Z таких, что суммы их элементов равны?

Задача “Выполнимость”

Вход: булева функция f(x₁,…,x_n), заданная в виде КНФ

Вопрос: существует ли такие x₁,…,x_n , что f(x₁,…,x_n)=1?

Теорема Кука-Карпа-Левина. Задача “SAT”(Задача “Выполнимость”) является NP-полной.

Теорема. Задача “Клика” является NP-полной.

Доказательство.

Докажем сначала, что “Клика”NP. Сведем к задаче “Клика” задачу “3-выполнимость”. Пусть F= C₁&…&C_k – вход задачи “3-выполнимость”,

где С_i – это ЭД.

Литерал – это либо переменная, либо отрицание переменной.

Каждая ЭД C_i содержит ровно 3 литерала. Посторим граф G следующим образом.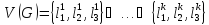 и 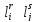если и только если rs и литералы, соответствующие этим вершинам, не являются отрицаниями друг друга.

Теперь нам нужно показать, что F выполнима тогда и только тогда, когда в построенном графе есть клика порядка k. Пусть F выполнима. Тогда после подстановки соответствующего набора переменных в каждой ЭД должен быть истинный литерал. Пусть это литералы 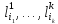. Покажем, что 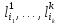- клика. Действительно, все эти литералы взяты из разных ЭД. Кроме того, они все равны 1 => никакие 2 из них не могут быть отрицаниями друг друга.

Обратно, пусть в построенном графе есть клика порядка k. Эта клика содержит ровно по одной вершине из каждой тройки. Если литерал, соответствующий вершине клики – это отрицание, то присвоим соответствующей переменной значение 0. Если же этот литерал – не отрицание, то присвоим значение 1. Могло бы получиться противоречие, если бы в клику входили два литерала, один из которых равен x₁, а другой – отрицанию x₁. Но такого не будет по определению графа.

23. Алгоритмы с гарантированной оценкой точности. Задача упаковки

Эвристические алгоритмы(полиномиальный алгоритм, находящий приближенное решение)

Пусть А – алгоритм решения задачи, заключающийся в нахождении X_opt такого, что f(X_opt) минимально.

Алгоритм А имеет гарантированную оценку точности k, если для любого найденного алгоритмом решения Х f(X) <= kf(X_opt).

Задача упаковки.

Вход: мн-во из n предметов с весами w₁,…, w_n, где w_i  (0, 1].

Нужно упаковать предметы в мин. число контейнеров единичной емкости.

Теорема. Задача упаковки является NP-трудной.

Док-во. Докажем, что «разбиение» ( полиномиально сводится к ) «упаковке». Пусть U=(w₁,…, w_n) – вход задачи «разбиение». Можно без ограничений общности считать, что w _i  (0, 1] (в противном случае разделим все w_i на w = max{w_j}).

Положим c = |1/2 * ∑w_i|, i=1,…, n и преобразуем U во вход V=(w₁/c,…, w_n/c) задачи «упаковка».

Легко видеть, что U можно разбить на 2 подмассива с одинаковыми суммами элементов iff когда предметы из V можно упаковать в 2 контейнера.

Пусть предметы можно упаковать в два контейнера.

Пусть I и J – мн-ва индексов предметов упакованных в 1 и 2 контейнерах.

Имеем:

∑(w_i/c)(iI) ≤ 1, ∑(w_j/c)(jJ) ≤ 1,

∑w_i (iI) ≤ c, ∑w_j(jJ) ≤ c

∑w_i (iI) ≤ 1/2*∑w_i (i=1,…, n), ∑w_j (jJ) ≤ 1/2*∑w_i (i=1,…, n)

Пусть теперь массив U можно разбить на 2 подмассива с одинак. суммами эл-ов. Пусть I и J – мн-ва индексов эл-ов из первого и второго подмассивов.

∑w_i (iI) = 1/2*∑w_i (i=1,…, n), ∑w_j (jJ) = 1/2*∑w_i (i=1,…, n),

∑(w_i/c)(iI) = 1, ∑(w_j/c)(jJ) = 1

Алгоритм Следующий подходящий(NF)

В произвольном порядке упаковываем по следующему правилу : первый предмет помещаем в первый контейнер. На k – шаге пытаемся поместить k-ый предмет в текущий контейнер ,если предмет входит ,то помещаем его , если нет пытаемся в другой контейнер Трудоемкость : О(n)

Т-ма NF имеет гарантированную оценку точности 2

Док-во пусть w = w₁+…+ w_n и Т₁,…….,Т_n – контейнеры, найденные алгоритмом, opt- оптимальное число контейнеров

opt 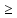w .Пусть w(T_i) – общий вес предметов , упакованных в i – ый контейнер w = (w(T₁) + w(T₂))+ (w(T₃) + w(T₄))+ … сумма весов предметов , упакованных в 2 подряд идущих контейнера >1

W > k/2, opt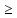 W > k/2

Алгоритм Первый подходящий (FF)

В произвольном порядке упаковываем предметы по следующему правилу: первый предмет помещаем в первый контейнер. На k–шаге находим контейнер с наименьшим номером, куда помещаем k-ый предмет. Если такого контейнера нет , то берем новый контейнер и помещаем предмет в него. Трудоемкость : О(n²)

Т-ма FF находит упаковку в не более чем 17/10 Opt + 1 контейнер

Алгоритм Первый подходящий с упорядочиванием (FFD)

Сортируем алгоритм по не возрастанию весов и применяем алгоритм FF(NF)

Т-ма FFD находит упаковку в не более чем 11/9 Opt + 4 контейнера

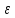
Утв Если для какого-то 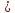0 для задачи упаковки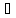приближенный полиномиальный алгоритм с гарантированной оценкой точности 3/2 –, тоP = NP

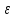
Док-во пусть алгоритм А для задачи упаковки с гарантированной точностью 3/2 – Мы покажем , что задача Разбиение сводится к задаче упаковки в 2 контейнера. Рассмотрим задачу упаковки в 2 контейнера. Пусть алгоритм А получает на входе задачу упаковки ,правильный ответ котором - 2. Какой ответ на этом входе даст алгоритм А? Если А даст ответ 3, то этот ответ в 3/2 раза хуже оптимального!