10 .Поиск в ширину(волновой алгоритм)

Метка вершины – ее расстояние до начальной вершины.

Первой вершине метка 0,смежным с ней – 1, смежным с 1 -2 и тд. С помощью очереди заносим новые вершины (если в буквах) и удаляем те которые уже исследованы.

Трудоемкость – O(n+m)

Применение:

1. Проверка связности графа

2. Распознавание деревьев (дерево – связный граф без циклов)

Утверждение. В графе нет циклов тогда и только тогда, когда в ходе выполнения алгоритма поиска в ширину каждая вершина исследуется на предмет необходимости присвоения ей метки ровно один раз.

Множество вершин графа называется независимым,

если все вершины из этого множества попарно несмежны.

Граф называется двудольным, если множество его

вершин можно разбить на два независимых множества

(доли)

Теорема. Граф является двудольным если и только

если он не содержит циклов нечетной длины

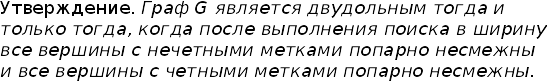
11.Поиск в глубину

1.Выбираем вершину v₀. Помечаем ее как текущую. Полагаем D(v₀) = 1, k = 1.

i.Пусть x – текущая вершина.

i.1.Если существует непомеченное ребро xy, то а) если y уже имеет номер, то помечаем ребро xy как обратное и продолжаем поиск непомеченного ребра, инцидентного x б) если y не имеет номера, то k++, D(y) = k, переходим в y.

i.2. Если непомеченного ребра xy не существует, то возвращаемся в вершину, из которой x получила свою метку.

k:=1, v:=v₀, D(v):=k; push(Q,v), D(v):=-1 "uÎV(G)\{v}

while (Q¹Æ)

{

с = false;

v:=top(Q);

for (uÎN(v))

if (D(u)=-1)

uv – прямое; k++; D(v)=k; push(Q,u);

c = true; break;

else

uv – обратное

if (!c)

pop(Q);

}

Утверждение 1. Прямые ребра образуют корневое остовное дерево с корнем в начальной вершине.

Утверждение 2. Обратное ребро направлено от вершины с большей меткой к вершине с меньшей меткой.

Применение поиска в глубину:

Проверка графа на связность, на двусвязность.

Граф называется двусвязным, если между любыми двумя его вершинами существуют два непересекающихся пути . Двусвязная компонента графа (или блок) – максимальный двусвязный подграф графа.

Трудоемкость - O(n+m)

Утв. Пусть V не явл-ся корнем. Тогда V точка сочленения  для некоторого ее сына s не существует ребра (x,y) что х – потомок s или =s, а y – предок V.

12.Жадные алгоритмы и матроиды

E – конечное множество, w: E ® R₊

Для XÍ E w(X) = 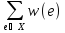, IÍ B(E) , w(X) ® min (max) , XÎ I

Жадный алгоритм

1.Выбираем элемент x₁ максимального веса такой, что {x₁}Î I.

2.Выбираем элемент x₂Î E\{x₁} максимального веса такой, что {x₁,x₂} Î I

i.Выбираем элемент x_i Î E\{x₁,…,x_i-1} максимального веса такой, что

{x₁,x₂,…,x_i-1,x_i} Î I

Матроид – это пара (X,B), где X – конечное множество, а B – непустое множество его подмножеств (элементы B - базы), удовлетворяющая следующим условиям:

1.Никакая база не содержится в другой базе (аксиома максимальности);

2.Если B₁ и B₂ – базы, то для любого элемента bÎ B₁ 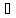элемент сÎ B₂ такой, что B₁\{b}È{c} – база.

Матроид – это пара (X,I), где X – конечное множество, а I – непустое множество его подмножеств (элементы I - независимые множества), удовлетворяющая следующим условиям:

1.Для любого I₁Î I и I₂Í I₁ I₂ Î I

2.Если I₁ и I₂ – независимые множества и |I₁| < |I₂|, то 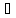элемент сÎ I₂\I₁ такой, что I₁È{c} Î I

Пара (X,I), для которой выполняется аксиома 1) – система независимости

Примеры матроидов

1/(X,{X})

2.X – конечное множество векторов некотороговекторного пространства, B – максимальные линейно независимые системы векторов из X (базисы X).

3.X – множество ребер некоторого графа G,B – подмножества ребер, составляющих остовные деревья G.

Теорема. Жадный алгоритм, примененный к системе независимости (E,I), всегда находит оптимальное решение тогда и только тогда, когда (E,I) – матроид.