25.Метод ветвей и границ. Задача коммивояжера.

Задача коммивояжёра. Задан граф G, каждому ребру соотв. его вес. Найти в G гамильтонов цикл (через все вершины) мин. веса.

Утв. Эта задача NP-трудная, «гамильтонов цикл» « коммивояжер».

Теор. Если для какой-то константы r 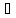полиномиальный алгоритм решения задачи коммивояжёра с гарантированной оценкой точностиr, то P=NP.

Док-во. Пусть такой r и алгоритм А 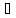Рассм. задачу «гамильтонов цикл», пусть графG =(V,E) её вход, |G| = n. Построим вход задачи коммивояжёра определив веса ребер следующим образом: c_ij = .

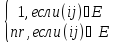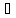путь коммивояжёра длины n iff в G есть гамильтонов цикл. Если алгоритм 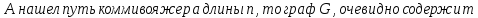гамильтонов цикл. Если длина пути, найденного этим полиномиальным алгоритмом, большеn, то она не меньше nr+(n-1), поскольку включает хотя бы одно ребро веса nr(тяжелые ребра). Но поскольку алгоритм, по условию, ошибается не более чем в r раз, то получается что длина оптимального пути коммивояжера > n =>в G нет гамильтонова цикла .Получили что в G есть гамильтонов цикл iff алгоритм А может найти путь коммивояжера длины n за полиномиальное время => P=NP.

Метод ветвей и границ. Мы решаем задачу Х. S – мн-во всех возм. решений задачи Х. Нам нужно найти решение s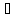S такое, что w(s) минимально. Строим дерево решений. Для какого-то мн-ва решений Т пусть g(T) – нижняя оценка для стоимостей решений из Т, т.е. такое число, что w(s)g(T) для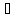решенияs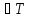Предп., что мы умеем генерировать нижние оценки g для любой вершины дерева решений. Возьмём произв. решение и запомним его стоимость это будет текущий рекорд record.

Для решения задачи коммивояжёра надо знать:

1. Как ветвить дерево решений

2. Как генерировать нижние оценки

Пусть S – мн-во всех гамильтоновых циклов, ij – нек. ребро. Разделим S на 2 части, одна содержит ребро ij, другая нет. И т.д.

Задачу коммивояжера можно задать с помощью матрицы

С_ij стоимость (вес) ребра ij

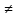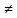Пусть ОРТ(С_ij) – оптимальное стоимость пути для задачи коммивояжера, заданной при помощи матрицы С , введем обозначение а_i = min c_ij , i j , i=1,..,n , b_j = min (c_ij - а_i), i j , j=1,..,n

Т-ма ОРТ(С_ij) +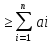

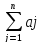
26. Задача коммивояжера с неравенством треугольника. Алгоритм Кристофидеса

Задано множество городов V и для каждой пары городов u и v – стоимость проезда из u в v. Коммивояжер должен объехать все города, затратив на это минимально возможную сумму денег.

Метрическая задача коммивояжера

с(x,y)£c(x,z)+c(z,y)

Алгоритм Кристофидеса

Идея: дополним граф до эйлерова графа, добавив новые кратные ребра таким образом, чтобы степени всех вершин стали четными. Найдем в полученном графе эйлеров цикл H. Если в H каждая вершина встречается ровно 1 раз, то это гамильтонов цикл. Пусть вершина x встречается 2 раза …-u-x-v-… - второе вхождение x. Заменим в H ребра ux и xv на ребро uv, получив

новый цикл H’ .c(u,x)+c(x,v)£ c(uv), следовательно, с(H’) £c(H) Проделав это со всеми кратными вхождениями вершин, в конце концов получим гамильтонов цикл H’ такой, что с(H’)£c(H) Проделав это со всеми вершинами , в конце концов мы получим гамильтонов цикл H’,т.что с(H’)£c(H)

Какие ребра надо было добавлять вначале, чтоб когда добавляли нашелся эйлеров цикл?

//не знаю что это но не удаляла

(1. Находим минимальное остовное дерево T графа G

2. Пусть U – множество вершин T, имеющих нечетную степень, G[U] – подграф графа G, порожденный U. Найдем в G[U] совершенное паросочетание минимального веса

3. Добавим к дереву T все ребра M, если какое-то ребро из M там уже есть, то добавим кратное ему. Получим эйлеров граф, содержащий все вершины графа G. Найдем в нем эйлеров цикл H и “сожмем” его до гамильтонова цикла H’)