
уч.пос.1 (1)
.pdfФЕДЕРАЛЬНОЕ БЮДЖЕТНОЕ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«БАШКИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»
К.П. Исаев, О.А. Кривошеева, Р.С. Юлмухаметов
ДИСКРЕТНАЯ МАТЕМАТИКА ЧАСТЬ 1
Учебное пособие
Уфа РИЦ БащГУ
2014
УДК 510.22
ББК 22.1
В учебном пособии «Дискретная математика. Часть 1» изложе-
на часть материала, предусмотренного Государственным стандартом по дисциплинам «Дискретная математика» и «Дискретная математика и математическая логика» по направлениям «Прикладная математика и информатика», «Математика» и «Прикладная информатика». Пособие включает следующие разделы дисциплины: 1) основы теории множеств; 2) комбинаторика; 3) отображения и отношения. По данным разделам приведены основные теоретические сведения, разбор типовых задач,
тестовые задания и варианты контрольных работ для самостоятельного решения с целью закрепления пройденного материала.
2
СОДЕРЖАНИЕ
1. Множества. Операции над множествами.
Теоретические сведения…………………………………..………………4
Разбор типовых задач……………………………………………………..7 2. Комбинаторика.
Теоретические сведения…………………….…………..………………..10 Разбор типовых задач………………………………….…………………11
3. Бинарные отношениях на множествах.
Теоретические сведения………………………….………………………17
Разбор типовых задач…………………………….………………………17
4. Отображения.
Теоретические сведения………………..……….………………………..18 Разбор типовых задач………………………….…………………………19
5. Мощность множества Теоретические сведения……………………….…………………………22
Разбор типовых задач………………………….…………………………23
6. Задачи для самостоятельного решения.
Задача №1………………………………………………………………….25 Задача №2……………………………………………….…………………31 Задача №3………………………………………………………………….32 Задача №4………………………….………………………………………35
Задача №5………………………………………………………………….37 Задача №6……………...…………………………………………………..45 Задача №7……………………….…………………………………………47 Задача №8………………………………………………………………….48 Задача №9…………………...……………………………………………..49 Задача №10………………..……………………………………………….51 Задача №11………………..……………………………………………….53
Задача №12…………………..…………………………………………….57
Задача №13………………….……………………………………………..58 Задача №14………………………..……………………………………….64
Задача №15…………………………………………...……………………70
Задача №16…………………….…………………………………………..72 Задача №17………………………..……………………………………….73 7. Типовые варианты контрольных работ…...…………………………..74
3
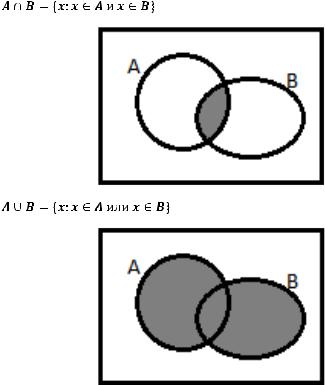
Разбор типового варианта.
1. Множества. Операции над множествами.
Теоретические сведения:
Основные операции:
4
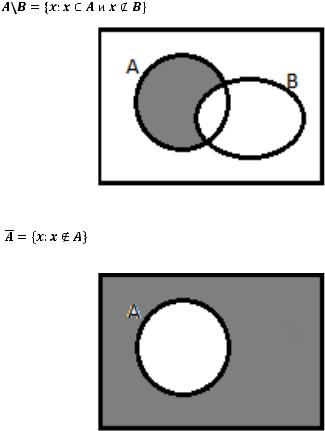
5
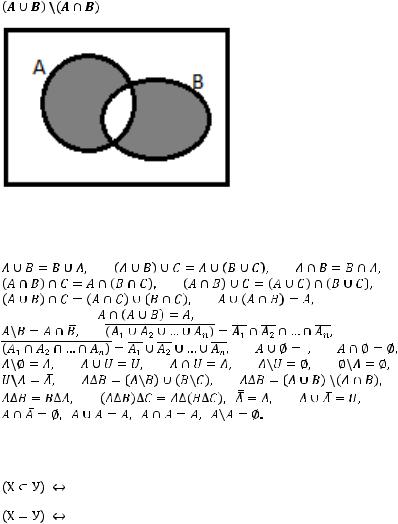
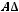
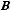

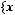


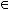


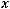
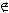
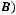
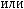
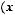
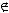
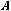

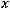
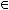

 =
=
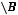 )
) 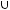
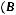
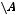
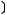

Свойства операций ( - универсальное множество):
- универсальное множество):
Включения и равенство множеств:
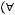

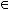
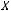
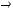

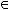
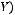 .
.
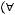

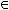
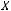
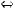

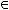
 .
.
Если 
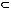
 и
и 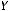

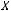 , то
, то 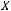

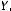 Если
Если 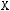
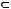
 и
и 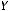
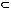
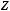 , то
, то 

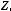
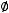
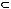
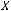

 множества
множества  .
.
6
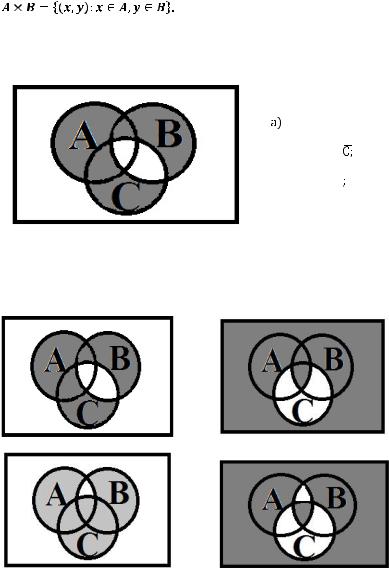
Декартово произведение двух множеств:
Задача №1. Определите, какое множество заштриховано на рисунке:
Варианты ответов:
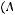
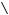

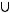
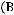
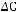
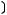 ;
;
б) 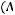

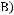
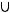
в) 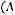
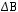
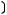
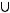
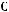
г) 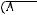
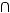
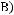
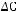 .
.
Решение:
Изобразим множества из вариантов ответов:
а) |
б) |
в) |
г) |
Ответ: а)
7

Задача №2. Даны множества: А=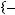
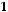

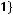 , В=
, В=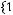

 С=
С=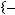
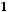
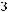
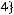
 Найти сумму элементов множества
Найти сумму элементов множества 
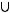
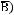
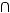
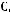
Решение:
Сумма равна 6.
Ответ: 6.
Задача №3. Выбрать множество равное множеству 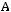

 :
:
а) 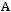
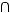
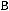 ; б)
; б) 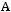
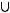
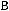
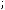
в) г)
Решение:
Ответ: а)
Задача №4. А,В,С- произвольные множества. Х=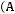
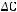
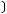
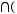
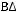
 , У=
, У= 
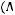
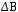
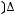
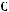 . Выберите верный вариант ответа:
. Выберите верный вариант ответа:
а) Х=У; б) 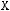
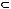
 в) Х У;
в) Х У;
г) нет верного ответа.
Решение:
Нарисуем множество Х и множество У.
8
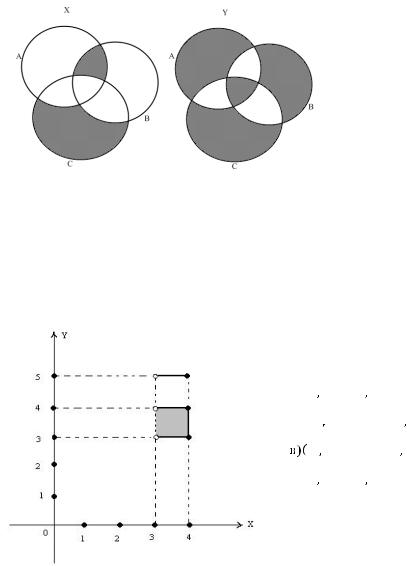
Из рисунка видно, что ни одно множество не является подмножеством другого.
Ответ: г)
Задача №5. Определите, какое множество заштриховано на рисунке:
а) 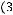
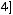

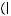
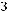
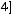




б) 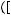
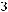
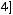

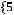


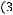
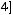

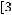
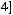
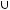
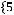
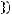

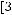
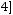 ;
;
г) 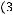
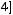

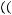
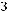

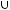
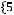
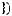

Решение:
Множество является объединением двух частей:
9

То есть 
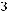
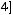

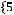
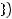
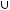
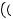
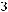


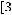



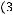




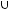

Ответ: а)
2. Комбинаторика.
Теоретические сведения:
Количество перестановок из n элементов: 
Число перестановок из |
объектов первого типа, |
объектов второго |
|||
типа, …, |
объектов k-го типа: |
|
|
. |
|
|
|
||||
Количество способов расставить n различных объектов по кругу равно
Количество способов связать бусы из n разноцветных бусинок равно



 .
.
Упорядоченные разбиения называются размещениями. Число размещений без повторений из n элементов по k: 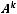

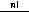

Число размещений c повторениями из n элементов по k: 

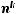

Неупорядоченные разбиения называются сочетаниями. Число сочетаний без повторений из n элементов по k: 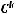

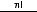

Число сочетаний c повторениями из n элементов по k: 

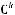

Количество упорядоченных разбиений множества, состоящего из n элементов, на k непересекающихся подмножеств, состоящих соответственно из  ,
, 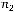 , …,
, …, 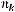 элементов (
элементов (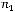

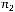


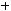
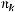

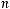 ):
):
.
10
