Тема 4. Алгебраические системы. Дистрибутивные решетки. Определение решетки, дистрибутивной решетки. Булева решетка. Алгебраические системы.

Множество М вместе с заданными на них операциями называется алгеброй.

Обозначается A=

Множество Mназывается основным, или несущим множеством, или просто носителем.

называется сигнатурой алгебры А.

Пример алгебры:

,

где множество M – множество натуральных чисел N;

–любая операция, в частности операция сложения.

Множество М вместе с заданными на нем отношениями называется моделью.

Обозначается

Например, моделью может быть множество с соотношением “быть больше или быть равным”M

Множество M вместе с заданными на нем операциями и отношенияминазывается алгебраической системой или алгебраической структурой.

Примеры алгебраической структуры:

Группоиды и полугруппы.

Алгебраическая система , гдесостоит из одной двухместной операции, как правило, операция умножения называется группоидом .

Операцию умножения не следует отождествлять с арифметической операцией умножения. Эту операцию можно выполнять над любыми двумя элементами V, причем эта операция не выходит за границы этого множества.

В случае конечного M группоид часто задают с помощью таблиц Кэли.

Пример:

Представим группоид таблицей Кэли:

, где (1)

	0	1	2	3	4
0	0	1	2	0	1
1	1	2	0	1	2
2	2	0	1	2	0
3	0	1	2	0	1
4	1	2	0	1	2

Примерыгруппоидов:

Множество всех целых чисел относительно операции вычитания. В то же время натуральные числа не образуют группоида относительно операции вычитания.

Группоид (1) называется идемпотентным, если

(2)

Группоид (1) называется коммутативным, если

(3)

Понятие группы.

Если для любых элементов группоида (1) имеет место ассоциативный закон:

(4),

то группоид U называется полугруппой или моноидом.

Если полугруппа обладает коммутативным свойством, т.е. ,

то полугруппу называют абелевой.

Группой называется алгебра (1),удовлетворяющая следующим условиям:

1)ассоциативности

2)существование нейтрального элемента или единичного элемента

3)существование обратного элемента

Условия (1), (2), (3) часто называют аксиомами группы.

Если дополнительно к этим условиям выполняется условие

4) коммутативности

,

то группу называют коммутативной или абелевой.

Пусть группоид задан таблицей Кэли

	a	b	c
a	b	c	a
b	c	a	b
c	a	b	c

Операция

1) ассоциативна

2) существует нейтральный элемент (в данном случае с)

3) для каждого элемента существует обратный элемент

Следовательно, рассмотренный группоид является абелевой группой, так как таблица Кэли симметрична относительно главной диагонали.

Группа называется конечной, если множество А конечно, в противном случае - бесконечной.

Число элементов в конечной группе называют ее порядком.

Кольца. Тела и поля.

Кольцом называется алгебра с двумя операциями, обладающими следующими свойствами:

1. Двойка есть абелева группа, нулевой элемент которой

2. Двойка 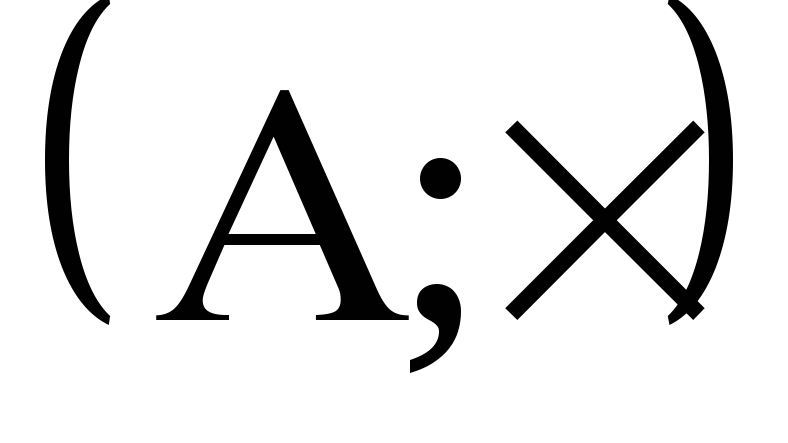-подгруппа

3. Операция дистрибутивна операции +, т.е.

Примером кольца может служить множество чисел, в котором выполняются операции сложения и умножения.

Кольца, в которых для всех отличных от нуля элементов, существуют обратные, называемые телами, иначе говоря, кольцо называется телом, если множество А, отличных от нуля элементов.

образует группу относительного умножения. В этом случае говорят, что в теле заданы 2 группы:

1) аддитивная

2)мультипликативная

Если мультипликативная группа абелева, то тело называется коммутативным, или полем.

Изоморфными называются объекты, которые имеют одну и ту же форму, одинаковое назначение и выполняют одинаковую функцию.

Два группоида , называются изоморфными между собой, если существует взаимно однозначная функциятакая, что.

Обобщением понятия изоморфизма является понятие гомоморфизма.

Отображение f группоида на группоид называется гомоморфизмом, если.

От гомоморфизма не требуется взаимнооднозначного соответствия, хотя любой изоморфизм называется гомоморфизмом.