Metodichka_po_vyshke_1_ch

21

Если прямая задана общим уравнением Ax + By +C = 0 и при этом B ≠ 0 (т. е. прямая не параллельна оси Oy ), то эта прямая может быть описана урав-

нением с угловым коэффициентом вида y = kx +b .

2. Плоскость и прямая в пространстве. Плоскость P в декартовой пря-

моугольной системе координат Oxyz может быть задана уравнением одного из

n(A, B,C );

3) ax + by + cz =1 – уравнение плоскости в отрезках, где a , b , c – величи-

ны направленных отрезков, отсекаемых плоскостью на координатных осях Ox , Oy и Oz соответственно;

4) xcosα + y cos β + z cosγ − p = 0 – нормальное уравнение плоскости, где cosα , cos β , cosγ – направляющие косинусы нормального вектора n , направленного из начала координат в сторону плоскости, а p > 0 – расстояние от на-

чала координат до плоскости.

Общее уравнение 1) приводится к нормальному виду 4) путём умножения на нормирующий множитель

Если плоскость P задана нормальным уравнением вида 4), а M (x, y, z) – некоторая точка пространства, то выражение

δ (M , P)= xcosα + y cos β + z cosγ − p

задаёт отклонение точки M от плоскости P . Знак δ (M , P) указывает на вза-

имное расположение точки M , плоскости P и начала координат, а именно: если точка M и начало координат лежат по разные стороны от плоскости P , то δ (M , P)> 0 , а если M и начало координат находятся по одну сторону от плос-

кости P , то δ (M , P)< 0.

Расстояние ρ(M , P) от точки M до плоскости P определяется равенст-

вом ρ(M , P)= δ (M , P) .

Прямая L в пространстве может быть задана: 1) общими уравнениями

22

A1x + B1 y +C1z + D1 = 0,A2 x + B2 y +C2 z + D2 = 0,

где коэффициенты A1 , B1 , C1 не пропорциональны коэффициентам A2 , B2 , C2 , что равносильно её заданию как линии пересечения плоскостей;

2)параметрическими уравнениями

x = x0 +lt,y = y0 + mt,z = z0 + nt,

или в векторной форме

r (t ) =r0 +qt ,

где r0 (x0 , y0 , z0 ) – радиус-вектор некоторой точки, принадлежащей прямой, а q(l,m,n) – направляющий вектор прямой;

3) каноническими уравнениями

x −l x0 = y −my0 = z −nz0 ,

что равносильно описанию прямой как линии пересечения трёх плоскостей, проектирующих эту прямую на координатные плоскости.

§ 8. Кривые на плоскости

1. Уравнение кривой в декартовой прямоугольной системе коорди-

нат. Говорят, что кривая Γ в системе координат Oxy имеет уравнение

том и только том случае, когда её координаты удовлетворяют соотношению (3). Если, в частности, F (x, y)= f (x)− y , то уравнение (3) может быть записано в

виде

и в этом случае кривая Γ совпадает с графиком функции f (x).

23

2. Алгебраические кривые второго порядка. Алгебраической кривой второго порядка называется кривая Γ, уравнение которой в декартовой системе координат имеет вид

где не все коэффициенты A , B и C равны одновременно нулю (в противном случае Γ – прямая, т. е. алгебраическая кривая первого порядка).

В общем случае может оказаться, что уравнение (5) определяет так называемую вырожденную кривую (пустое множество, точку, прямую, пару прямых).

Если же кривая Γ невырожденная, то для неё найдётся такая декартова прямоугольная система координат, в которой уравнение этой кривой имеет один из следующих трёх видов (каноническое уравнение):

При этом кривая Γ называется соответственно эллипсом, гиперболой или параболой, а сама система координат, в которой её уравнение имеет вид (6), (7) или (8), называется канонической системой координат для заданной кривой. Рассмотрим основные геометрические свойства невырожденных кривых второго порядка на основе их канонических уравнений.

Параметры a и b называют полуосями эллипса (большой и малой соответственно), точки A1 (−a,0), A2 (a,0), B1 (0,−b) и B2 (0,b) – его вершинами, оси

симметрии Ox и Oy – главными осями, а центр симметрии O – центром эллипса.

Точки F1 (−c,0) и F2 (c,0), где c = a2 −b2 ≥ 0 , называются фокусами эл-

липса, векторы F1M и F2M – фокальными радиус-векторами, а числа r1 = F1M

и r2 = F2M – фокальными радиусами точки M , принадлежащей эллипсу. В частном случае a =b фокусы F1 и F2 совпадают с центром, а каноническое урав-

24

является мерой его «сплюснутости» (при e = 0 эллипс является окружностью). Прямые D1 : x = −a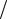e и D2 : x = a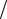e , перпендикулярные главной оси и про-

ходящие на расстоянии a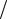e от центра, называются директрисами эллипса. Пусть заданы точки F1 (−c,0) и F2 (c,0), c ≥ 0 . Тогда множество точек M ,

A2 (a,0) – её вершинами, оси симметрии Ox и Oy – действительной и мнимой осями, а центр симметрии O – центром гиперболы.

Прямые y = ± ba x являются асимптотами гиперболы.

болы и является мерой её «сплюснутости». В частном случае a =b гипербола называется равносторонней; её эксцентриситет равен e = 2 , а угол между асимптотами равен π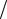2

Прямые D1 : x = −a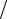e и D2 : x = a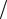e , перпендикулярные действительной

оси и проходящие на расстоянии a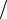e от центра, называются директрисами гиперболы.

Пусть заданы точки F1 (−c,0) и F2 (c,0), c > 0 . Тогда множество точек M ,

где b2 = c2 − a2 .

25

Парабола имеет каноническое уравнение y2 = 2 px, p > 0 .

Число p называется параметром параболы, точка O – её вершиной, а ось Ox – осью параболы.

Точка F (p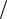2,0) называется фокусом параболы, вектор FM – фокальным радиус-вектором, а число r = FM – фокальным радиусом точки M параболы.

Прямая D : x = − p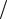2 , перпендикулярная оси и проходящая на расстоянии p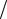2 от вершины параболы, называется её директрисой.

Пусть заданы точка F (p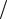2,0) и прямая D : x = − p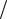2 . Тогда множество

FM

точек M , удовлетворяющих условию ρ(M , D) =1, есть парабола y2 = 2 px .

3. Уравнение кривой в полярной системе координат. Говорят, что на плоскости введена полярная система координат 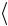O,u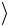 , если заданы:

1)некоторая точка O , называемая полюсом;

2)некоторый луч u , исходящий из точки O и называемый полярной

осью.

Полярными координатами точки M ≠ O называются два числа: полярный радиус r (M )= OM > 0 и полярный угол ϕ(M ) – угол, на который следует по-

вернуть ось u для того, чтобы её направление совпало с направлением вектора OM (при этом, как обычно, ϕ(M )> 0 , если поворот осуществляется против часовой стрелки, и ϕ(M )< 0 в противном случае). Запись M (r,ϕ) означает, что точка M имеет полярные координаты r и ϕ .

Полярный угол ϕ(M ) имеет бесконечно много возможных значений (от-

личающихся друг от друга на величину вида 2πn , n ). Значение полярного угла, удовлетворяющее условию 0 ≤ϕ < 2π , называется главным. В некоторых случаях главным значением полярного угла называют значение ϕ , удовлетворяющее условию −π <ϕ ≤π .

Пусть на плоскости введены правая декартова прямоугольная система координат Oxy (т. е. такая, что кратчайший поворот от оси Ox к оси Oy происхо-

дит против часовой стрелки) и полярная система O,u , причём полярная ось

совпадает с положительной полуосью абсцисс. Тогда связь между декартовыми и полярными координатами произвольной точки M ≠ O даётся формулами

x = r cosϕ, y = r sinϕ;

r = x2 + y2 , tgϕ = yx.

Уравнение кривой в полярных координатах имеет вид F (r,ϕ)= 0 или r = f (ϕ). Оно может быть получено либо непосредственно, исходя из геомет-

26

рических свойств кривой, либо переходом к полярным координатам в уравнении этой кривой, заданном в декартовых прямоугольных координатах.

§ 9. Поверхности и кривые в пространстве

1. Уравнения поверхности и кривой в декартовой прямоугольной

быть записано в виде

z= f (x, y),

ив этом случае поверхность S совпадает с графиком функции двух переменных f (x, y).

Кривая Γ в пространстве в общем случае определяется как линия пересечения некоторых поверхностей S1 и S2 (определяемых неоднозначно), т. е. за-

данием системы двух уравнений

F1 (x, y, z) = 0, F2 (x, y, z) = 0.

2. Алгебраические поверхности второго порядка. Алгебраической по-

верхностью второго порядка называется поверхность S , уравнение которой в декартовой прямоугольной системе координат имеет вид

где не все коэффициенты при членах второго порядка одновременно равны нулю (в противном случае S – алгебраическая поверхность первого порядка, т. е. плоскость).

Может оказаться, что уравнение (10) определяет так называемую вырожденную поверхность (пустое множество, точку, плоскость, пару плоскостей).

Если же поверхность невырожденная, то преобразованием декартовой прямоугольной системы координат её уравнение (10) может быть приведено к одному из указанных ниже видов, называемых каноническими и определяющих тип поверхности.

в) параболический: y2 = 2 px, p > 0 .

Одним из основных методов исследования формы поверхности по её уравнению является метод сечений.

3. Классификация поверхностей по типу преобразований пространст-

ва. Выделяют три класса поверхностей: цилиндрические, конические и поверхности вращения, – инвариантных относительно преобразований соответствующего типа.

Цилиндрической поверхностью (цилиндром) называется поверхность, ин-

вариантная относительно преобразований параллельного переноса, определяемых любым вектором, коллинеарным некоторому вектору q(l,m,n). Из этого

определения следует, что если точка M0 (x0 , y0 , z0 ) принадлежит цилиндру S ,

зующими; всякая кривая Γ, лежащая на цилиндре и пересекающая все его образующие, называется направляющей этого цилиндра.

Пусть q(l,m,n) – любой вектор, коллинеарный оси цилиндра S , а направляющая Γ задана уравнениями

29

чающейся в сечении поверхности любой плоскостью, проходящей через эту ось.

Если, например, поверхность образована вращением кривой F (x, z) = 0 , y = 0 вокруг оси Oz , то уравнение этой поверхности имеет вид

F ( x2 + y2 , z)= 0.

Определители и матрицы. Системы линейных уравнений

§ 10. Определители

1. Определители 2-го и 3-го порядка. Квадратная таблица

A = a11 a12 ,

a21 a22

составленная из четырёх действительных (или комплексных) чисел, называется

квадратной матрицей 2-го порядка. Определителем 2-го порядка, соответст-

вующим матрице A (или просто – определителем матрицы A ), называется

число

– квадратная матрица 3-го порядка, то соответствующим ей определителем 3-го порядка называется число

a11 a12 a13

det A = a21 a22 a23 = a11a22a33 + a12a23a31 + a13a21a32 − a13a22a31 − a12a21a33 − a11a23a32 .(1) a31 a32 a33

Определители 3-го порядка обычно вычисляются с использованием следующего правила Саррюса: одно из трёх слагаемых, входящих в правую часть (1) со знаком плюс, есть произведение элементов главной диагонали матрицыA , каждое из двух других – произведение элементов, лежащих на параллели к этой

30

диагонали, и элемента из противоположного угла матрицы, а слагаемые, вхо-

дящие в (1) со знаком минус, строятся таким же образом, но относительно вто-

рой (побочной) диагонали.

Имеют место следующие свойства определителей 2-го и 3-го порядков:

1)если строки матрицы определителя сделать столбцами с теми же номерами (т. е. транспонировать матрицу), то определитель не изменится;

2)если все элементы строки (столбца) умножить на одно и то же число, то определитель умножится на это число;

3)если переставить две строки (столбца) определителя, то он изменит знак; в частности, если две строки (столбца) определителя равны, то он равен

нулю;

4)если каждый элемент некоторой строки (столбца) определителя представлен в виде суммы двух слагаемых, то определитель равен сумме двух определителей, у которых все строки (столбцы0, кроме данной, прежние, а в данной строке (столбце) в первом определителе стоят первые, а во втором – вторые слагаемые;

5)если одна строка (столбец) является линейной комбинацией остальных строк (столбцов), то определитель равен нулю.

2. Определители n -го порядка. Всякое взаимно-однозначное отображе-

ние π множества первых n натуральных чисел на себя называется подстанов-

кой n -го порядка.

Всякая подстановка может быть записана в виде

рованной подстановки π существует много различных способов записи вида (2), отличающихся нумерацией элементов верхней строки. в частности, запись

вида

называется канонической.

Говорят, что пара элементов (i, j) образует инверсию в подстановке π ,

если i < j , но αi >αj . Число s(π ) всех инверсных пар определяет чётность подстановки: подстановка называется чётной, если s(π ) – чётное число, и нечётной, если s(π ) – число нечётное.

Определителем n -го порядка, соответствующим квадратной матрице