Metodichka_po_vyshke_1_ch

11

– приращение функции y = f (x) в точке x0 , соответствующее приращению ар-

гумента x = x − x0 .

Если в точке x0 нарушено хотя бы одно из условий а) – в), то x0 называется точкой разрыва функции y = f (x). При этом различают следующие слу-

называется точкой разрыва 1-го рода.

в) В остальных случаях точка x0 называется точкой разрыва 2-го рода.

4. Непрерывность на множестве. Равномерная непрерывность. Функ-

ция y = f (x) называется непрерывной на множестве D , если она непрерывна

в каждой точке x D . Она называется равномерно непрерывной на множестве

D , если для любого ε > 0 существует число δ (ε ) > 0 такое, что для любых

§ 5. Комплексные числа

1. Алгебраические операции над комплексными числами. Комплекс-

ными числами называются всевозможные упорядоченные пары z =(x, y) дейст-

вительных чисел, для которых следующим образом определены операции сложения и умножения:

Множество всех комплексных чисел обозначается символом . Действительные числа x и y называются действительной и мнимой

частями комплексного числа z =(x, y) и обозначаются символами Re z и Im z соответственно.

12

Два комплексных числа z1 =(x1, y1 ) и z2 =(x2 , y2 ) называются равными в том и только в том случае, когда x1 = x2 и y1 = y2 .

Из определений (2) и (3) следует, что всякое комплексное число может

Если теперь комплексные числа вида (x,0) отождествить с действительными числами x , а число (0,1) обозначить символом i , то равенство (4) принимает вид

z = x +iy

и называется алгебраической формой комплексного числа z =(x, y).

Если на плоскости введена декартова прямоугольная система координат Oxy , то всякому комплексному числу z = x +iy может быть поставлена в соот-

ветствие некоторая точка M (x, y) с абсциссой x и ординатой y .

При этом говорят, что точка M (x, y) изображает комплексное число z = x +iy . Плоскость, на которой изображаются комплексные числа, называется

комплексной плоскостью, ось Ox – действительной осью, а ось Oy – мнимой

называется аргументом комплексного числа z = x +iy ≠ 0 . Все аргументы числа z различаются на целые кратные 2π и обозначаются единым символом Arg z . Каждое значение аргумента совпадает с величиной ϕ некоторого угла, на кото-

рый следует повернуть ось Ox до совпадения с радиус-вектором OM точки M (при этом ϕ > 0 , если поворот совершается против часовой стрелки, и ϕ < 0 в противном случае). Значение Arg z , удовлетворяющее условию 0 ≤ Arg z < 2π , называется главным значением аргумента и обозначается символом arg z .

Из соотношений (5) следует, что для всякого комплексного числа z справедливо равенство

z = z (cosϕ +isinϕ),

13

называемое тригонометрической формой числа z .

Комплексное число x −iy называется сопряжённым комплексному числу z = x +iy и обозначается символом z .

Пусть ϕ – произвольное действительное число. символом eiϕ обозначается комплексное число cosϕ +isinϕ . с помощью этого обозначения всякое комплексное число z = z (cosϕ +isinϕ) может быть записано в показательной форме

z = z eiϕ .

Справедлива формула Муавра: если z = reiϕ , то

zn = rneinϕ ,

или, в тригонометрической форме,

zn = rn (cos nϕ +isin nϕ).

называются корнями n -й степени из комплексного числа a и обозначаются

символом n a .

2. Предел последовательности комплексных чисел. Число a называют

14

Векторная алгебра и аналитическая геометрия

§ 6. Векторная алгебра

1. Линейные операции над векторами. Вектором (геометрическим вектором) a называется множество всех направленных отрезков, имеющих

одинаковую длину и направление. О всяком отрезке AB из этого множества говорят, что он представляет вектор a (получен приложением вектора a к точке

A ). Длина отрезка AB называется длиной (модулем) вектора a и обозначается символом a = AB . Вектор нулевой длины называется нулевым вектором и

обозначается символом 0.

Векторы a и b называются равными (a =b ), если множества представляющих их направленных отрезков совпадают.

В ряде задач часто бывает удобно не различать вектор и какой-либо представляющий его направленный отрезок. Именно в этом смысле, например, следует понимать выражение «построить вектор».

Пусть направленный отрезок AB представляет вектор a . Приложив к точке B заданный вектор b , получим некоторый направленный отрезок BC .

Вектор, представляемый направленным отрезком AC , называется суммой векторов a и b и обозначается a +b .

Произведением вектора a на действительное число λ называется вектор,

обозначаемый λa , такой, что:

1)λa = λ a ;

2)векторы a и λa сонаправлены при λ > 0 и противоположно направлены при λ < 0 .

Система векторов a1 , …, an называется линейно зависимой, если сущест-

вуют числа λ1 , …, λn такие, что хотя бы одно из них отлично от нуля и λ1a1 +... +λnan = 0 . В противном случае система называется линейно независи-

мой.

Справедливы следующие геометрические критерии линейной зависимо-

сти:

1) система {a1,a2} линейно зависима в том и только в том случае, когда векторы a1 и a2 коллинеарны, т. е. их направления совпадают или противоположны;

2)система {a1,a2 ,a3} линейно зависима в том и только в том случае, когда векторы a1 , a2 и a3 компланарны, т. е. параллельны некоторой плоскости;

3)всякая система из n ≥ 4 векторов линейно зависима.

2. Базис и координаты вектора. Упорядоченная тройка некомпланарных векторов e1 , e2 , e3 называется базисом во множестве всех геометрических век-

торов. Всякий геометрический вектор a может быть единственным образом представлен в виде

15

числа X1 , X2 , X3 называются координатами вектора a в базисе B =(e1,e2 ,e3 ). Запись (1) называют также разложением вектора a по базису B.

Аналогично упорядоченная пара e1 , e2 неколлинеарных векторов называется базисом B =(e1,e2 ) в множестве геометрических векторов, компланарных

некоторой плоскости.

Наконец, всякий ненулевой вектор e образует базис B =(e) в множестве

всех геометрических векторов, коллинеарных некоторому направлению.

Если вектор a есть линейная комбинация векторов a1 , a2 , …, an с коэф-

n

фициентами λ1 , λ2 , …, λn , т. е. a = ∑λkak , то каждая координата Xi (a) векто-

k =1

ра a равна сумме произведений коэффициентов λ1 , …, λn на одноимённые ко-

n

ординаты векторов a1 , …, an : Xi (a)= ∑λk Xi (ak ), i =1,2,3 .

k =1

Базис B =(e1,e2 ,e3 ) называется прямоугольным, если векторы e1 , e2 и e3

попарно перпендикулярны и имеют единичную длину. В этом случае приняты обозначения

e1 = i, e2 = j, e3 =k .

16

называются направляющими косинусами вектора a .

Направляющие косинусы вектора совпадают с координатами (проекциями) его орта a0 = a1 a .

3. Декартовы прямоугольные координаты точки. Простейшие задачи аналитической геометрии. Говорят, что в трёхмерном пространстве введена

декартова прямоугольная система координат, если заданы:

1)некоторая точка O , называемая началом координат;

2)некоторый прямоугольный базис B =(i, j,k ) в множестве всех геомет-

рических векторов.

Оси Ox , Oy и Oz , проведённые через точку O в направлении базисных ортов i , j и k , называются координатными осями системы координат Oxyz .

Если M – произвольная точка пространства, то направленный отрезок

OM называется радиус-вектором точки M . Координатами точки M в систе-

ме Oxyz называются координаты её радиус-вектора OM как геометрического вектора в базисе B, т. е. x(M )= X (OM ), y(M )=Y (OM ), z (M )= Z (OM ).

17

4. Скалярное произведение векторов. Скалярным произведением нену-

левых векторов a1 и a2 называется число

(a1,a2 ) = a1 a2 cos (a1,a2 ).

Для скалярного произведения наряду с обозначением (a1,a2 ) используется также обозначение a1a2 .

Геометрические свойства скалярного произведения:

1)a1 a2 a1a2 = 0 (условие перпендикулярности векторов);

2)если ϕ = (a1,a2 ), то

0 ≤ϕ <π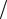2 a1a2 > 0

и

π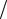2 <ϕ ≤π a1a2 < 0.

Из этой формулы, в частности, следует формула для определения косинуса угла между векторами

Если задан некоторый вектор e , то ортогональной составляющей произвольного вектора a вдоль вектора e называется такой вектор ae , который кол-

линеарен e , причём разность a −ae перпендикулярна вектору e .

Аналогично ортогональной составляющей вектора a в плоскости P на-

зывается вектор aP , компланарный плоскости P , причём разность a −aP перпендикулярна этой плоскости.

18

Если базис B =(e1,e2 ,e3 ) – прямоугольный, то координаты произвольного вектора a = X1e1 + X2e2 + X3e3 в этом базисе могут быть вычислены по формуле

Xi =aei , i =1,2,3.

5. Векторное произведение векторов. Упорядоченная тройка некомпла-

нарных векторов e1 , e2 , e3 называется правой, если наблюдателю, находящему-

ся внутри телесного угла, образованного этими векторами, кратчайшие повороты от e1 к e2 и от e2 к e3 кажутся происходящими против часовой стрелки. в

противном случае тройка e1 , e2 , e3 называется левой.

Векторным произведением вектора a1 на вектор a2 называется вектор, обозначаемый символом [a1,a2 ] (или a1 ×a2 ), определяемый следующими тре-

мя условиями:

1) длина вектора [a1,a2 ] равна площади параллелограмма, построенного на векторах a1 и a2 , т. е. [a1,a2 ] = a1 a2 sin (a1,a2 );

2)вектор [a1,a2 ] перпендикулярен плоскости векторов a1 и a2 ;

3)упорядоченная тройка a1 , a2 , [a1,a2 ] правая.

Из определения векторного произведения следует, что

a1 a2 [a1,a2 ]= 0 .

Алгебраические свойства векторного произведения: 1) [a1,a2 ]= −[a2 ,a1 ];

2) [λa1,a2 ]= λ[a1,a2 ];

3) [a1 +a2 ,b]=[a1,b]+[a2 ,b].

Если a1 (X1,Y1, Z1 ) и a2 (X2 ,Y2 , Z2 ) – векторы, заданные своими координатами в правом прямоугольном базисе, то разложение векторного произведения в том же базисе имеет вид

[a1,a2 ]=(Y1Z2 − Z1Y2 )i +(Z1 X2 − X1Z2 )j +(X1Y2 −Y1 X2 )k ,

или, в символической записи с использованием понятия определителя 3-го порядка

19

6. Смешанное произведение векторов. Смешанным произведением упо-

рядоченной тройки векторов a1 , a2 , a3 называется число [a1,a2 ]a3 .

Геометрические свойства смешанного произведения:

1) если V – объём параллелепипеда, построенного на векторах a1 , a2 и

a3 , то

V , если тройка (a ,a ,a ) правая,

[a ,a ]a = 1 2 3

1 2 3 −V , если тройка (a1,a2 ,a3 ) левая;

2)для того, чтобы три вектора a1 , a2 , a3 были компланарны, необходимо

идостаточно выполнение условия [a1,a2 ]a3 = 0 .

Основное алгебраическое свойство смешанного произведения состоит в том, что циклическая перестановка векторов не меняет его величины, т. е.

[a1,a2 ]a3 =[a2 ,a3 ]a1 =[a3 ,a1 ]a2 .

Это свойство позволяет ввести обозначение [a1,a2 ]a3 =a1a2a3 (результат не за-

висит от того, как расставить квадратные скобки в правой части). Смешанное произведение через координаты векторов в правом прямоугольном базисе записывается в виде

X1 Y1 Z1

a1a2a3 = X2 Y2 Z2 .

X3 Y3 Z3

§ 7. Линейные геометрические объекты

1. Прямая на плоскости. Прямая на плоскости в декартовой прямоугольной системе координат Oxy может быть задана уравнением одного из

следующих видов:

1)Ax + By +C = 0 – общее уравнение прямой;

2)A(x − x0 )+ B(y − y0 )= 0 – уравнение прямой, проходящей через точку

M0 (x0 , y0 ) перпендикулярно нормальному вектору n(A, B);

ние прямой);

рые в векторной форме имеют вид

r =r0 +qt ,

где r0 (x0 , y0 ) – радиус-вектор точки M0 (x0 , y0 ), q(l,m) – направляющий вектор прямой;

5) ax + by =1 – уравнение прямой в отрезках, где a и b – величины на-

правленных отрезков, отсекаемых прямой на координатных осях Ox и Oy со-

ответственно;

6) xcosα + y cos β − p = 0 – нормальное уравнение прямой, где cosα и cos β – направляющие косинусы нормального вектора n , направленного из начала координат в сторону прямой, а p > 0 – расстояние от начала координат до

прямой.

Общее уравнение 1) приводится к нормальному виду 6) путём умножения на нормирующий множитель

μ = − sgn C .

A2 + B2

Если прямая L задана уравнением вида 6), а M (x, y) – некоторая точка плоскости, то выражение

δ (M , L)= xcosα + y cos β − p

задаёт отклонение точки M от прямой L . Знак δ (M , L) указывает на взаим-

ное расположение точки M , прямой L и начала координат, а именно: если точка M и начало координат лежат по разные стороны от прямой L , то δ (M , L)> 0 , а если M и начало координат находятся по одну сторону от пря-

мой L , то δ (M , L)< 0 . Расстояние ρ(M , L) от точки M до прямой L определяется равенством ρ(M , L)= δ (M , L) .

Пусть заданы две прямые L1 и L2 . Возможны два случая их взаимного расположения:

1)L1 и L2 – параллельные прямые, в частности они совпадают;

2)L1 и L2 пересекаются.