Решение

В пункте 1) условия явно указано, что A,BиCявляются исходными работами, поэтому изобразим их тремя стрелками, выходящими из исходного события 1. Пункт 2) условия означает, что стрелки работAиBдолжны окончиться в одном событии, из которого выйдет стрелка работыD. Но поскольку стрелки работAиBтакже и начинаются в одном событии, то имеет место параллельность работ, которая недопустима правилами построения сетевых моделей (см. рис.4).

Рис.4. Устранение параллельности работ AиB

Для ее устранения введем дополнительное событие 2, в которое войдет работа B, после чего соединим события 2 и 3, в которые входят работыAиBпунктирной стрелкой фиктивной работы. В данном случае фиктивная работа (2,3) не соответствует никакой реальной работе, а лишь отображает логическую связь между работамиBиD. Дальнейшее построение рассмотрим с помощью рис.5

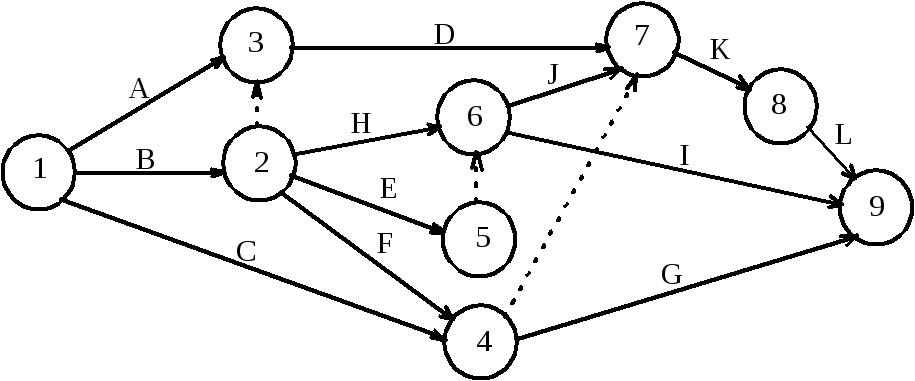
Рис.5. Сетевая модель задачи №7.02

Согласно пункту 3) условия задачи из события 2, выходят три стрелки работE,FиH. Согласно пункту 4) условия задачи стрелки работCиFдолжны войти в общее событие, из которого выйдет стрелка работыG. Проблема с параллельностью работEиH[пункт 5) условия задачи] решается путем введения дополнительного события 5 и фиктивной работы (5,6). Для отображения в сетевой модели пункта 6) условия задачи введем стрелки работDиJв событие 7, а связь работFиCс работойKотобразим с помощью фиктивной работы (4,7). Стрелки работFиCнельзя было напрямую вводить в событие 7, потому что после них должна следовать работаG, которая с работамиDиJникак не связана. Стрелка работыLвыходит из события 8, т.е. после окончания работыKв соответствии с пунктом 7) условия задачи.

Поскольку в условии не указано, что работы L,IиGпредшествуют каким-либо другим работам, то эти работы являются завершающими и их стрелки войдут в завершающее событие 9. Нумерацию событий проводят после построения сетевого графика, следя за тем, чтобы номер начального события каждой работы был меньше номера ее конечного события.

Расчет сетевых моделей

Календарное планирование предусматривает определение моментов начала и окончания каждой работы и других временных характеристик сетевого графика. Это позволяет проанализировать сетевую модель, выявить критические работы, непосредственно определяющие срок выполнения проекта, провести оптимизацию использования ресурсов (временных, финансовых, исполнителей).

Расчет сетевой модели начинают с временных параметров событий, которые вписывают непосредственно в вершины сетевого графика (рис.8.1):

• – ранний срок наступления событияi, минимально необходимый для выполнения всех работ, которые предшествуют событиюi;

• – поздний срок наступления событияi, превышение которого вызовет аналогичную задержку наступления завершающего события сети;

• – резерв событияi, т.е. время, на которое может быть отсрочено наступление событияiбез нарушения сроков завершения проекта в целом.

Рис.6. Отображение временных параметров событий на сетевом графике

Ранние сроки свершения событий рассчитываются от исходного (И) к завершающему (З) событию следующим образом:

1. для исходного события И ;

2. для всех остальных событий I

,

где максимум берется по всем работам , входящим в событие i;– длительность работы (k,i) (рис.8.2).

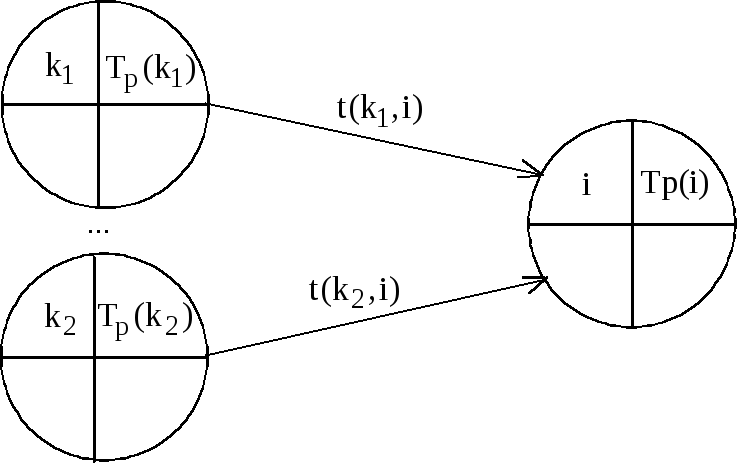
Рис.7 Расчет раннего срока свершения событияi

Поздние сроки свершения событий рассчитываются от завершающего к исходному событию:

1. для завершающего события З ;

2. для всех остальных событий

,

где минимум берется по всем работам , выходящим из события i;– длительность работы (k,i) (рис.8.3).

Рис.8 Расчет позднего срока свершения событияi

Временные параметры работ определяются на основе ранних и поздних сроков событий:

• – ранний срок начала работы;

• – ранний срок окончания работы;

• – поздний срок окончания работы;

• – поздний срок начала работы;

• – полный резерв работы показывает максимальное время, на которое можно увеличить длительность работыили отсрочить ее начало, чтобы не нарушился срок завершения проекта в целом;

• – свободный резерв работы показывает максимальное время, на которое можно увеличить продолжительность работыили отсрочить ее начало, не меняя ранних сроков начала последующих работ.

Путь –это последовательность работ в сетевом графике (в частном случае это одна работа), в которой конечное событие одной работы совпадает с начальным событием следующей за ней работы.

Полный путь –это путь от исходного до завершающего события.

Критический путь –максимальный по продолжительности полный путь. Работы, лежащие на критическом пути, называюткритическими. Критические работы имеют нулевые свободные и полные резервы.

Подкритический путь –полный путь, ближайший по длительности к критическому пути.

Для проведения анализа временных параметров сетевой модели используютграфик привязки, который отображает взаимосвязь выполняемых работ во времени. По вертикальной оси графика привязки откладываются коды работ, по горизонтальной оси – отрезки, соответствующие длительностям работ (раннее начало и раннее окончание работ). График привязки можно построить на основе данных о продолжительности работ. При этом необходимо помнить, что работаможет выполняться только после того как будут выполнены все предшествующие ей работы.

Пример расчета сетевой модели

Рис.9. Расчет сетевой модели

Оптимизация комплекса работ по времени

Оптимизация комплекса операций по времени сводится к сокращению продолжительности критического пути. Необходимость проведения оптимизации сетевого графика по времени возникает тогда, когда критическое время выполнения комплекса операций превосходит срок T₀, на котором настаивает ЛПР. Очевидно, подобная задача требует проведения определенных мероприятий и (или) вложения дополнительных средств.

Иногда оптимизация достигается за счет перепланировки сетевого проекта (изменения топологии сети). Например, одновременно выполняемые операции, имеющие резервы времени и не лежащие на критическом пути, могут выполняться последовательно (если это допускается технологией). Освободившиеся при этом ресурсы можно использовать на критических операциях, что ускорит их выполнение. Сокращение времени выполнения операций возможно также за счет автоматизации производственных процессов, улучшения организации работ, использования передовых технологий и т.д.

Оптимизация комплекса операций по времени может проводиться с привлечением дополнительных средств и с использованием внутренних резервов.

Приведем математическую формулировку процесса оптимизации по времени.

Пусть задан сетевой график выполнения комплекса операций. Время выполнения каждой операции равно t_ij. Пусть также вложение дополнительных средств в операцию сокращает время выполнения сt_ijдоt^’_ij. Естественно, для каждой операции существует минимально возможное время ее выполнения, равноеd_ij. Требуется определить время начала и окончания выполнения операций, а также величину дополнительных средствx_ij, которые необходимо вложить в каждую из операций(i, j), чтобы общее время выполнения комплекса операций было минимальным. При этом сумма вложенных дополнительных средств не должна превышать заданной величиныc, а время выполнения каждой операции должно быть не меньше минимально возможного времениd_ij.

Математически условия задачи можно записать следующим образом:

Ограничение (2) определяет сумму вложенных дополнительных средств: она не должна превышать величины c. Ограничения (3) показывают, что продолжительность каждой работы должна быть не менее минимально возможной ее продолжительности. Ограничения-равенства (4) показывают зависимость продолжительности каждой работы от вложенных в нее дополнительных средств. Ограничения (5) обеспечивают выполнение условий предшествования работ в соответствии с топологией сети: время начала выполнения каждой работы должно быть не меньше времени окончания непосредственно предшествующих ей работ, (6) — условие неотрицательности.

Если в последнее событие сети п входят сразу несколько работ, то необходимо добавить фиктивную работу (n, n+1), время выполнения которой равно нулю (t^o_n,n+1-t^н_n,n+1=0 добавить в ограничение (4)). Тогда целевая функция запишется так

t_кр=t^o_n,n+1 → (min)

Приведенные постановки задачи относятся к классу задач математического программирования и могут быть решены известными методами в зависимости от вида функций f_ij (х_ij). Если предположить, что продолжительность выполнения работ линейно зависит от дополнительно вложенных средств и выражается соотношением

где k_ij — технологические коэффициенты использования дополнительных средств, то будем иметь задачу линейного программирования.

Пример.

Для сокращения срока реализации проекта, представленного сетевым графиком (рис.10), заказчик выделил 14 ед. дополнительных средств. Продолжительность выполнения работ линейно зависит от дополнительно вложенных средств и выражается соотношением t'_ij = t_ij - k_ij x_ij. Известно, что k_l2=0,1; k₁₃ = 0,2; k₂₃ = 0,5; k₂₄ = 0,3; k₃₅ = 0,6; k₄₅ = 0,1. Над каждой работой поставлена ее продолжительность t_ij и минимально возможное время выполнения d_ij.

Рис. 10

Требуется оптимизировать сетевой график по времени, то есть найти такие , , x_ij чтобы:

а) время выполнения всего проекта было минимальным;

б) сумма дополнительно вложенных средств не превышала 14 ед.;

Ниже приводится образец решения задачи в Excel

Таким образом, при дополнительном вложении 14 ед. комплекс работ может быть выполнен за 30 ед. времени. При этом средства распределятся следующим образом: 4 ед. в работу (2, 3) и 10 ед. в работу (3, 5) (Рис.4).

Постановка задачи 2. Пусть задан срок выполнения проекта t_o, а расчетное t_кр > t_o. В этом случае оптимизация комплекса работ сводится к сокращению продолжительности критического пути. Задача заключается в определении величины дополнительных вложений x_ij в отдельные работы проекта, с тем чтобы общий срок его выполнения не превышал заданной величины t_o, а суммарный расход дополнительных средств был минимальным. Время выполнения каждой работы должно быть не меньше минимально возможного времени d_ij.

Математическая запись этой задачи:

Смысл ограничений аналогичен соответствующим ограничениям постановки задачи 1 (1) — (6).

Приведенные постановки задачи относятся к классу задач математического программирования и могут быть решены известными методами в зависимости от вида функций f_ij (х_ij). Если предположить, что продолжительность выполнения работ линейно зависит от дополнительно вложенных средств и выражается соотношением

где k_ij — технологические коэффициенты использования дополнительных средств, то будем иметь задачу линейного программирования.

Оптимизация проекта по стоимости

В общем случае стоимость выполнения работы зависит от ее продолжительности. Продолжительность каждой работы может изменяться между двумя границами d_ij и D_ij, определяемыми техническими или экономическими соображениями. Если D_ij — нормальная продолжительность, ей соответствует минимальная стоимость c_ij выполнения работы (i, j); если d_ij — минимально возможная (экстренная) продолжительность работы, при этом стоимость работы будет максимальной С_ij;. Если при планировании проекта для каждой работы будет взята ее нормальная (наибольшая) длительность D_ij, то стоимость проекта будет минимальной. Если для каждой работы взять ее ускоренную, минимально возможную продолжительность d_ij, мы получим срочный план. Стоимость выполнения проекта в этом случае будет максимальной.

Зависимость стоимости от продолжительности работы нелинейна, но для упрощения оптимизационных расчетов предполагают, что уменьшение продолжительности работы пропорционально возрастанию ее стоимости. Тогда в расчете на единицу времени дополнительные затраты на сокращение продолжительности работы будут равны

Рассмотрим оптимизацию комплекса работ по стоимости при фиксированном сроке выполнения.

Предполагается, что все работы выполняются в срочном режиме и исходная стоимость проекта

максимальна. Необходимо минимизировать стоимость проекта при фиксированном сроке его завершения t_o за счет увеличения времени выполнения отдельных работ.

Увеличение продолжительности работы (i,j) по сравнению с минимальным сроком выполнения на (t°_ij - t^н_ij - d_ij) вызовет экономию средств на величину h_ij (t°_ij -t^н_ij - d_ij), a стоимость выполнения работы станет равна

С = C_ij - h_ij (t^o_ij - t^н_ij - d_ij).

Если t_o = t_кр, то оптимизация осуществляется за счет увеличения продолжительности некритических работ; если t_кр < t_о, — то за счет всех работ комплекса.

Математическая записьзадачи:

Здесь 1 — номер исходного события, п — номер завершающего события.

Рассмотрим оптимизацию комплекса работ по стоимости при нефиксированном сроке выполнения.

Пусть задан сетевой график проекта и известны продолжительность каждой работы и стоимость ее выполнения в нормальном (D_ij, c_ij) и срочном (d_ij;, C_ij) режиме работы. Если все работы выполняются в нормальном режиме, то критический срок будет наибольшим, а стоимость выполнения — наименьшей. Время выполнения проекта может быть уменьшено путем увеличения стоимости. Необходимо сократить критический срок до некоторого минимально возможного значения при наименьшем возрастании стоимости выполнения проекта.

Динамическое программирование

Предмет динамического программирования

Динамическое программирование (иначе, «динамическое планиро­вание») представляет собой особый математический метод оптимизации решений, специально приспособленный к многошаговым (или многоэтапным) операциям.

Представим себе, что исследуемая операция Qпредставляет собой процесс, развивающийся во времени и распадающийся на ряд «шагов» или «этапов». Некоторые операции расчленяются на шаги естественно: например, при планировании хозяйственной деятельности группы предприятий естественным шагом является хозяйственный год. В дру­гих операциях разделение на шаги приходится вводить искусственно.

Процесс, о котором идет речь, является управляемым, т.е. на каждом шаге принимается какое-то решение, от которого зави­сит успех данного шага и операции в целом. Управление операцией складывается из ряда элементарных, «шаговых» управлений.

Рассмотрим пример естественно-многошаговой операции Q. Пусть планируется деятельность группы (системы) промышленных предприя­тий П₁П₂, П_кна некоторый период времени T состоящий изmхозяйственных лет (рис. 1).

В начале периода на развитие системы предприятий выделяются какие-то основные средства K₀, которые должны быть как-то распреде­лены между предприятиями. В процессе функционирования системы выделенные средства частично расходуются (амортизируются). Кроме того, каждое предприятие за год приносит некоторый доход, зависящий от вложенных средств. В начале каждого хозяйственного года имею­щиеся средства могут перераспределяться между предприятиями: каждому из них выделяется какая-то доля средств.

Ставится вопрос: как нужно в начале каждого года распределять имеющиеся средства между предприятиями, чтобы суммарный доход от всей системы предприятий за весь период Т = m был максимальным?

Перед нами — типичная задача динамического про г р а м м и р о в а н и я.

Рассматривается управляемый процесс — функционирование системы предприятий. Управление процессом состоит в распреде­лении (и перераспределении) средств. Шагом управления является выделение каких-то средств каждому из предприятий в начале хозяй­ственного года,

Пусть в начале 1-го года предприятиям П₁П₂, П_kвыделяются соответственно средства:

Совокупность этих значений представляет собой не что иное, как управление на i-м шаге:

U_i=(X_i⁽¹⁾, X_i⁽²⁾, … ,X_i^(k)).

Управление может быть хорошим или плохим, эффективным или неэффективным. Эффективность управления U оценивается тем же показателем W, что и эффективность операции в целом. В нашем при­мере показатель эффективности (целевая функция) представляет собой суммарный доход от всей системы предприятий за mлет. Он зависит от управления операцией U, т. е. от всей совокупности шаговых управ­лений: УправлениеU операцией в целом представляет собой совокупность всех шаговых управлений:

Возникает вопрос: как выбрать шаговые управления U₁,U₂, …, Um для того, чтобы величина W обратилась в максимум?

Поставленная задача называется задачей оптимизации управления, а управление, при котором показатель W дости­гает максимума, — оптимальным управлением. Будем обозначать оптимальное управление (в отличие от управления вообще U) буквой u. Оптимальное управление многошаговым процессом состоит из совокупности оптимальных шаговых управлений:

Таким образом, перед нами стоит задача: определить оптимальное управление на каждом шаге u_i(i=1, 2, …,m) и, значит, оптимальное управление всей операциейu.

Заметим, что в нашем примере (управление финансированием си­стемы предприятий) показатель эффективности W представляет собой сумму доходов за все отдельные годы (шаги):

где w_i— доход от всей системы предприятий заi-й год.

Поставим задачу динамического программирования в общем виде. Пусть имеется операцияQс показателем эффективности (1), распадающаяся (естественно или искусственно) наmшагов. На каждом шаге применяется какое-то управление U_i. Требуется найти оптимальное управление

при котором показатель эффективности

обращается в максимум.

Поставленную задачу можно решать по-разному: или искать сразу оптимальное управление и, или же строить его постепенно, шаг за ша­гом, на каждом этапе расчета оптимизируя только один шаг. Обычно второй способ оптимизации оказы­вается проще, чем первый, особенно при большом числе шагов.

Такая идея постепенной, пошаговой оптимизации процесса и со­ставляет суть метода динамического программирования.

При использовании метода динамического программирования следует учитывать то, что шаговое управление должно выбираться с учетом всех его последствий в будущем. Планирование должно быть дальновидным, с учетом перспективы, иначе возможны серьезные ошибки.

Например, пусть планируется работа группы промыш­ленных предприятий, одни из которых заняты выпуском предметов по­требления, другие же производят для этого машины. Задачей является получение за mлет максимального объема выпуска предметов потреб­ления. Пусть планируются капиталовложения на первый год. Исходя из узких интересов данного шага (года), мы должны были бы все сред­ства вложить в производство предметов потребления, пустить имею­щиеся машины на полную мощность и добиться к концу года макси­мального объема продукции. Но правильным ли будет такое решение с точки зрения операции в целом? Очевидно, нет. Имея в виду будущее, необходимо выделить какую-то долю средств и на производство машин. При этом объем продукции за первый год, естественно, снизится, зато будут созданы условия, позволяющие увеличивать ее производство в последующие годы.

Таким образом, планируя многошаговую операцию, необходимо вы­бирать управление на каждом шаге с учетом его будущих последствий на еще предстоящих шагах.

Однако из этого правила есть исключение. Среди всех шагов су­ществует один, который может планироваться без «оглядки на будущее». Очевидно, это последний — после не­го других шагов нет. Этот шаг, единственный из всех, можно плани­ровать так, чтобы он как таковой принес наибольшую выгоду. Сплани­ровав оптимально этот последний шаг, можно к нему пристраивать предпоследний, к предпоследнему — пред-предпоследний и т. д.

Поэтому процесс динамического программирования разворачи­вается от конца к началу: раньше всех планируется послед­ний, m-й шаг. А как его спланировать, если мы не знаем, чем кончил­ся предпоследний? Очевидно, нужно сделать разные предположения о том, чем кончился пред­последний (m-1)-й ш а г, и для каждого из них найти такое управление, при котором выигрыш (доход) на последнем шаге был бы максимален. Решив эту задачу, мы найдем условное опти­мальное управление на m-м шаге, т. е. то управление, кото­рое надо применить, если (m-1)-й шаг закончился определенным образом.

Предположим, что эта процедура выполнена, и для каждого исхода (m-1)-го шага мы знаем условное оптимальное управление наm-м шаге и соответствующий ему условный оптимальный выигрыш. Теперь мы можем оптимизировать управление на предпоследнем, (m-1)-м шаге. Сделаем все возможные предположения о том, чем кончился пред-предпоследний, (m-2)-й шаг, и для каждого из этих предполо­жений найдем такое управление на (m-1)-м шаге, чтобы выигрыш за последние два шага (из которых последний уже оптимизирован) был максимален. Далее оптимизируется управление на (m-2)-м шаге, и т. д.

Одним словом, на каждом шаге ищется такое управление, которое обеспечивает оптимальное продолжение процесса относительно достигнутого в данный момент состояния. Этот прин­цип выбора управления называется принципом оптималь­ности. Само управление, обеспечивающее оптимальное продолже­ние процесса относительно заданного состояния, называется услов­ным оптимальным управлением на данном шаге.

Теперь предположим, что условное оптимальное управление на каждом шаге нам известно: мы знаем, что делать дальше, в каком бы состоянии ни был процесс к началу каждого шага. Тогда мы можем найти уже не «условное», а просто оптимальное управление на каждом шаге.

Действительно, пусть нам известно начальное состояние процесса, обозначим его S₀. Теперь мы уже знаем, что делать на первом шаге: надо применить условное оптимальное управление, выработанное на­ми для первого шага, относящееся к состоянию S₀. В результате этого управления после первого шага система перейдет в другое состояние, но для этого состояния мы снова знаем условное оптимальное уп­равление на втором шагеu₂, и т. д. Таким образом мы найдем оптималь­ное управление процессом

приводящее к максимально возможному выигрышу W_max,

Таким образом, в процессе оптимизации управления методом ди­намического программирования многошаговой процесс «проходится» дважды:

первый раз — от конца к началу, в результате чего находятся условные оптимальные управления на каждом шаге и оптимальный выигрыш (тоже условный) на всех шагах, начиная с данного и до конца процесса;

второй раз — от начала к концу, в результате чего находятся (уже не условные) оптимальные шаговые управления на всех шагах операции.

Задачи нахождения кратчайшего пути на сети дорог (задача о рациональном маршруте доставки)

На данной сети дорог указаны стоимости доставки единицы груза из пункта в пункт. Найти наиболее экономный маршрут перевозки груза из пункта 1 в пункт 10.

2

3

1

3

4

5

7

6

3

2

3

8

10

3

2

4

2-й шаг

1-й шаг

4-й шаг

3-й шаг

Решение. Минимизировать затраты по доставке целесообразно применительно к единице груза, ибо понятно, что если затраты минимальны при перевозке единицы груза, то они будут минимальными и при перевозке любого количества груза.

Концепция динамического программирования предполагает, что процессу принятия решения в оптимизационной задаче может быть придан шаговый характер. С этой целью разобьем все пункты сети на группы.

К группе I отнесем пункт 1, к группе II — пункты, в которые можно попасть непосредственно из пункта 1 (таковыми будут 2 и 3), к группе III отнесем пункты, в которые можно попасть непосредственно из любого пункта группы II (таковыми будут 4, 5 и 6), и т. д. В результате движение транспорта с грузом из пункта 1 в пункт 10 можно рассматривать как четырехшаговый процесс: на первом шаге транспорт перемещается из пункта 1 в какой-то пункт группы II, на втором шаге — из пункта группы II в пункт группы III и т. д

I	II	III	IV	V
	2	4	7
1	3	5	8	10
		6	9

1-й шаг:

	Конечный пункт	Общие минимальные затраты f1(S)	Конечный пункт на оптимальном маршруте j1(S)
Начальный пункт S	10
7	3	3	10
8	2	2	10
9	4	4	10

2-й шаг:

	Конечный пункт			Общие минимальные затраты f2(S)	Конечный пункт на оптимальном маршруте j2(S)
Начальный пункт S	7	8	9
4	5+3	7+2	-	8	7
5	6+3	10+2	8+4	9	7
6	-	3+2	-	5	8

3-й шаг:

	Конечный пункт			Общие минимальные затраты f3(S)	Конечный пункт на оптимальном маршруте j3(S)
Начальный пункт S	4	5	6
2	1+8	3+9	-	9	4
3	4+8	3+9	2+5	7	6

4-й шаг

	Конечный пункт		Общие минимальные затраты f4(S)	Конечный пункт на оптимальном маршруте j4(S)
Начальный пункт S	2	3
1	2+9	3+7	10	3

Выписываем оптимальный маршрут (начиная с последней таблицы): 1-3-6-8-10, при этом общие минимальные затраты составят 10ед.

Аналогично можно выписать оптимальные пути из любого пункта.

Определение оптимального срока замены транспортного средства

Транспортные расходы, в том числе расходы на содержание транспортных средств, в структуре затрат на логистику занимают свыше 40%. Сократить эту статью расходов позволит своевременная замена транспортного средства. Решение данной задачи основано на понимании того, что всякое транспортное средство (автомобиль, погрузчик и т. д.), несмотря на массовый характер сборки, "болеет по-своему", т. е. в процессе эксплуатации имеет индивидуальную динамику расходов на ремонт. Система учета затрат, направленных на поддержание работоспособности транспортного парка, должна обеспечивать выявление "слабой" техники, замену которой необходимо осуществлять в первую очередь.

Как свидетельствует практика, данная задача ставится и решается прежде всего на предприятиях, имеющих в своем составе службу логистики.

Методика определения срока (точки) замены транспортного средства, основана на точном учете затрат на ремонт в процессе эксплуатации транспортного средства, а также на маркетинговых исследованиях рынка транспортных средств, бывших в употреблении.

Задача

Автомобиль, купленный за 40 000 у.е., эксплуатировался 6 лет, ежегодно проезжая по 20 тыс., км. Годовые затраты на ремонт приведены в гр. 3 табл. 1. В ней же указана рыночная стоимость автомобиля к концу каждого года эксплуатации (гр. 4). Определить срок замены транспортного средства методом минимума общих затрат.

Решение

Для определения точки (срока) замены необходимо определить две следующие зависимости:

1) f1(х) — зависимость расходов на ремонт, приходящихся на единицу выполненной автомобилем работы, от количества выполненной работы;

2) f2(x) — зависимость расхода капитала, приходящегося на единицу выполненной работы, от количества выполненной работы.

Найденные зависимости f1(х) и f2(х) позволят определить функцию F(x) — зависимость суммарных затрат, т.е. расходов на ремонт и расхода капитала, от величины пробега. Минимальное значение функции F(x) и укажет срок замены транспортного средства.