
- •1 Предмет изучения дисциплины
- •2 Содержание экономико-математических моделей и методика их построения
- •3 Общая классификация экономико-математических моделей
- •4 ЛинейныЕ экономико-математическиЕ моделИ
- •Матричные игры
- •Платежная матрица
- •Нижняя и верхняя цена игры
- •Смешанные стратегии
- •Решение матричной игры графическим методом
- •Решение игр с природой по различным критериям
- •Решение
- •Исходные данные для расчета точки минимума общих затрат (начальная стоимость автомобиля – 40000 у. Е.)
Нижняя и верхняя цена игры
|
|
|
|
… |
|
|
|
|
|
|
… |
|
|
|
|
|
|
… |
|
|
|
|
… |
… |
… |
… |
… |
|
|
|
|
… |
|
|
|
|
|
|
… |
|
|
В таблице приведены числа
![]() -
минимально возможный выигрыш игрока
А, применяющего стратегию
-
минимально возможный выигрыш игрока
А, применяющего стратегию![]() (
(![]() )
и
)
и![]() - максимально возможный проигрыш игрока
В, если он пользуется стратегией
- максимально возможный проигрыш игрока
В, если он пользуется стратегией![]() (
(![]() ).
).
Число
![]() называютнижней чистойценой игры(максимином), а соответствующую ему
чистую стратегию – максиминной.
называютнижней чистойценой игры(максимином), а соответствующую ему
чистую стратегию – максиминной.
Число
![]() показывает, какой минимальный
гарантированный выигрыш может получить
игрок А, правильно применяя свои чистые
стратегии при любых действиях игрока
В.
показывает, какой минимальный
гарантированный выигрыш может получить
игрок А, правильно применяя свои чистые
стратегии при любых действиях игрока
В.
Число
![]() называютверхней чистой ценой игры(минимаксом), а соответствующую чистую
стратегию минимаксной.
называютверхней чистой ценой игры(минимаксом), а соответствующую чистую
стратегию минимаксной.
Число
![]() показывает, какой минимальный
гарантированный проигрыш может быть у
игрока В, при правильном выборе им своих
чистых стратегий независимо от действий
игрока А.
показывает, какой минимальный
гарантированный проигрыш может быть у
игрока В, при правильном выборе им своих
чистых стратегий независимо от действий
игрока А.
Ясно, что
![]() .
.
Если
![]() ,
то говорят, что игра имеет седловую
точку в чистых стратегиях и чистую цену
игры
,
то говорят, что игра имеет седловую
точку в чистых стратегиях и чистую цену
игры![]() .
Стратегии образующие седловую точку,
являются оптимальными. Тройку (
.
Стратегии образующие седловую точку,
являются оптимальными. Тройку (![]() )
называют решением игры.
)
называют решением игры.
Пример
Проверим наличие седловой точки.
-
1
4
9
16
1
16
9
4
1
1
10
10
10
15
10
16
10
10
16
Для игрока А: Max (1, 1, 10) = 10
Для игрока В: min(16, 10, 10, 16) = 10
Седловые точки - (3, 2) и (3, 4). Цена игры = 10; оптимальный выбор для игрока 1 - третий, для игрока 2 равнозначны второй и третий
Смешанные стратегии
Для игр без седловых точек оптимальные стратегии игроков находятся в области смешанных стратегий.
Смешанной стратегией игрока А называют
вектор
![]() ,
компоненты которого удовлетворяют
условиям
,
компоненты которого удовлетворяют
условиям![]() .
.
Смешанной стратегией игрока В называют
вектор
![]() ,
компоненты которого удовлетворяют
условиям
,
компоненты которого удовлетворяют
условиям![]() .
.
![]() и
и![]() - вероятности, с которыми игроки А и В
выбирают свои чистые стратегии
- вероятности, с которыми игроки А и В
выбирают свои чистые стратегии![]() и
и![]() в ходе игры.
в ходе игры.
При использовании смешанных стратегий
игра приобретает случайный характер,
случайной становится и величина выигрыша
игрока А (проигрыша игрока В). Эта величина
является функцией смешанных стратегий
![]() и
и![]() и определяется по формуле
и определяется по формуле![]() .
.
Функцию
![]() называют функцией выигрыша или платежной
функцией.
называют функцией выигрыша или платежной
функцией.
Смешанные стратегии называются
оптимальными, если они образуют седловую
точку для платежной функции
![]() ,
т.е. если они удовлетворяют неравенству
,
т.е. если они удовлетворяют неравенству![]() .
.
Величину
![]() называют ценой игры.
называют ценой игры.
Поиск оптимальных смешанных стратегий
начинают с упрощения платежной матрицы.
Если в платежной матрице элементы k-й
строки не меньше соответствующих
элементовs-й строки, т. е.![]() ,
то говорят, что стратегия
,
то говорят, что стратегия![]() доминирует над стратегией
доминирует над стратегией![]() .
Аналогично, если элементыl-го
столбца не превосходят соответствующих
элементовr-го столбца, т. е.
.
Аналогично, если элементыl-го
столбца не превосходят соответствующих
элементовr-го столбца, т. е.![]() ,
то говорят, что стратегия
,
то говорят, что стратегия![]() доминирует над стратегией
доминирует над стратегией![]() .
Частным случаем доминирования стратегий
является дублирование стратегий, когда
.
Частным случаем доминирования стратегий
является дублирование стратегий, когда![]() или
или![]() .
Исключение из платежной матрицы
доминируемых стратегий (ими игрокам
пользоваться заведомо невыгодно)
позволяет уменьшить ее размерность, а
это упрощает решение игры. Вероятность
применения доминируемых стратегий
равна нулю.
.
Исключение из платежной матрицы
доминируемых стратегий (ими игрокам
пользоваться заведомо невыгодно)
позволяет уменьшить ее размерность, а
это упрощает решение игры. Вероятность
применения доминируемых стратегий
равна нулю.
Оптимальные смешанные стратегии
![]() и
и![]() в игре с платежной матрицей
в игре с платежной матрицей![]() и
ценойvостаются оптимальными и для
игры с платежной матрицей
и
ценойvостаются оптимальными и для
игры с платежной матрицей![]() (гдеb> 0) и ценойbv
+ с. На этом основании платежную матрицу
можно всегда преобразовать так, что ее
элементы будут целыми неотрицательными
числами, а это упрощает расчеты.
(гдеb> 0) и ценойbv
+ с. На этом основании платежную матрицу
можно всегда преобразовать так, что ее
элементы будут целыми неотрицательными
числами, а это упрощает расчеты.
Пример
Упростить следующую платежную матрицу.
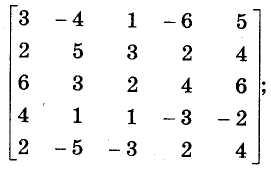
Методы решения матричных игр. Решение матричной игры сведением к задаче линейного программирования
Пусть игра задана платежной матрицей.
|
|
|
|
… |
|
|
|
|
|
… |
|
|
|
|
|
… |
|
|
|
… |
… |
… |
… |
|
|
|
|
… |
|
Оптимальные смешанные стратегии
![]() и
и![]() игроков А и В могут быть найдены в
результате решения пары двойственных
задач линейного программрования.
игроков А и В могут быть найдены в
результате решения пары двойственных
задач линейного программрования.
Для игрока А:

В результате решения задачи находятся
оптимальный вектор
![]() и
и![]() ,
а затем
,
а затем![]() .
.
Для игрока В:

Решая задачу , находят оптимальный
вектор
![]() и
и![]() ,
а затем
,
а затем![]() .
.
Пример
|
1 |
3 |
5 |
7 |
1 |
|
7 |
4 |
3 |
1 |
1 |
|
4 |
4 |
4 |
3 |
3 |
|
7 |
4 |
5 |
7 |
|
Проверим наличие седловой точки.
Для игрока А: Max(1, 1, 3) = 3
Для игрока В: min(7, 4, 5, 7) = 4
Так как значения не совпадаю, Седловой точки нет, а цена игры Vнаходится в промежутке [3; 4].
Решим задачу в смешанных стратегиях. Для этого составим пару двойственных задач.

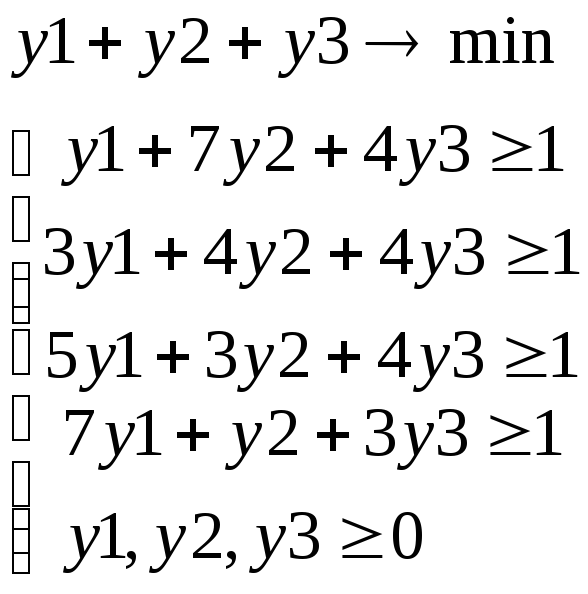
Решая задачи, находим, что
X={0.05, 0.15, 0, 0.07}
Y={0.07, 0.05, 0.15}
F=0.27
Отсюда находим цену игры и вероятности применения стратегий
V=1/0.27=3.7
P={0.19, 0.56, 0.26}
Q={0.26, 0.19, 0.56}
