
- •7.Метод Гаусса
- •5. Решение систем линейных уравнений по формулам Крамера.
- •6.Обратная матрица. Решение систем линейных уравнений матричным способом.
- •8. Арифметические векторы. Линейные операции над векторами.
- •9. Линейная зависимость векторов.
- •11.Скалярное произведение векторов
- •12.Геометрическая интерпретация векторов .
- •13.Линия на плоскости.
- •15. Уравнение прямой проходящей через точку параллельно вектору. Уравнения прямой проходящей через 2 точки.
- •17. Уравнение прямой, проходящей через точку в заданном направлении.
- •16. Уравнение прямой с угловым коэффициентом.
- •18.Угол между двумя прямыми. Условия параллельности и перпендикулярности двух прямых.
- •19. Линии 2-го порядка.
- •21.Угол между 2 прямыми. Условия параллельности и перпендикулярности двух прямых.
- •22.Прямая в пространстве. Угол между 2 прямыми в пространстве. Условия параллельности и перпендикулярности 2 прямых.
- •25. Свойства пределов и правила вычисления приделов. Функция f(X) в точке х0 может иметь только один предел.
- •27.Правила вычисления производных:
- •28. Асимнтоты.
- •29. Возрастание, убывание и экстремумы функций
- •3. Определители 2-ого и 3-его порядка.
9. Линейная зависимость векторов.
Пусть
дана система из mn
– мерных векторов ( ).
Векторы системы * наз. линейно-зависимыми,
если сущ. числа (
).
Векторы системы * наз. линейно-зависимыми,
если сущ. числа ( )
из которых хотя бы одно отлично от нуля
и такие что
)
из которых хотя бы одно отлично от нуля
и такие что
α1 +
α2
+
α2 +
… + αm
+
… + αm =
=
 .
Система векторов наз. линейно-независимой,
если сущ. числа α1=α2=
… = αm=0,
такие что α1
.
Система векторов наз. линейно-независимой,
если сущ. числа α1=α2=
… = αm=0,
такие что α1 +
α2
+
α2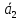 +
… + αm
+
… + αm =
=
 .
.
Св-ва
систем: 1) Если в системе векторов имеется
 ,
то система линейно-зависима; 2) Если к
системе линейно-зависимых векторов
добавить произвольный
,
то система линейно-зависима; 2) Если к
системе линейно-зависимых векторов
добавить произвольный ,
то новая расширенная система будет
также линейно-зависима; 3) Если из
линейно-зависимой системы векторов
удалить любой вектор, то получ. новая
расширенная система будет также
линейно-независимой; 4) Система векторов
состоящая из 2-х и более векторов явл.
линейно-зависимой, тогда и только тогда,
когда хотя бы 1 из векторов системы явл.
линейной комбинацией остальных – это
св-во явл. критерием линейной зависимости
векторов. Два не нулевых вектора
,
то новая расширенная система будет
также линейно-зависима; 3) Если из
линейно-зависимой системы векторов
удалить любой вектор, то получ. новая
расширенная система будет также
линейно-независимой; 4) Система векторов
состоящая из 2-х и более векторов явл.
линейно-зависимой, тогда и только тогда,
когда хотя бы 1 из векторов системы явл.
линейной комбинацией остальных – это
св-во явл. критерием линейной зависимости
векторов. Два не нулевых вектора и
и наз. калинеарными, если они линейно-зависимы
наз. калинеарными, если они линейно-зависимы – условие калинеарности в векторной
форме.
– условие калинеарности в векторной
форме. – условие калинеарности в координатной
форме (если векторы калинеарны, то их
координаты пропорциональны, верна и
обратная). Три не нулевых вектора а, в и
с наз. комплонарными, если они
линейно-зависимы.
– условие калинеарности в координатной
форме (если векторы калинеарны, то их
координаты пропорциональны, верна и
обратная). Три не нулевых вектора а, в и
с наз. комплонарными, если они
линейно-зависимы.
10.Базис и ранг системы векторов.Разложение вектора по заданному базису. Базисам данной системы вектора наз. максимальная подсистема векторы которой линейно-независимы. Теорема: Любой вектор системы может быть разложен по базису единственном образом. Коэффициенты разложения вектора по базису наз.координатами вектора в данном базисе. Один и тот же вектор в разных базисах имеет разные координаты. Рас.nn-мерных векторов след.вида:
 1=(1,0,0,0…..,0)
1=(1,0,0,0…..,0)
 2=(0,1,0,….,0)
2=(0,1,0,….,0)
 3=(0,0,1….0)
3=(0,0,1….0)
 n=(0,0,0,….1)
n=(0,0,0,….1)
Эти
вектора линейно-независимы т.к.равенство
α1 1+
1+ 2
2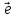 2+α3
2+α3 3+……..αn
3+……..αn n=
n= при условии что α1=α2=α3=…….αn
и все они нули.Такая система векторов
наз.стандартном базисом пространства
Rn.
при условии что α1=α2=α3=…….αn
и все они нули.Такая система векторов
наз.стандартном базисом пространства
Rn.
Ранг
системы-это количество векторов в базисе
этой системы.Для нахождения ранга
системы векторов удобно пользоваться
методом Гаусса при этом условия
α1 1+α2
1+α2 2+……+αn
2+……+αn n=
n= записываем в виде системы линейных
уравнений относительно неизвестных
α1,α2,…..,αn
и решаем эту систему. Число базисных
переменных полученных после прямого
хода равно рангу системы.
записываем в виде системы линейных
уравнений относительно неизвестных
α1,α2,…..,αn
и решаем эту систему. Число базисных
переменных полученных после прямого
хода равно рангу системы.
Имеется
система векторов
 1,
1, 2,…,
2,…, nєRn
которая является линейно-независимой,
нужно вектор в є Rn
разложить по данному базису, т.е.представить
вектор в след. виде α1
nєRn
которая является линейно-независимой,
нужно вектор в є Rn
разложить по данному базису, т.е.представить
вектор в след. виде α1 1+α2
1+α2 2+……+αm
2+……+αm mт.е.нужно
найти координаты
mт.е.нужно
найти координаты
 в данном базисе, а значит найти числа
α1,α2,…..,αm.Для
этого векторного уравнения запишем в
координатной форме (векторы записываем
в виде столбцов) получим систему уравнений
которую решим методом Гаусса.
в данном базисе, а значит найти числа
α1,α2,…..,αm.Для
этого векторного уравнения запишем в
координатной форме (векторы записываем
в виде столбцов) получим систему уравнений
которую решим методом Гаусса.
11.Скалярное произведение векторов
Скалярное
произведение 2-х n-мерных
вектора
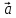 =(
=( ,
, 2….аn)
и
2….аn)
и
 =(
=( 1,
1, 2…
2… n)
наз-ся число равное сумме произведений
соотв-х координат данных векторов
обоз-ся:
n)
наз-ся число равное сумме произведений
соотв-х координат данных векторов
обоз-ся:
 *
* =
= 1
1 1+
1+ 2
2 2+….+
2+….+ n
n n
n
Св-ва скалярного произведения:
1. =
=
2.( +
+ )*
)* =
= +
+
3.α( )=(α
)=(α )
) =
= (α
(α )
)
4.(α +β
+β )
) =α(
=α( )+β(
)+β( )
)
5. *
*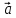 =
= 2≥0
2≥0
Модулем
или длиной вектора
 наз-ся
число: │
наз-ся
число: │ 2│=
2│= 2=
2=
Вектор
 наз-ся единичным,если его длина=1,т.е.
│
наз-ся единичным,если его длина=1,т.е.
│ │=1
│=1
Система
вектора
 1,
1, 2,…
2,… mназ-сянормированой,если
она состоит из единых векторов.Базис
из единых верторовназ-ся нормированным
базисом.
mназ-сянормированой,если
она состоит из единых векторов.Базис
из единых верторовназ-ся нормированным
базисом.
Векторы
 и
и наз-ся
ортогональным(перпендикулярным)если:
наз-ся
ортогональным(перпендикулярным)если: *
* .
.
Векторы стандартного базиса состоят из взаимно ортогональных единых векторов.
Ортогональный базис — базис, составленный из попарно ортогональных векторов.
Любая ортогональная система состоит из не нулевых векторов линейно независима.
