5.1 Нерівність трикутника

Нехай на площина задано трикутник ABC.

Тодісправедливінаступнінерівності. Згеометричнихміркувань дана рівність очевидно правильна.

2. НерівністьКоші

Нехай заданідійсні числа та. Тоді для них справедлива нерівність:

2. НерівністьКоші-Буняковського

Нехай заданідійсні числа та. Тоді для них справедлива нерівність

ДоведенняРозглянемотакінерівності

Додамоліві і правічастинивідповідно, отримаємо:

Перепозначимо:

Отримаємонерівність і розв’яжемоїї:

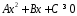
Зостанньоїнерівностімаємо:

Що і потрібнобуло довести.

2. Нерівність Єнсена

Дана нерівність по праву займає фундаментальне місце серед решти нерівностей, оскільки за допомогою неї можна довести значну кількість нерівностей (в тому числі і класичних).

Якщо функція опукла на деякому проміжку, то мають місце нерівності:

• для функції, опуклої вниз:

,

• для функції, опуклої вгору:

,

де - довільні дійсні числа з цього проміжку,. Рівність досягається лише в одному з двох випадків:— лінійна функція або.

Ці формули значно спрощуються, якщо .

• Для функції опуклої вниз

• Для функції опуклої вгору

Найчастіше використовується окремий випадок нерівностей Єнсена при .

• для функції, опуклої вниз:

• для функції, опуклої вгору:

2. Нерівність Гельдера

Нехай задані числа таp,q такі, щоТоді для них справедлива нерівність:

РОЗДІЛ ІІ. МЕТОДИКА ФОРМУВАННЯ ТА РОЗВИТОК ВМІНЬ УЧНІВ ДОВЕДЕННЯ ЧИСЛОВИХ НЕРІВНОСТЕЙ