4.6. Методи диференціального числення.

Застосування методів диференціального числення для доведення не­рівностей базується в основному на таких принципах:

• використання властивостей монотонних функцій;

• використання властивостей опуклих функцій.

Теорема 1. Якщо іна інтервалі, при­чому функціянеперервна на інтервалі, то функція набуває надодатних (від'ємних) значень.

Дійсно, функція зростаюча (спадна) на цьому інтервалі, бо , тому примаємо:.

Приклад 12. Довести нерівність Бернуллі для довільних

а)при;

б) при.

Доведення. Розглянемо функцію , це неперервна і диференційована функція на,.

При або,, тому функціязростає для, отже,, тобто виконується нерівність. При,, тому функціяспадна для, отже,, тобто виконується нерівність.

Методами диференціального числення можна довести класичну не­рівність Коші, найважче при цьому — дібрати відповідну функцію.

Приклад 13. Довести нерівність Коші 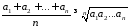, якщоневід’ємні числа.

Доведення. Введемо такі позначення:

.

Розглянемо функцію . Для неї виконуються рівностіта. Нам потрібно довести, що. Знайдемо похідну цієї функції. Очевидно, що. Друга похідна цієї функції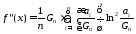додатна, тому функціязростає на, тобто. Оскільки, то функціязростає на. Таким чином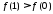. Тобто нерівність Коші виконується.

Теорема 2. Якщо функція визначена і монотонна на відрізку, то найменшого й найбільшого значень функція набуває на кінцях відрізка.

Теорема 3. Якщо неперервна функція на відрізкумає одну точку екстремуму, то у випадку мінімуму найбільшого значення функція набуває на кінцях відрізка (властивість А), а у випадку максимуму най­меншого значення функція набуває на кінцях відрізка (властивість Б).

Приклад 14. Доведіть, що, якщо.

Доведення. Зауважимо відразу, що при маємо рівність для всіх, тому вважатимемо, що. Функціянеперервна і диференційована на, причому. Знайдемо похіднуі легко впевнимося, щопри— це точка мінімуму і. Таким чином,. Отже, для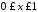маємо нерівність —. У правій частині рівність досягається приі.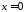

Теорема 4 (Теорема Лагранжа). Якщо функціянеперервна на відрізкудиферен­ційована на інтервалі, то існує принаймні одне число, для якого виконується умова.

Якщо функція зростає на, тоі маємо нерівність.

Приклад 15. Доведіть нерівність , якщо.

Доведення. Функція неперервна й диференційована на будь-якому відрізку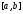, тому для неї виконується теорема Лагранжа, тобто має місце рівність

,

Де. Оскільки функціязростаюча в області визначення, то. Врахувавши останню нерівність, дістанемо нерівність, що й треба було довести.

§5. Класичні нерівності

Класичні нерівності

Класичні нерівності є могутнім джерелом різноманітних нерівностей, з одного боку, а з іншого — вони часто,використовуються для доведення багатьох нерівностей. Деякі з них особливо багаті наслідками. На мою думку, незаслужено мало уваги в математичній літературі, присвяченій нерівностям, звертається на нерівність Чебишова. Використання формул деяких скінченних сум у поєднанні з нерівністю Чебишова дозволяє дістати цілу низку цікавих нерівностей лише показникових і логарифмічних. Ці ідеї можуть бути розвинуті й далі для інших класів функцій, інших скінченних сум тощо.