§3. Місце теми в шкільному курсі математики

У загальноосвітній школі в класах рівня стандарту вивчення теми «Доведення нерівностей» не передбачено. Програма для класів з поглибленим вивченням математики передбачає вивчення теми «Нерівності» у 8 класі. Такий підхід дозволяє під час вивчення тем «Властивості квадратного кореня», «Розв’язування рівнянь з модулем», «Побудова графіків функцій» звернути увагу учнів на необхідність постійно мати на увазі множину допустимих значень виразів, які входять до рівнянь, а також відслідковувати перетворення, які можуть вплинути на множину допустимих значень змінних (розширити чи звузити її) у ході розв’язування рівнянь. Зазначене дозволяє суттєво урізноманітнити зміст завдань. На відміну від загальноосвітніх класів, вивчення теми «Нерівності» багато в чому спирається на апарат теорії множин, вивчений у відповідній темі, зокрема, запис розв’язків має виконуватися з використанням символіки теорії множин. Програма для класів з поглибленим вивченням математики передбачає вивчення теми «Доведення нерівностей» у 9 класі.

§4. Основні методи доведення нерівностей

Розглянуті методи доведення нерівностей, зазвичай, не використовуються самостійно, а використовуються одночасно для доведення однієї нерівності.

1. Аналітичний метод

За означенням вважається, що , якщо різниця- невід’ємне число. Тому для доведення нерівності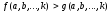на заданій множині значеньнеобхідно скласти різницюі впевнитися в тому, що вона невід’ємна при заданих значеннях(аналогічно застосовують цей спосіб для доведення нерівностей виду).

Приклад 1. Доведемо, що якщо , то

(нерівність Коші) (1)

Доведення. Складемо різницю . Зрозуміло, що виразневід’ємне при будь-яких додатних значенняхa i b. Значить, і різниця невід’ємна, а це означає, що. Відмітимо, що знак рівності має місце тільки при.

Приклад 2. Доведемо, що якщо ,

то . (2)

Доведення. Маємо: 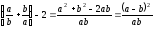. Так як, то, причому знак рівності має місце тільки при. Отже, різницяневід’ємна, тобто нерівність (2) доведена.

Приклад 3. Доведемо, що якщо , то

(3)

Доведення. Розглянемо різницю , в якій сумудоповнимо до куба суми. Отримаємо :

Розклавши суми кубів на множники, отримаємо:

Так як за умовою , то отриманий вираз невід’ємний. Звідси випливає істинність нерівності (3). Причому знак рівності в нерівності (3) має місце при, а також коли.

2. Синтетичний метод

Суть цього методу заключається в тому, що за допомогою ряду перетворень нерівність, яку потрібно довести виводять з деяких відомих (опорних) нерівностей. В якості опорних можуть використовуватися, наприклад, такі нерівності:

А) ;

Б) ;

В), де;

Г), деі.

Приклад 4. Доведемо, що якщо то

(4)

Доведення. Візьмемо у якості опорної нерівність Коші:

.

Так як, і, то. Звідси, але, таким чином.

Проаналізувавши доведення, приходимо до висновку, що знак рівності в нерівності (4) має місце тоді і тільки тоді, коли і, тобто коли.

Приклад 5. Доведемо, що якщо , то(5).

Доведення. 1-ий спосіб. Візьмемо в якості опорних наступні нерівності:

(ці нерівності перетворюються у рівність, коли відповідно . Додавши їх, отримаємо, або. Виконавши ряд нескладних перетворень

Винесемо () за дужки, отримаємо:. Знак рівності має місце у випадку, колиa=b=c.

2- й спосіб. Нерівність (5) можна довести за означенням. Маємо

Отже, нерівність (5) справедлива.

Приклад 6. Доведемо, що якщо , то

(6)

Доведення. Маємо:

Додамо ці рівності, їх (n-1) штук, отримаємо:

Отже .