Показатели вариаций.
Для измерения вариации признака в
математической статистике используется:
вариационный размах (
); среднее квадратичное отклонение (
);
дисперсия признака (
),
коэффициент вариации (
).
Для грубого оценивания рассеяния вариант
признака относительно
применяют вариационный размах, который
равен
.
Для характеристики меры вариации вокруг средней арифметической применяются следующие числовые характеристики: среднее линейное отклонение, дисперсия, среднее квадратическое отклонение, коэффициент вариации по среднему квадратическому отклонению.
Определение. Средним линейным отклонением вариационного ряда называется средняя арифметическая абсолютных величин отклонений вариантов от их средней арифметической
.
Определение. Дисперсией
вариационного ряда называется средняя
арифметическая квадратов отклонений
вариант признака от их средней
арифметической взвешенной
или
Можно доказать, что
Из определения дисперсии следует, что ее размерность равна квадрату размерности признака, что составляет некоторое неудобство в применении.
Определение. Средним квадратическим отклонением называется корень квадратный из дисперсии
,
Т.к. среднее квадратическое отклонение имеет размерность, равную размерности признака, то оно является более удобной, а поэтому и чаще применяемой на практике характеристикой рассеяния признака.
Определение. Коэффициентом вариации по среднему квадратическому отклонениюназывается величина, которая вычисляется по формуле
Коэффициент вариации по среднему квадратическому отклонению служит для сравнения оценок вариаций статистических рядов.
Можно показать, что для арифметической средней и дисперсии признака имеет место упрощенный способ их расчета, аналогичный методу моментов, доказанному в теории вероятностей.
Теорема
,
,
где 
Пример.По заданному дискретному вариационному ряду:
-
2,5
4,5
6,5
8,5
10,5
10
20
30
30
10
вычислить:
а) 
;
б)
;
в) 
.
Если признак задан интервальным
вариационным рядом, то формуле деления
отрезка пополам находим
-
середины интервалов, т.е.
.
Следует отметить, что эти характеристики в математической статистике называются статистическими и их определения, а также свойства аналогичны используемым в теории вероятностей при одном только условии, что в определениях слово «вероятность» заменяется словом «частость».
Пример.По заданному интервальному вариационному ряду
-
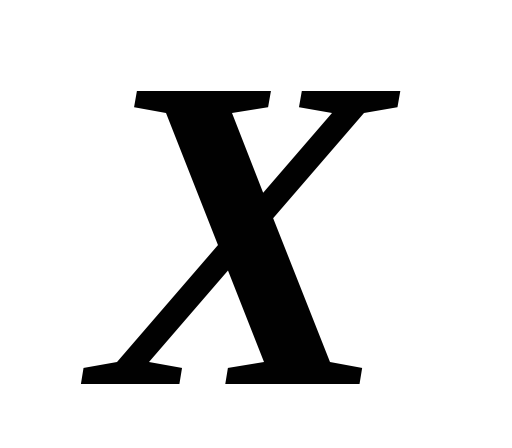
0-4
4-5
8-12
12-16
16-20
20-24
6
14
20
25
30
5
Вычислить:
1.
;
2.
.