
Тема 13. Кратні інтеграли
|
ІЗ – 13.1 |
|
1 |
Змінити порядок інтегрування |
1.1. ![]()
1.2. ![]()
1.3. ![]()
1.4. ![]()
1.5.![]()
1.6.![]()
1.7.![]()
1.8.![]()
1.9.![]()
1.10. ![]()
1.11. ![]()
1.12. ![]()
1.13. ![]()
1.14. ![]()
1.15. ![]()
1.16. ![]()
1.17. ![]()
1.18. ![]()
1.19. ![]()
1.20. ![]()
1.21. ![]()
1.22. ![]()
1.23. 
1.24. ![]()
1.25. ![]()
1.26. ![]()
1.27. ![]()
1.28. ![]()
1.29. ![]()
1.30. ![]()
|
2 |
Розставити границі інтегрування двома способами, якщо область |
|
|
D подана зазначеними лініями |
2.1. ![]()
![]() ;
;![]() ;
;![]()
2.2. ![]()
![]() ;
;![]()
![]()
2.3. ![]()
![]() ;
;![]() ;
;![]()
2.4. ![]()
![]() ;
;![]() ;
;![]() ;
;![]()
2.5. ![]()
![]() ;
;![]()
2.6. ![]()
![]() ;
;![]()
2.7. ![]()
![]() ;
;![]() ;
;![]() ;
;![]()
2.8. ![]()
![]() -2;
-2;![]()
2.9. ![]()
![]() ;
;![]() ;
;![]() ;
;![]()
2.10. ![]()
![]() ;
;![]() ;
;![]()
2.11. ![]()
![]() ;
;![]() ;
;![]()
2.12. ![]()
![]() ;
;![]()
2.13. ![]()
![]() ;
;![]() ;
;![]()
2.14. ![]()
![]() ;
;![]() ;
;![]()
2.15. ![]()
![]() ;
;![]() ;
;![]() ;
;![]()
2.16. ![]()
![]() ;
;![]() ;
;![]()
2.17. ![]()
![]() ;
;![]() ;
;![]()
2.18. ![]()
![]() ;
;![]()
2.19. ![]()
![]() ;
;![]() ;
;![]() ;
;![]()
2.20. ![]()
![]() ;
;![]() ;
;![]() ;
;![]()
2.21. ![]()
![]() ;
;![]() ;
;![]()
2.22. ![]()
![]() ;
;![]() ;
;![]() ;
;![]()
2.23. ![]()
![]() ;
;![]()
2.24. ![]()
![]() ;
;![]() ;
;![]() ;
;![]()
2.25. ![]()
![]() ;
;![]() ;
;![]() ;
;![]()
2.26. ![]()
![]() ;
;![]() ;
;![]()
2.27. ![]()
![]() ;
;![]() ;
;![]() ;
;![]()
2.28. ![]()
![]() ;
;![]() ;
;![]()
2.29. ![]()
![]() ;
;![]() ;
;![]()
2.30. ![]()
![]() ;
;![]() ;
;![]() ;
;![]()
|
3 |
Обчислити подвійний інтеграл по області D, обмеженої вказаними |
|
|
лініями |
|
3.1. |
|
|
|
3.2. |
|
|
|
3.3. |
|
|
|
3.4. |
|
|
|
3.5. |
|
|
|
3.6. |
|
|
|
3.7. |
|
|
|
3.8. |
|
|
|
3.9. |
|
|
|
3.10. |
|
|
|
3.11. |
|
|
|
3.12. |
|
|
|
3.13. |
|
|
|
3.14. |
|
|
|
3.15. |
|
|
|
3.16. |
|
|
|
3.17. |
|
|
|
3.18. |
|
|
|
3.19. |
|
|
|
3.20. |
|
|
|
3.21. |
|
|
|
3.22. |
|
|
|
3.23. |
|
|
|
3.24. |
|
|
|
3.25. |
|
|
|
3.26. |
|
|
|
3.27. |
|
|
|
3.28. |
|
|
|
3.29. |
|
|
|
3.30. |
|
|
|
4 |
Обчислити подвійний інтеграл у полярних координатах |
|
|
|
4.1.
![]() 4.2.
4.2.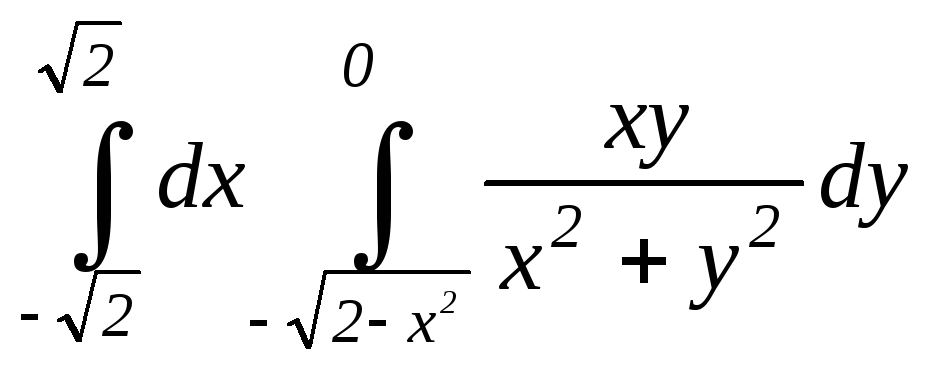
4.3.
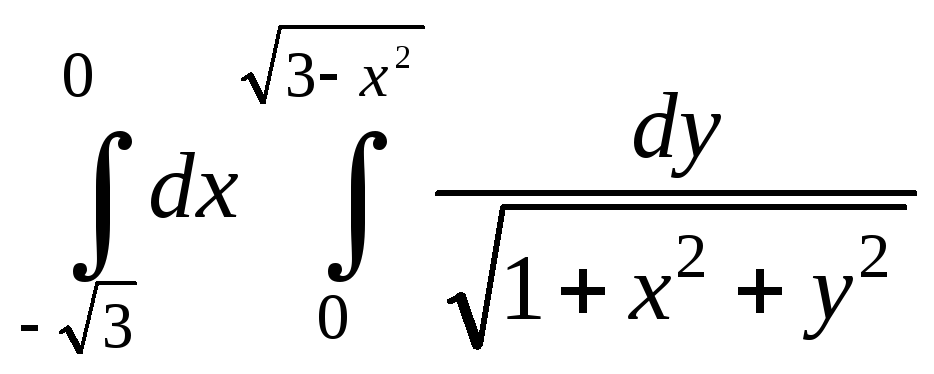 4.4.
4.4.![]()
4.5.
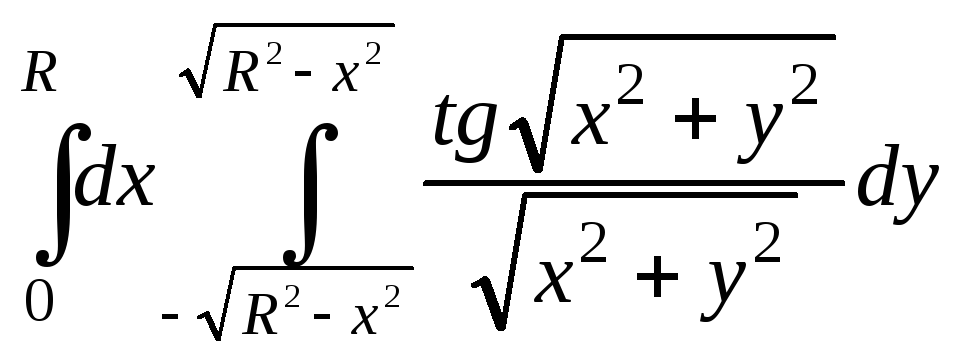 4.6.
4.6.![]()
4.7.
![]() 4.8.
4.8.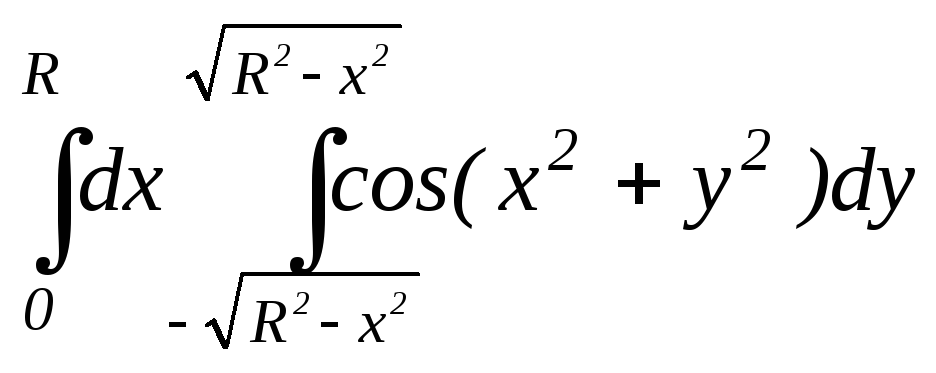
4.9.
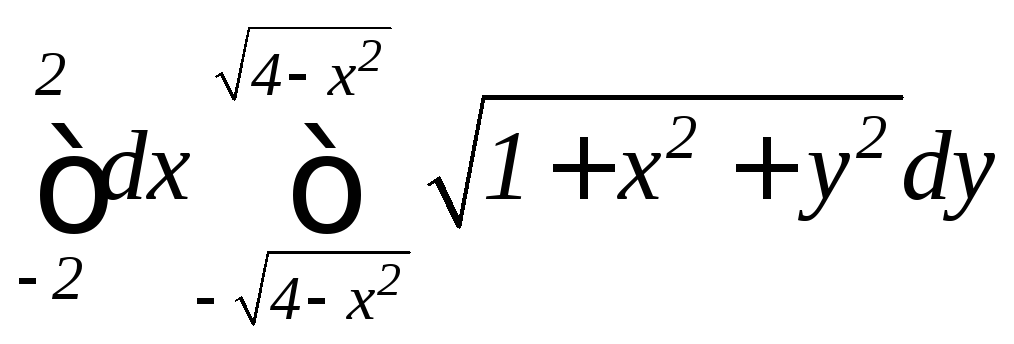 4.10.
4.10.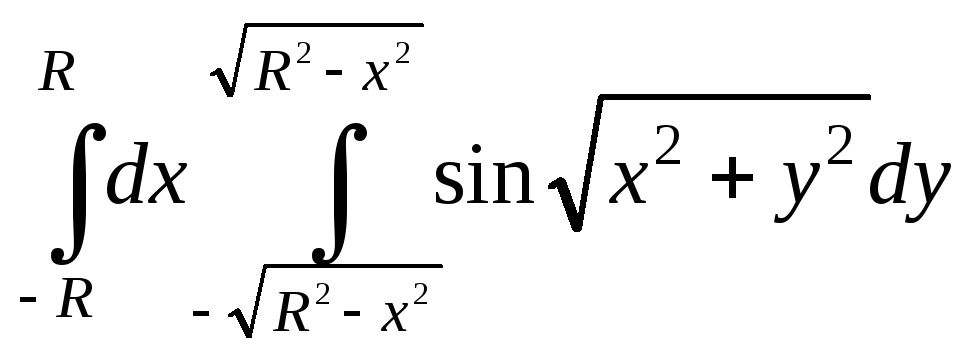
4.11.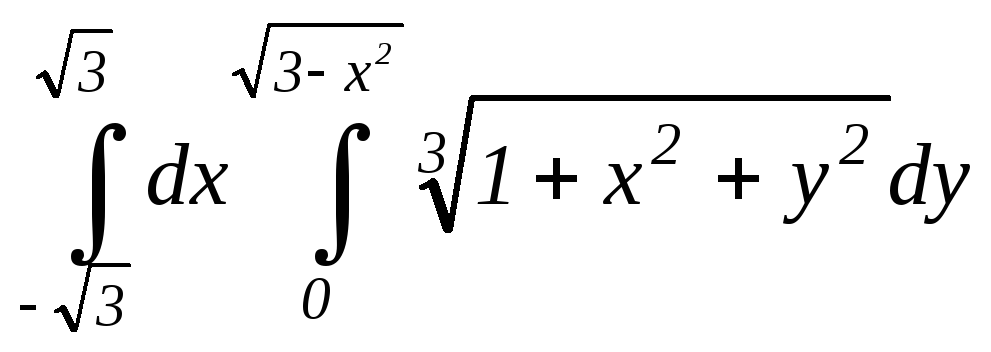 4.12.
4.12.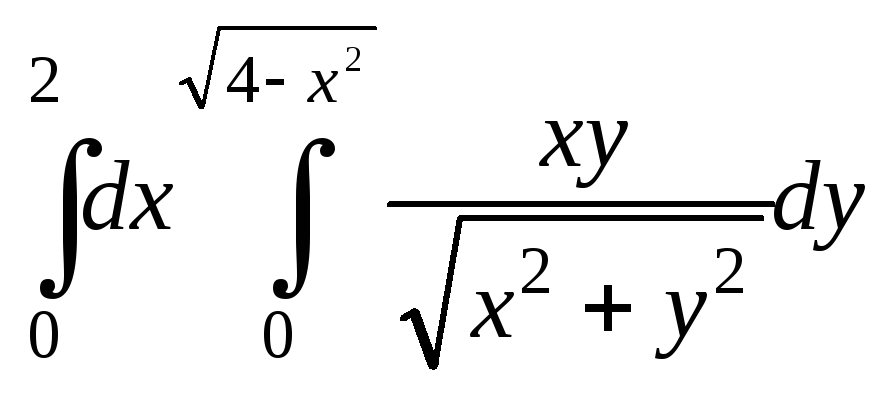
4.13.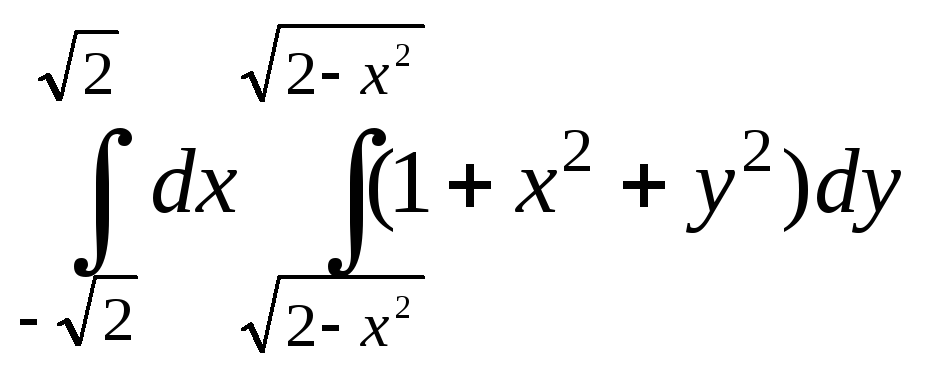 4.14.
4.14.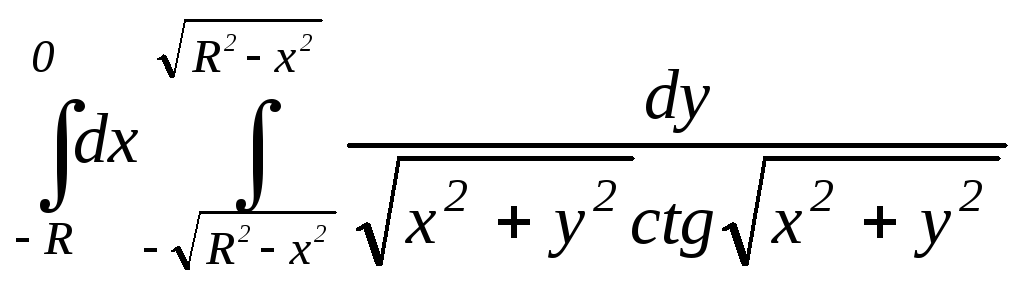
4.15.
![]() 4.16.
4.16.![]()
4.17.
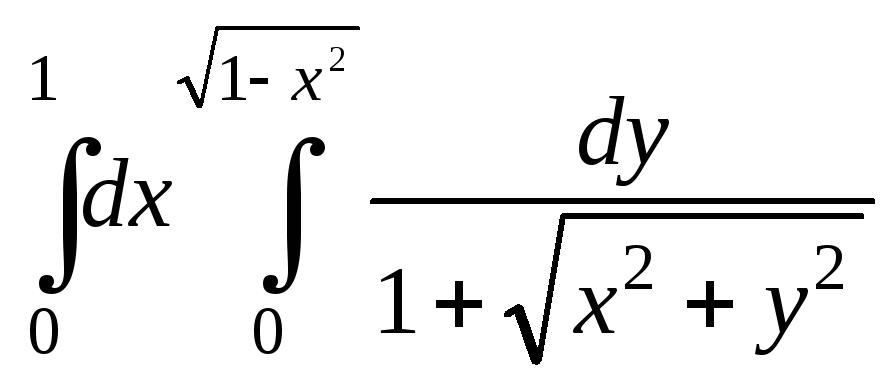 4.18.
4.18.![]()
4.19.
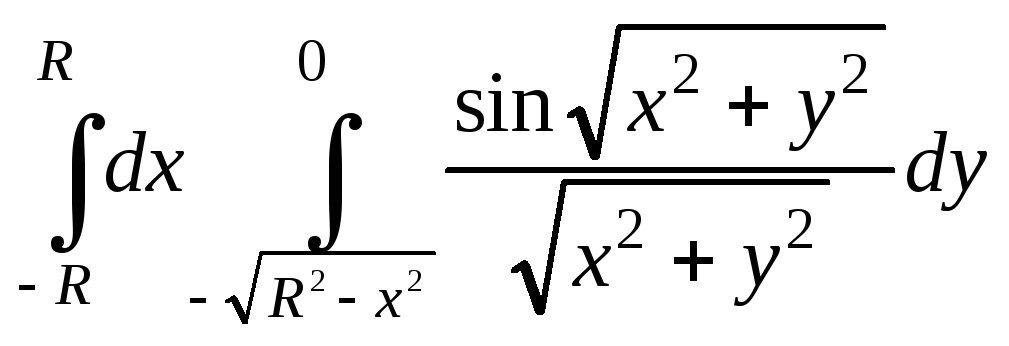 4.20.
4.20.![]()
4.21.
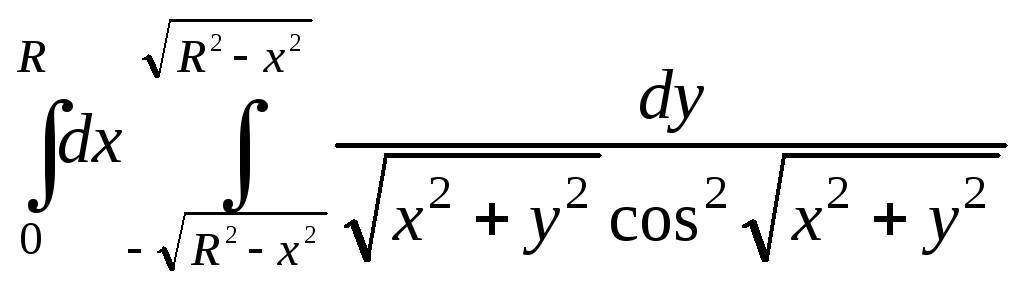 4.22.
4.22.
![]()
4.23.
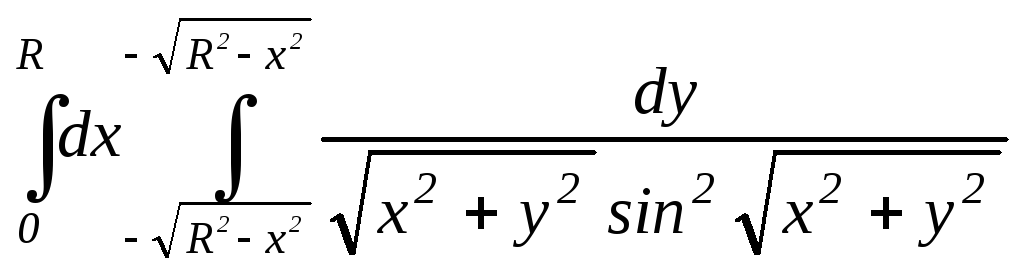 4.24.
4.24.
![]()
4.25.
![]() 4.26.
4.26.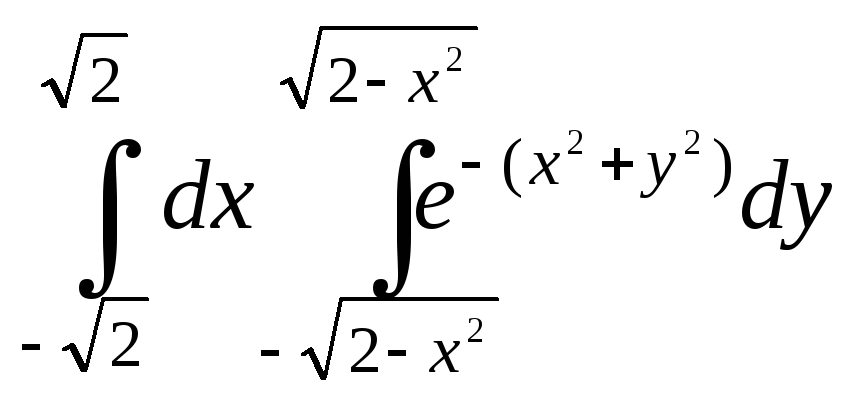
4.27.
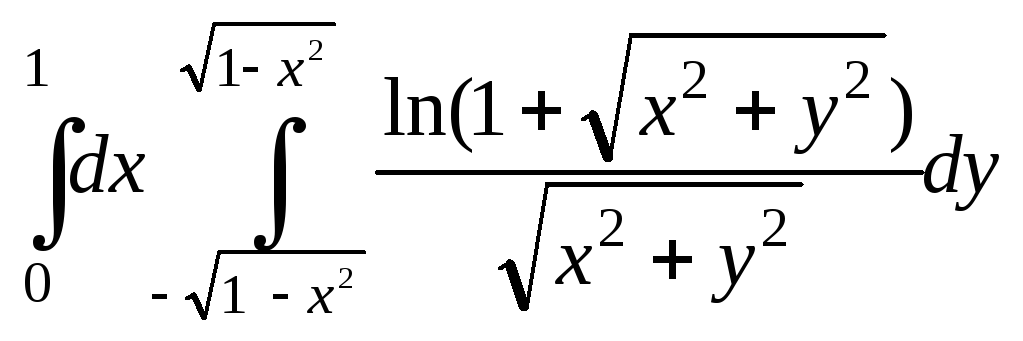 4.28.
4.28.![]()
4.29.
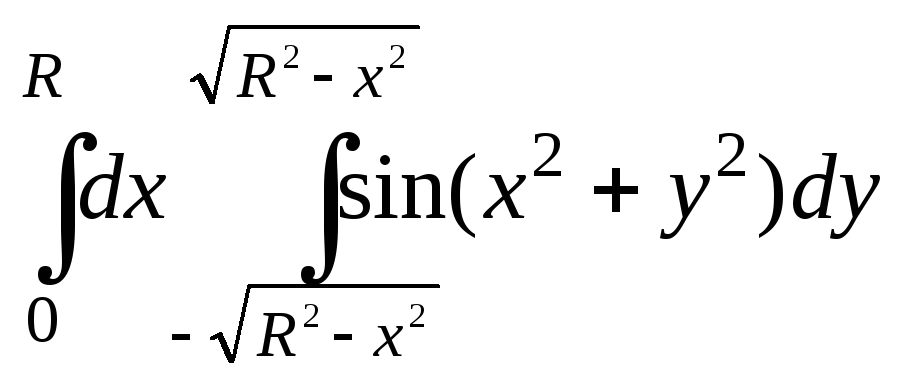 4.30.
4.30.![]()
|
5 |
Обчислити площу плоскої фігури D, обмеженої зазначеними |
|
|
лініями |
5.1.
![]() 5.2.
5.2.![]()
5.3.
![]() 5.4.
5.4.![]()
5.5.
![]() 5.6.
5.6.![]()
5.7.
![]() 5.8.
5.8.![]()
5.9.
![]() 5.10.
5.10.
![]()
5.11 ![]() 5.12
5.12
![]()
5.13 ![]() 5.14
5.14
![]()
5.15 ![]() 5.16
5.16
![]()
5.17 ![]() 5.18
5.18
![]()
5.19 ![]() 5.20
5.20
![]()
5.21 ![]() 5.22
5.22
![]()
5.23
![]() 5.24
5.24![]()
5.25
![]() 5.26
5.26![]()
5.27
![]() 5.28
5.28![]()
5.29
![]() 5.30
5.30![]()
|
6 |
За допомогою подвійних інтегралів обчислити у полярних |
|
|
координатах площу плоскої фігури, обмеженої зазначеними |
|
|
лініями (а > 0) |
6.1.
![]() 6.16.
6.16.![]()
6.2.
![]() 6.17.
6.17.![]()
6.3.
![]() 6.18.
6.18.![]()
6.4
![]() 6.19.
6.19.![]()
6.5.
![]() 6.20.
6.20.![]()
6.6.
![]() 6.21.
6.21.![]()
6.7.
![]() 6.22.
6.22.![]()
6.8.
![]() 6.23.
6.23.![]()
6.9.
![]() 6.24.
6.24.![]()
6.10.
![]() 6.25.
6.25.![]()
6.11.
![]() 6.26.
6.26.![]()
6.12.
![]() 6.27.
6.27.
![]()
6.13.
![]() 6.28.
6.28.![]()
6.14.
![]() 6.29.
6.29.![]()
6.15.
![]() 6.30.
6.30.![]()
|
7 |
Обчислити об’єм тіла, обмеженого зазначеними поверхнями |
|
|
|
7.1. ![]()
7.2. ![]()
7.3. ![]()
7.4. ![]()
7.5. ![]()
7.6. ![]()
7.7. ![]()
7.9. ![]()
7.10. ![]()
7.11. ![]()
7.12. ![]()
7.13. ![]()
7.14. ![]()
7.15. ![]()
7.16. ![]()
7.17. ![]()
7.18. ![]()
7.19. ![]()
7.20. ![]()
7.21. ![]()
7.23. ![]()
7.24. ![]()
7.25. ![]()
7.26. ![]()
7.27. ![]()
7.28. ![]()
7.29. ![]()
7.30. ![]()
|
ІЗ – 13.2 |
|
1 |
Розставити границі інтегрування в потрійному інтегралі |
|
|
|
|
|
поверхнями. Побудувати область інтегрування |
1.1. ![]()
1.2. ![]()
1.3. ![]()
1.4. ![]()
1.5. ![]()
1.6. ![]()
1.7. ![]()
1.8. ![]()
1.9. ![]()
1.10. ![]()
1.11. ![]()
1.12. ![]()
1.13. ![]()
1.14. ![]()
1.15. ![]()
1.16. ![]()
1.17. ![]()
1.18. ![]()
1.19. ![]()
1.20. ![]()
1.21. ![]()
1.22. ![]()
1.23. ![]()
1.24. ![]()
1.25. ![]()
1.26. ![]()
1.27. ![]()
1.28. ![]()
1.29. ![]()
1.30. ![]()
|
2 |
Обчислити потрійний інтеграл
від функції
|
|
|
|
| ||
|
2.1. |
|
|
|
|
|
2.2. |
|
|
|
|
|
2.3. |
|
|
|
|
|
2.4. |
|
|
|
|
|
2.5. |
|
|
|
|
|
2.6. |
|
|
|
|
|
2.7. |
|
|
|
|
|
2.8. |
|
|
|
|
|
2.9. |
|
|
|
|
|
2.10. |
|
|
|
|
|
2.11. |
|
|
|
|
|
2.12. |
|
|
|
|
|
2.13. |
|
|
|
|
|
2.14. |
|
|
|
|
|
2.15. |
|
|
|
|
|
2.16. |
|
|
|
|
|
2.17. |
|
|
|
|
|
2.18. |
|
|
|
|
|
2.19. |
|
|
|
|
|
2.20. |
|
|
|
|
|
2.21. |
|
|
|
|
|
2.22. |
|
|
|
|
|
2.23. |
|
|
|
|
|
2.24. |
|
|
|
|
|
2.25. |
|
|
|
|
|
2.26. |
|
|
|
|
|
2.27. |
|
|
|
|
|
2.28. |
|
|
|
|
|
2.29. |
|
|
|
|
|
2.30. |
|
|
|
|
|
3 |
Обчислити потрійний інтеграл
від функції
|
|
|
|
|
|
|
|
|
3.1. |
|
|
|
3.2. |
|
|
|
3.3. |
|
|
|
3.4. |
|
|
|
3.5. |
|
|
|
3.6. |
|
|
|
3.7. |
|
|
|
3.8. |
|
|
|
3.9. |
|
|
|
3.10. |
|
|
|
3.11. |
|
|
|
3.12. |
|
|
|
3.13. |
|
|
|
3.14. |
|
|
|
3.15. |
|
|
|
3.16. |
|
|
|
3.17. |
|
|
|
3.18. |
|
|
|
3.19. |
|
|
|
3.20. |
|
|
|
3.21. |
|
|
|
3.22. |
|
|
|
3.23. |
|
|
|
3.24. |
|
|
|
3.25. |
|
|
|
3.26. |
|
|
|
3.27. |
|
|
|
3.28. |
|
|
|
3.29. |
|
|
|
3.30. |
|
|
|
4 |
За допомогою потрійного інтеграла обчислити об’єм тіла, |
|
|
обмеженого зазначеними поверхнями. Побудувати тіло |
4.1. ![]() ,
,![]()
4.2. ![]() ,
,![]() ,
,![]() ,
,![]()
4.3. ![]() ,
,![]() ,
,![]()
4.4. ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
4.5. ![]() ,
,![]() ,
,![]()
4.6. ![]() ,
,![]() ,
,![]() ,
,![]()
4.7. ![]() ,
,![]() ,
,![]() ,
,![]()
4.8. ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
4.9. ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
4.10. ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
4.11. ![]() ,
,![]() ,
,![]()
4.12. ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
4.13
. ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
4.14. ![]() ,
,![]() ,
,![]() ,
,![]()
4.15. ![]() ,
,![]() ,
,![]()
4.16
. ![]() ,
,![]() ,
,![]()
4.17
. ![]() ,
,![]() ,
,![]()
4.18
. ![]() ,
,![]() ,
,![]() ,
,![]()
4.19. ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
4.20. ![]() ,
,![]() ,
,![]()
4.21. ![]() ,
,![]() ,
,![]()
4.22. ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
4.23. ![]() ,
,![]() ,
,![]()
4.24. ![]() ,
,![]() ,
,![]() ,
,![]()
4.25. ![]() ,
,![]() ,
,![]() ,
,![]()
4.26. ![]() ,
,![]() ,
,![]() ,
,![]()
4.27. ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
4.28. ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
4.29. ![]() ,
,![]() ,
,![]()
4.30. ![]() ,
,![]() ,
,![]() ,
,![]()
|
ІЗ – 13.3 |
|
1 |
Обчислити масу неоднорідної матеріальної пластини D, |
|
|
обмеженої зазначеними лініями, якщо поверхнева щільність в |
|
|
кожній її точці
|
|
|
|
|
|
1.1. |
|
|
|
1.2. |
|
|
|
1.3. |
|
|
|
1.4. |
|
|
|
|
|
|
|
1.5. |
|
|
|
1.6. |
|
|
|
1.7. |
|
|
|
1.8. |
|
|
|
1.9. |
|
|
|
1.10. |
|
|
|
1.11. |
|
|
|
1.12. |
|
|
|
1.13. |
|
|
|
1.14. |
|
|
|
1.15. |
|
|
|
1.16. |
|
|
|
1.17. |
|
|
|
1.18. |
|
|
|
1.19. |
|
|
|
1.20. |
|
|
|
1.21. |
|
|
|
1.22. |
|
|
|
1.23. |
|
|
|
1.24. |
|
|
|
1.25. |
|
|
|
1.26. |
|
|
|
1.27. |
|
|
|
1.28. |
|
|
|
1.29. |
|
|
|
1.30. |
|
|
|
2 |
Обчислити статичний момент однорідної матеріальної пластини |
|
|
D, обмеженої зазначеними лініями відносно поданої вісі |
|
|
координат, використовуючи полярні координати |
|
|
|
Вісь |
|
2.1. |
|
|
|
2.2. |
|
|
|
2.3. |
|
|
|
2.4. |
|
|
|
2.5. |
|
|
|
2.6. |
|
|
|
2.7. |
|
|
|
2.8. |
|
|
|
2.9. |
|
|
|
2.10. |
|
|
|
2.11. |
|
|
|
2.12. |
|
|
|
2.13. |
|
|
|
2.14. |
|
|
|
2.15. |
|
|
|
2.16. |
|
|
|
2.17. |
|
|
|
2.18. |
|
|
|
2.19. |
|
|
|
2.20. |
|
|
|
2.21. |
|
|
|
2.22. |
|
|
|
2.23. |
|
|
|
2.24. |
|
|
|
2.25. |
|
|
|
2.26. |
|
|
|
2.27. |
|
|
|
2.28. |
|
|
|
2.29 |
|
|
|
2.30. |
|
|
|
3 |
Обчислити
координати центра мас однорідного
тіла
|
|
|
зазначеними поверхнями |
|
3 |
Обчислити момент інерції однорідного тіла V відносно зазначеної |
|
|
вісі координат, обмеженого поданими поверхнями. Щільність |
|
|
тіла
|
|
|
|
Вісь |
|
|
|
Вісь |
|
4.1. |
|
|
|
4.2. |
|
|
|
4.3. |
|
|
|
4.4. |
|
|
|
4.5. |
|
|
|
4.6. |
|
|
|
4.7. |
|
|
|
4.8. |
|
|
|
4.9. |
|
|
|
4.10. |
|
|
|
4.11. |
|
|
|
4.12. |
|
|
|
4.13. |
|
|
|
4.14. |
|
|
|
4.15. |
|
|
|
4.16. |
|
|
|
4.17. |
|
|
|
4.18. |
|
|
|
4.19. |
|
|
|
4.20. |
|
|
|
4.21. |
|
|
|
4.22. |
|
|
|
4.23. |
|
|
|
4.24. |
|
|
|
4.25. |
|
|
|
4.26. |
|
|
|
4.27. |
|
|
|
4.28. |
|
|
|
4.29. |
|
|
|
4.30. |
|
|
ЗМІСТ
|
ВСТУП . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
3 | |
|
|
|
|
|
ТЕМА 10. |
ДИФЕРЕНЦІАЛЬНЕ ЧИСЛЕННЯ ФУНКЦІЙ БАГАТЬОХ ЗМІННИХ. . . . . . . . . . . . . . . . . . . . . . |
4 |
|
|
|
|
|
ТЕМА 11. |
ЗВИЧАЙНІ ДИФЕРЕНЦІАЛЬНІ РІВНЯННЯ . . . |
15 |
|
|
|
|
|
ТЕМА 12. |
ЕЛЕМЕНТИ ОПЕРАЦІЙНОГО ЧИСЛЕННЯ . . . |
32 |
|
|
|
|
|
ТЕМА 13. |
КРАТНІ ІНТЕГРАЛИ . . . . . . . . . . . . . . . . . . . . . . . |
42 |
Навчальне видання
ІНДИВІДУАЛЬНІ ЗАВДАННЯ З ВИЩОЇ МАТЕМАТИКИ
Частина 3
Укладачі: Печеніжський Юрій Євгенович
Станішевський Степан Олександрович
Данилевський Микола Прокопович
Кадець Михайло Йосипович
Відповідальний за випуск А.І. Колосов
Редактор М.З. Аляб’єв
План 2007, поз. 30 М
_____________________________________________________________
Підписано до друку 25.09. 2007 р. Формат 60х84 1/16 Папір офісний
Друк на ризографі Умов. друк. арк. 3,7 Обл.-вид. арк. 4,0
Тираж 300 прим. Зам. №
_____________________________________________________________
