
Тема 11. Звичайні диференціальні рівняння
|
ІЗ – 11.1 |
|
1 |
Знайти загальний розв’язок (загальний інтеграл) |
|
|
диференціального рівняння |
1.1.
![]() 1.2.
1.2.![]()
1.3.
![]() 1.4.
1.4.![]()
1.5.![]() 1.6.
1.6.![]()
1.7.
![]() 1.8.
1.8.![]()
1.9.
![]() 1.10.
1.10.![]()
1.11.![]() 1.12.
1.12.![]()
1.13.![]() 1.14.
1.14.![]()
1.15.![]() 1.16.
1.16.![]()
1.17.![]() 1.18.
1.18.![]()
1.19.
![]() 1.20.
1.20.![]()
1.21.![]() 1.22.
1.22.![]()
1.23.![]() 1.24.
1.24.![]()
1.25.
![]() 1.26.
1.26.![]()
1.27.![]() 1.28.
1.28.![]()
1.29.![]() 1.30.
1.30.![]()
|
2 |
Знайти загальний розв’язок |
 2.2.
2.2.
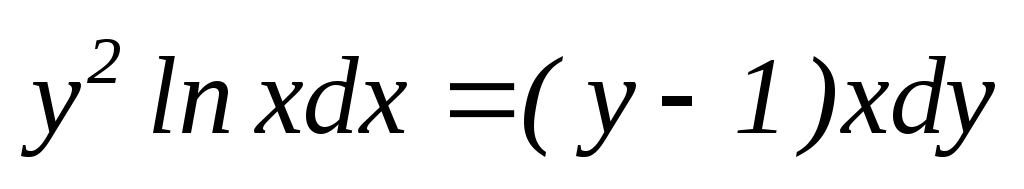
2.3.
![]() 2.4.
2.4.![]()
2.5.
![]() 2.6.
2.6.![]()
2.7.
![]() 2.8.
2.8.![]()
2.9.
![]() 2.10.
2.10.![]()
2.11.
![]() 2.12.
2.12.![]()
2.13.
![]() 2.14.
2.14.![]()
2.15.
![]() 2.16.
2.16.![]()
2.17.
![]() 2.18.
2.18.![]()
2.19.
![]() 2.20.
2.20.![]()
2.21.
![]() 2.22.
2.22.![]()
2.23.
![]() 2.24.
2.24.![]()
2.25.
![]() 2.26.
2.26.![]()
2.27.
![]() 2.28.
2.28.![]()
2.29.
![]() 2.30.
2.30.![]()
|
3 |
Знайти загальний розв’язок |
3.1.
![]() 3.2.
3.2.![]()
3.3.
![]() 3.4.
3.4.![]()
3.5.
![]() 3.6.
3.6.![]()
3.7.
![]() 3.8.
3.8.![]()
3.9.
![]() 3.10.
3.10.![]()
3.11.
![]() 3.12.
3.12.![]()
3.13.![]() 3.14.
3.14.
![]()
3.15.
![]() 3.16.
3.16.![]()
3.17.
![]() 3.18.
3.18.![]()
3.19.
![]() 3.20.
3.20.![]()
3.21.
![]() 3.22.
3.22.![]()
3.23.
![]() 3.24.
3.24.![]()
3.25.
![]() 3.26.
3.26.![]()
3.27.![]() 3.28.
3.28.![]()
3.29.
![]() 3.30.
3.30.![]()
![]()
|
4 |
Знайти частинний розв’язок (частинний інтеграл) |
|
|
диференціального рівняння, задовольняючий початковій умові |
4.1.
![]()
![]()
4.2.
![]()
![]()
4.3.
![]()
![]()
4.4.
![]()
![]()
4.5.
![]()
![]()
4.6.
![]()
![]()
4.7.
![]()
![]()
4.8.
![]()
![]()
4.9.
![]()
![]()
4.10.
![]()
![]()
4.11.
![]()
![]()
4.12.
![]()
![]()
4.13.
![]()
![]()
4.14.
![]()
![]()
4.15.
![]()
![]()
4.16.
![]()
![]()
4.17.
![]()
![]()
4.18.
![]()
![]()
4.19.
![]()
![]()
4.20.
![]()
![]()
4.21.
![]()
![]()
4.22.
![]()
![]()
4.23.
![]()
![]()
4.24.
![]()
![]()
4.25.
![]()
![]()
4.26.
![]()
![]()
4.27.
![]()
![]()
4.28.
![]()
![]()
4.29.
![]()
![]()
4.30.
![]()
![]()
|
5 |
Знайти загальний розв’язок диференціального рівняння |
5.1.
![]() 5.2.
5.2.![]()
5.3.
![]() 5.4.
5.4.![]()
5.5.
![]() 5.6.
5.6.![]()
5.7.
![]() 5.8.
5.8.![]()
5.9.
![]() 5.10.
5.10.![]()
5.11.
![]() 5.12.
5.12.![]()
5.13.
![]() 5.14.
5.14.![]()
5.15.
![]() 5.16.
5.16.![]()
5.17.
![]() 5.18.
5.18.![]()
5.19.
![]() 5.20.
5.20.![]()
5.21.
![]() 5.22.
5.22.![]()
5.23.
![]() 5.24.
5.24.![]()
5.25.
![]() 5.26.
5.26.![]()
5.27.
![]() 5.28.
5.28.![]()
5.29.
![]() 5.30.
5.30.![]()
|
ІЗ – 11.2 |
|
1 |
Знайти частинний розв’язок диференціального рівняння, який |
|
|
задовольняє початковим умовам і обчислити значення одержаної |
|
|
функції
|
1.1.
![]()
![]()
1.2.
![]()
![]()
1.3.
![]()
![]()
1.4.
![]()
![]()
1.5.
![]()
![]()
1.6.
![]()
![]()
1.7.
![]()
![]()
1.8.
![]()
![]()
1.9.
![]()
![]()
1.10.
![]()
![]()
1.11.
![]()
![]()
1.12.
![]()
![]()
1.13.
![]()
![]()
1.14.
![]()
![]()
1.15.
![]()
![]()
1.16.
![]()
![]()
1.17.
![]()
![]()
1.18.
![]()
![]()
1.19.
![]()
![]()
1.20.
![]()
![]()
1.21.
![]()
![]()
1.22.
![]()
![]()
1.23.
![]()
![]()
1.24.
![]()
![]()
1.25.
![]()
![]()
1.26.![]()
![]()
1.27.
![]()
![]()
1.28.
![]()
![]()
1.29.
![]()
![]()
1.30.
![]()
![]()
|
2 |
Знайти загальний розв’язок диференціального рівняння, яке |
|
|
дозволяє зниження порядку |
|
2.1.
2.2.
2.3.
2.4.
2.5.
2.6.
2.7.
2.8.
2.9.
2.10.
2.11.
2.12.
2.13.
2.14.
2.15.
|
2.16.
2.17.
2.18.
2.19.
2.20.
2.21.
2.22.
2.23.
2.24.
2.25.
2.26.
2.27.
2.28.
2.29.
2.30.
|
|
3 |
Розв’язати задачу Коші для диференціального рівняння, яке |
|
|
дозволяє зниження порядку |
3.1.
![]()
![]()
3.2.
![]()
![]()
3.3.
![]()
![]()
3.4.
![]()
![]()
3.5.
![]()
![]()
3.6.
![]()
![]()
3.7.
![]()
![]()
3.8.
![]()
![]()
3.9.
![]()
![]()
3.10.
![]()
![]()
3.11.
![]()
![]()
3.12.
![]()
![]()
3.13.
![]()
![]()
3.14.
![]()
![]()
3.15.
![]()
![]()
3.16.
![]()
![]()
3.17.
![]()
![]()
3.18.
![]()
![]()
3.19.
![]()
![]()
3.20.
![]()
![]()
3.21.
![]()
![]()
3.22.
![]()
![]()
3.23.
![]()
![]()
3.24.
![]()
![]()
3.25.
![]()
![]()
3.26.
![]()
![]()
3.27.
![]()
![]()
3.28.
![]()
![]()
3.29.
![]()
![]()
3.30.
![]()
![]()
|
4 |
Знайти загальний розв’язок диференціального рівняння |
|
|
|
4.1.
![]()
4.2.
![]()
4.3.
![]()
4.4.
![]()
4.5.
![]()
4.6.
![]()
4.7.
![]()
4.8.
![]()
4.9.
![]()
4.10.
![]()
4.11.
![]()
4.12.
![]()
4.13.
![]()
4.14.
![]()
4.15.
![]()
4.16.
![]()
4.17.
![]()
4.18.
![]()
4.19.
![]()
4.20.
![]()
4.21.
![]()
4.22.
![]()
4.23.
![]()
4.24.
![]()
4.25.
![]()
4.26.
![]()
4.27.
![]()
4.28.
![]()
4.29.
![]()
4.30.
![]()
|
ІЗ – 11.3 |
|
1 |
Знайти загальний розв’язок диференціального рівняння |
|
|
|
1.1. а)
![]() б)
б)![]() в)
в)![]()
1.2. а)
![]() б)
б)
![]() в)
в)![]()
1.3. а)
![]() б)
б)![]() в)
в)![]()
1.4. а)
![]() б)
б)![]() в)
в)![]()
1.5. а)
![]() б)
б)![]() в)
в)![]()
1.6. а)
![]() б)
б)![]() в)
в)![]()
1.7. а)
![]() б)
б)![]() в)
в)![]()
1.8. а)
![]() б)
б)![]() в)
в)![]()
1.9. а)
![]() б)
б)![]() в)
в)![]()
1.10. а)
![]() б)
б)![]() в)
в)![]()
1.11. а)
![]() б)
б)![]() в)
в)![]()
1.12. а)
![]() б)
б)![]() в)
в)![]()
1.13. а)
![]() б)
б)![]() в)
в)![]()
1.14. а)
![]() б)
б)![]() в)
в)![]()
1.15. а)
![]() б)
б)![]() в)
в)![]()
1.16. а)
![]() б)
б)![]() в)
в)![]()
1.17. а)
![]() б)
б)![]() в)
в)![]()
1.18. а)
![]() б)
б)![]() в)
в)![]()
1.19. а)
![]() б)
б)![]() в)
в)![]()
1.20. а)
![]() б)
б)![]() в)
в)![]()
1.21. а)
![]() б)
б)![]() в)
в)![]()
1.22. а)
![]() б)
б)![]() в)
в)![]()
1.23. а)
![]() б)
б)![]() в)
в)![]()
1.24. а)
![]() б)
б)![]() в)
в)![]()
1.25. а)
![]() б)
б)![]() в)
в)![]()
1.26. а)
![]() б)
б)![]() в)
в)![]()
1.27. а)
![]() б)
б)![]() в)
в)![]()
1.28. а)
![]() б)
б)![]() в)
в)![]()
1.29. а)
![]() б)
б)![]() в)
в)![]()
1.30. а)
![]() б)
б)![]() в)
в)![]()
|
2 |
Знайти загальний розв’язок диференціального рівняння |
|
2.1.
|
2.2.
|
|
2.3.
|
2.4.
|
|
2.5.
|
2.6.
|
|
2.7.
|
2.8.
|
|
2.9.
|
2.10.
|
|
2.11.
|
2.12.
|
|
2.13.
|
2.14.
|
|
2.15.
|
2.16.
|
|
2.17.
|
2.18.
|
|
2.19.
|
2.20.
|
|
2.21.
|
2.22.
|
|
2.23.
|
2.24.
|
|
2.25.
|
2.26.
|
|
2.27.
|
2.28.
|
|
2.29.
|
2.30.
|
|
3 |
|
|
3.1.
|
3.2.
|
|
3.3.
|
3.4.
|
|
3.5.
|
3.6.
|
|
3.7.
|
3.8.
|
|
3.9.
|
3.10.
|
|
3.11.
|
3.12.
|
|
3.13.
|
3.14.
|
|
3.15.
|
3.16.
|
|
3.17.
|
3.18.
|
|
3.19.
|
3.20.
|
|
3.21.
|
3.22.
|
|
3.23.
|
3.24.
|
|
3.25.
|
3.26.
|
|
3.27.
|
3.28.
|
|
3.29.
|
3.30.
|
|
4 |
Знайти частинний розв’язок диференційного рівняння, який |
|
|
задовольняє початковим умовам |
4.1.
![]()
![]()
4.2.
![]()
![]()
4.3.
![]()
![]()
4.4.
![]()
![]()
4.5.
![]()
![]()
4.6.
![]()
![]()
4.7.
![]()
![]()
4.8.
![]()
![]()
4.9.
![]()
![]()
4.10.
![]()
![]()
4.11.
![]()
![]()
4.12.
![]()
![]()
4.13.
![]()
![]()
4.14.
![]()
![]()
4.15.
![]()
![]()
4.16.
![]()
![]()
4.17.
![]()
![]()
4.18.
![]()
![]()
4.19.
![]()
![]()
4.20.
![]()
![]()
4.21.
![]()
![]()
4.22.
![]()
![]()
4.23.
![]()
![]()
4.24.
![]()
![]()
4.25.
![]()
![]()
4.26.
![]()
![]()
4.27.
![]()
![]()
4.28.
![]()
![]()
4.29.
![]()
![]()
4.30.
![]()
![]()
|
5 |
Визначити і записати структуру частинного розв’язку |
|
|
лінійного неоднорідного диференціального рівняння другого |
|
|
порядку зі сталими коефіцієнтами для двох варіантів функції, яка |
|
|
стоїть праворуч |
|
|
|
| |
|
|
|
а) |
б) |
|
5.1. |
|
|
|
|
5.2. |
|
|
|
|
5.3. |
|
|
|
|
5.4. |
|
|
|
|
5.5. |
|
|
|
|
5.6. |
|
|
|
|
5.7. |
|
|
|
|
5.8. |
|
|
|
|
5.9. |
|
|
|
|
5.10. |
|
|
|
|
5.11. |
|
|
|
|
5.12. |
|
|
|
|
5.13. |
|
|
|
|
5.14. |
|
|
|
|
5.15. |
|
|
|
|
5.16. |
|
|
|
|
5.17. |
|
|
|
|
5.18. |
|
|
|
|
5.19. |
|
|
|
|
5.20. |
|
|
|
|
5.21. |
|
|
|
|
5.22. |
|
|
|
|
5.23. |
|
|
|
|
5.24. |
|
|
|
|
5.25. |
|
|
|
|
5.26. |
|
|
|
|
5.27. |
|
|
|
|
5.28. |
|
|
|
|
5.29. |
|
|
|
|
5.30. |
|
|
|
|
6 |
Розв’язати систему диференціальних рівнянь методом |
|
|
зведення її до диференціального рівняння вищого порядку |
6.1.
![]() 6.2.
6.2.![]()
6.3.
![]() 6.4.
6.4.![]()
6.5.
![]() 6.6.
6.6.![]()
6.7.
![]() 6.8.
6.8.![]()
6.9.
![]() 6.10.
6.10.![]()
6.11.
![]() 6.12.
6.12.![]()
6.13.
![]() 6.14.
6.14.![]()
6.15.
![]() 6.16.
6.16.![]()
6.17.
![]() 6.18.
6.18.![]()
6.19.
![]() 6.20.
6.20.![]()
6.21.
![]() 6.22.
6.22.![]()
6.23.
![]() 6.24.
6.24.![]()
6.25.
![]() 6.26.
6.26.![]()
6.27.
![]() 6.28.
6.28.![]()
6.29.
![]() 6.30.
6.30.![]()
|
7 |
Розв’язати неоднорідне диференціальне рівняння другого порядку |
|
|
методом варіації довільних сталих |
7.1.
![]() 7.2.
7.2.![]()
7.3.
![]() 7.4.
7.4.![]()
7.5.
![]() 7.6.
7.6.![]()
7.7.
![]() 7.8.
7.8.![]()
7.9.
![]() 7.10.
7.10.![]()
7.11.
![]() 7.12.
7.12.![]()
7.13.
![]() 7.14.
7.14.![]()
7.15.
![]() 7.16.
7.16.![]()
7.17.
![]() 7.18.
7.18.![]()
7.19.
![]() 7.20.
7.20.![]()
7.21.
![]() 7.22.
7.22.![]()
7.23.
![]() 7.24.
7.24.![]()
7.25.
![]() 7.26.
7.26.![]()
7.27.
![]() 7.28.
7.28.![]()
7.29.
![]() 7.30.
7.30.![]()
