1.9. Скалярний та векторний добуток векторів

Скалярний та векторний добуток векторів дуже важливі у фізиці. Багато фізичних величин є скалярними чи векторними добутками від інших величин. Якщо два вектора перемножимо скалярно, то отримаємо число (скалярну величину), а якщо перемножимо векторно – вектор.

1.9.1. Скалярний добуток векторів

Нехай є два вектори і:

,

.

Скалярний добуток цих векторів позначається абоі дорівнює сумі добутків відповідних компонент двох векторів:

.

Скалярний добуток векторів ідорівнює добутку модулів двох векторівr і  на косінус кута між векторами :

.

Властивості скалярного добутку:

1) множники можна переставляти місцями ;

2) можна розкривати дужки ;

3) якщо вектори ненульової довжини (0 та R0) та їхній скалярний добуток , то ці вектори взаємно перпендикулярні.

1.9.2. Векторний добуток векторів

Розглянемо знову введені раніше вектори і. Векторним добутком цих векторів є такий вектор (див. рис. 1.11), який задовольняє таким умовам:

1) модуль вектора дорівнює добутку модулів векторів іна синус кута між ними;

2) і, тобто вектор перпендикулярний до площини, в якій лежать вектори і;

3) трійка векторів , і– права у правій системі координат.

Трійкою векторів будемо називати задані у певній послідовності три некомпланарні (які не лежать в одній площині) вектори.

Трійка векторів , іназивається правою, якщо дивимося із кінця вектора і бачимо найкорочше обертання від до, що відбувається проти годинникової стрілки. Декартова система координат називається правою, якщо складена з ортів системи координат трійка векторів є правою.

Векторний добуток позначається квадратними дужками або знаком “”:

.

Властивості векторного добутку:

1) важливим є порядок множників (тобто вектори, що визначаються векторними добуткамиімають протилежний напрямок);

2) модуль векторного добутку векторів ічисельно рівний площі паралелограма, утвореного цими векторами (див. рис. 1.11):

;

Рис. 1.11

3) векторний добуток двох ненульових векторів дорівнює нулю , якщо вектори паралельні. Символпозачає нульовий вектор (усі три проекції вектора на координатні осі дорівнюють нулю).

Інколи векторний добуток двох векторів іпредставляють у вигляді визначника, верхній рядок якого складається з ортів координатних осей ; другий і третій рядки – з проекцій на координатні осі векторів і:

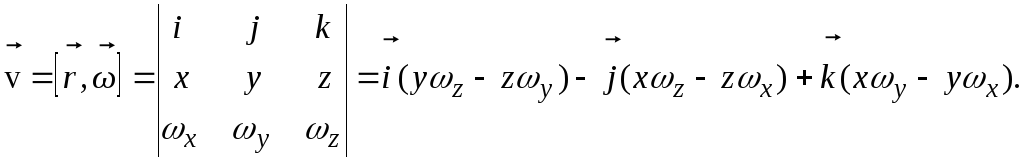
1.10. Зв’язок лінійних кінематичних величин із кутовими

Розглянемо точку А, яка належить тілу, що обертається (див. рис. 1.12). Лінійна швидкість точки є векторним добутком векторів кутової швидкості і радіус-вектораточкиА:

.

Якщо провести перпендикулярний до осі обертання вектор в дану точку тіла, то, оскільки вектор швидкості перпендикулярний до площини, в якій лежать вектори і, можна записати

.

Модуль лінійної швидкості дорівнює

v =  R.

Тангенціальне й нормальне прискорення виражаються через кутові величини таким чином:

,

.

Рис.1.12