Сопромат. 1-10

			1
			2

Решение: При косом изгибе нормальное напряжение в точке поперечного сечения с координатами x, y определяется по формуле  В сечении, в котором расположены точки В и С, значения изгибающих моментов, соответственно, равны    Осевые моменты инерции сечения относительно главных центральных осей 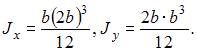 В точке В с координатами  нормальное напряжение 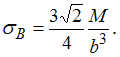 В точке С с координатами  нормальное напряжение  Следовательно, отношение 

  ЗАДАНИЕ N 18 сообщить об ошибке Тема: Изгиб с кручением Стержень квадратного сечения со стороной b нагружен моментами. Значение эквивалентного напряжения в опасных точках, по теории наибольших касательных напряжений, равно _________. При решении принять 

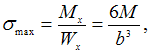
Решение: Стержень работает на чистый изгиб и кручение. В любом поперечном сечении стержня действуют изгибающий  и крутящий  моменты. В точках В и С возникают максимальные, по абсолютной величине, нормальные напряжения   Касательные напряжения в точках В и С также равны и определяются по формуле Эквивалентное напряжение в опасных точках В и С, по теории наибольших касательных напряжений, определим по формуле После подстановки  и  найдем

  ЗАДАНИЕ N 19 сообщить об ошибке Тема: Виды нагружения стержня Схема нагружения рамы круглого поперечного сечения показана на рисунке. Участок рамы I испытывает …

			чистый изгиб и растяжение
			поперечный изгиб и растяжение
			поперечный изгиб и кручение
			кручение и растяжение

Решение: Произвольным поперечным сечением на первом участке делим раму на две части. Отбросим левую часть. Рассмотрим равновесие правой оставшейся части. Из уравнений статики следует, что в поперечном сечении возникают: продольная сила N, изгибающие моменты  и  Для круглого сечения  и поэтому косой изгиб можно свести к плоскому с моментом  Следовательно, первый участок испытывает чистый изгиб и растяжение.

  ЗАДАНИЕ N 20 сообщить об ошибке Тема: Изгиб с растяжением?сжатием Стержень квадратного сечения со стороной b нагружен двумя силами F. Если изменить направление одной из сил на противоположное, то значение максимального нормального напряжения …

			увеличивается в 3 раза
			станет равным нулю
			увеличивается в 2 раза
			уменьшается в 2 раза

Решение: В первом варианте нагружения стержень работает на растяжение и максимальное нормальное напряжение  При смене направления одной из сил на противоположное стержень работает на чистый изгиб. Максимальное нормальное напряжение определяется по формуле Следовательно, максимальное нормальное напряжение в стержне увеличивается в три раза.

  ЗАДАНИЕ N 1 сообщить об ошибке Тема: Изгиб с кручением Схема нагружения круглого стержня диаметром , длиной  показана на рисунке. Значение допускаемого нормального напряжения для материала, одинаково работающего на растяжение и сжатие, . Максимальное значение силы F, которую можно приложить к стержню, из расчета по напряжениям равно ___ Н. При решении задачи использовать теорию наибольших касательных напряжений (III теорию прочности).

			245
			490
			350
			195

Решение: Опасное сечение стержня расположено вблизи заделки, где возникает изгибающий момент   и крутящий момент  Значение эквивалентного напряжения в опасной точке стержня, по теории наибольших касательных напряжений, определяется по формуле   где  Учитывая, что  найдем  Из условия прочности по напряжениям  найдем  После вычислений получим 

  ЗАДАНИЕ N 2 сообщить об ошибке Тема: Пространственный и косой изгиб Стержень квадратного сечения нагружен внешними силами F и  Линейные размеры l и b заданы. Нормальное напряжение в точке В равно нулю, когда сила  равна …

			F
			2F
			– F

Решение: При косом изгибе нормальное напряжение в произвольной точке поперечного сечения определяется по формуле где x, y – координаты точки в системе главных центральных осей по абсолютной величине. В поперечном сечении, где расположена точка В, имеем   Учитывая знаки нормальных напряжений в точке В 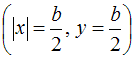, запишем Следовательно, нормальное напряжение в точке В равно нулю при значении 

  ЗАДАНИЕ N 3 сообщить об ошибке Тема: Виды нагружения стержня Схема нагружения рамы показана на рисунке. Первый участок испытывает ____________, второй ____________.

			I – поперечный изгиб, II –кручение
			I – чистый изгиб, II –кручение
			I – поперечный изгиб, II – чистый изгиб
			I – поперечный изгиб, II – поперечный изгиб

Решение: Из анализа внутренних силовых факторов, возникающем на каждом участке, следует: первый участок испытывает плоский поперечный изгиб, второй – кручение.

  ЗАДАНИЕ N 4 сообщить об ошибке Тема: Изгиб с растяжением?сжатием Сила приложена в центре тяжести поперечного сечения по направлению оси стержня. При перемещении силы от центра тяжести, параллельно начальному положению, нормальное напряжение в центре тяжести поперечного сечения …

			остается неизменным
			увеличивается пропорционально расстоянию, на которое переносится сила
			уменьшается пропорционально расстоянию, на которое переносится сила
			увеличивается, когда сила выйдет за границу ядра сечения

Решение: При перемещении силы от центра тяжести сечения стержень испытывает внецентренное растяжение (сжатие). Нормальное напряжение в произвольной точке поперечного сечения определяется по формуле  где x, y – координаты точки в системе главных центральных осей, взятые по абсолютной величине. В центре тяжести поперечного сечения   Следовательно, нормальное напряжение в центре тяжести сечения, при перемещении силы от центра тяжести сечения остаются неизменными.

  ЗАДАНИЕ N 5 сообщить об ошибке Тема: Модели прочностной надежности 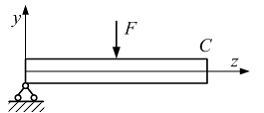Правый конец балки (см. рисунок) необходимо закрепить так, чтобы сечение С не перемещалось вдоль координатных осей z и y, но могло бы поворачиваться в плоскости zy. Опора, отвечающая таким требованиям, называется …

			шарнирно неподвижной
			шарнирно подвижной
			жестким защемлением
			скользящим защемлением

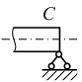
Решение: Опора, отвечающая требованиям задания, называется шарнирно неподвижной. Условное обозначение такой опоры показано на рисунке.

  ЗАДАНИЕ N 6 сообщить об ошибке Тема: Перемещение и деформация В процессе нагружения рамы силой F точка К перемещается вдоль оси x на 3 мм, а вдоль оси y на 2 мм (см. рисунок). Полное перемещение точки Кравно _____ мм.

			3,6
			5
			2,24
			1

Решение: Полное перемещение точки К равно длине отрезка  (см. рисунок). 

  ЗАДАНИЕ N 7 сообщить об ошибке Тема: Внутренние силы и напряжения Числовой мерой распределения внутренних сил по сечению является …

			напряжение
			продольная сила
			потенциальная энергия
			изгибающий момент

Решение: Числовой мерой распределения внутренних сил по сечению является напряжение. Размерность напряжения  В системе СИ напряжение измеряется в Па, кПа, МПа.

  ЗАДАНИЕ N 8 сообщить об ошибке Тема: Основные понятия, определения, допущения и принципы На рисунках показана одна и та же балка, нагруженная силами  и  (рис. 1), силой  (рис. 2), силой  (рис. 3).  – прогибы концевых сечений. Исходя из принципа независимости действия сил можно записать …

Решение: Согласно принципу независимости действия сил результатов действия системы сил равен сумме результатов действий каждой силы в отдельности. Поэтому можно записать 

  ЗАДАНИЕ N 9 сообщить об ошибке Тема: Расчет балок на прочность При плоском изгибе максимальные нормальные напряжения действуют в точках поперечного сечения, …

			наиболее удаленных от нейтральной линии
			лежащих на нейтральной линии
			расположенных в плоскости действия момента
			лежащих в плоскости перпендикулярной действию момента

Решение: Распределение нормальных напряжений по высоте поперечного сечения балки определяется уравнением где  – изгибающий момент в поперечном сечении, в котором определяются нормальные напряжения;  – осевой момент инерции сечения относительно главной центральной оси, перпендикулярной плоскости действия изгибающего момента; y – расстояние от главной центральной оси до точки, в которой определяется нормальное напряжение. Геометрическое место точек в поперечном сечении, где нормальные напряжения равны нулю, называется нейтральной линией. Нейтральная линия совпадает с главной центральной осью сечения x. В конкретном поперечном сечении величины  и  заданы. Переменной является параметр y. При увеличении расстояния y значение  увеличивается. Следовательно, максимальные нормальные напряжения действуют в точках наиболее удаленных от нейтральной линии.

  ЗАДАНИЕ N 10 сообщить об ошибке Тема: Поперечная сила, изгибающий момент и их эпюры Консольная балка длиной  нагружена силами  и  Сечение I–I расположено бесконечно близко в заделке. Изгибающий момент в сечении I–I равен нулю, если значение силы  равно …

Решение: Рассекаем балку в сечении I–I на две части. Отбросим левую часть. Действие отброшенной левой части на оставшуюся заменяем поперечной силой Q и изгибающим моментом М. Составим уравнение равновесия для определения изгибающего момента в сечении I–I Из условия, что в данном сечении , найдем