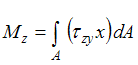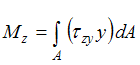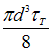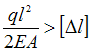Сопромат. 1-10

 ЗАДАНИЕ N 1 сообщить об ошибке Тема: Внутренние силы и напряжения Интегральная связь между крутящим моментом  () и касательными напряжениями имеет вид …

  ЗАДАНИЕ N 2 сообщить об ошибке Тема: Перемещение и деформация Размерность линейной деформации – …

Решение: L – первоначальная длина стержня  – длина стержня после приложения к нему растягивающих сил.  – абсолютное изменение первоначальной длины.  – линейная деформация (величина относительная и безразмерная).

  ЗАДАНИЕ N 3 сообщить об ошибке Тема: Основные понятия, определения, допущения и принципы Материал, у которого при переходе от одной точки к другой свойства, в зависимости от направления, изменяются по одному и тому же закону, является …

			анизотропным, однородным
			изотропным, однородным
			анизотропным, неоднородным
			изотропным, неоднородным

Решение: Материал, у которого свойства зависят от направления, проходящего через точку, называется анизотропным. Материал, у которого закон изменения свойств, при переходе от одной точки к другой, остается постоянным, называется однородным. Следовательно, правильный ответ «данный материал является анизотропным и однородным».

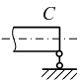
  ЗАДАНИЕ N 4 сообщить об ошибке Тема: Модели прочностной надежности Правый конец балки (см. рисунок) должен быть закреплен таким образом, чтобы сечение С не перемещалось вдоль оси y, но могло бы перемещается вдоль оси z и поворачиваться в плоскости zy. Опора, отвечающая таким требованиям, называется …

			шарнирно подвижной
			скользящим защемлением
			жестким защемлением
			шарнирно неподвижной

Решение: Опора, отвечающая требованиям задания, называется шарнирно подвижной. Условное обозначение такой опоры показано на рисунке.

  ЗАДАНИЕ N 5 сообщить об ошибке Тема: Крутящий момент. Деформации и напряжения 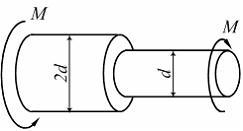В самых напряженных точках поперечного сечения вала касательные напряжения достигнут предела текучести тогда, когда значение момента М равно …

Решение: Максимальные касательные напряжения возникают на правом участке. Значение М, при котором эти напряжения станут равными пределу текучести, определим из условия 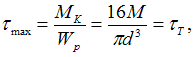 откуда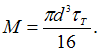 

  ЗАДАНИЕ N 6 сообщить об ошибке Тема: Расчет на жесткость при кручении Максимальный относительный угол закручивания для стержня, показанного на рисунке, равен … Известны величины: М, d, G – модуль сдвига материала стержня.

Решение: Стержень имеет три участка (левый, средний и правый). Относительный угол закручивания определим по формуле  где  и  – крутящий момент и полярный момент инерции поперечного сечения на соответствующем участке. После вычислений получаем:    таким образом 

  ЗАДАНИЕ N 7 сообщить об ошибке Тема: Расчет на прочность при кручении На рисунке показана труба, работающая на кручение. Заданы величины:  предел текучести при чистом сдвиге  Фактический коэффициент запаса из расчета по текучести в самых напряженным точках равен …

			2,1
			1,2
			3,1
			2,5

Решение: Фактический коэффициент запаса определим по формуле  где  Подставляя числовые значения, получаем

  ЗАДАНИЕ N 8 сообщить об ошибке Тема: Чистый сдвиг. Расчет на сдвиг (срез) Закон Гука при чистом сдвиге – это … 

			линейная зависимость между касательным напряжением и углом сдвига
			линейная зависимость между нормальным напряжением и продольной деформацией при линейном напряженном состоянии
			нелинейная зависимость между касательным напряжением и углом сдвига
			нелинейная зависимость между нормальным напряжением и продольной деформацией при линейном напряженном состоянии

Решение: При небольших напряжениях зависимость между касательным напряжением  и углом  при чистом сдвиге (см. рисунок) – линейная. Эта линейная зависимость и называется законом Гука при чистом сдвиге.

  ЗАДАНИЕ N 9 сообщить об ошибке Тема: Напряжения в поперечном сечении стержня при плоском изгибе Эпюра распределения касательных напряжений по высоте прямоугольного поперечного сечения балки показана на схеме …

			d
			b
			c
			a

Решение: Для балки прямоугольного поперечного сечения со сторонами b и h касательные напряжения определяются по формуле  Касательные напряжения по высоте сечения изменяются по закону квадратной параболой. Наибольшее напряжение имеет место при  Этим требованиям удовлетворяет схема d.

  ЗАДАНИЕ N 10 сообщить об ошибке Тема: Расчет балок на прочность Две балки одинакового поперечного сечения изготовлены из одного материала и нагружены равномерно распределенной нагрузкой с интенсивностью q. Балки будут равнопрочны, когда длина консоли  равна _____. Влиянием касательных напряжений пренебречь.

Решение: Балки будут равнопрочны, если максимальные нормальные напряжения в балках одинаковы. Из условий, что балки изготовлены из одного материала и имеют одинаковые поперечные сечения, следует, что максимальные изгибающие моменты в равнопрочных балках должны быть одинаковы. Для первой схемы нагружения  для второй –  Следовательно, балки будут равнопрочны при 

  ЗАДАНИЕ N 11 сообщить об ошибке Тема: Поперечная сила, изгибающий момент и их эпюры На схеме показана отсечная часть стержня и нагрузка, действующая на нее. Неверным является утверждение, что изгибающий момент …

			на участке CD меняется по линейному закону
			в сечении А равен нулю
			в сечении В изменяется скачком
			на участке АВ переменный

Решение: При изгибе выполняются дифференциальные зависимости где q – интенсивность распределенной нагрузки на участке;  – поперечная сила;  – изгибающий момент. Из анализа формул видно, что на участке, где к балке приложена равномерно распределенная нагрузка, поперечная сила меняется по линейному закону, а изгибающий момент по закону квадратной параболы. Следовательно, утверждение, что изгибающий момент на участке CD меняется по линейному закону будет неверным.

  ЗАДАНИЕ N 12 сообщить об ошибке Тема: Перемещения при изгибе. Расчет балок на жесткость Консольная балка длиной l нагружена равномерно распределенной нагрузкой интенсивностью q. Модуль упругости материала Е. Сечение круглое диаметромd. Радиус кривизны оси балки  в опасном сечении равен …

Решение: Кривизна оси стержня в сечении связана с изгибающим моментом, действующим в этом сечении, и жесткостью поперечного сечения на изгиб, в этом же сечении, зависимостью  Опасное сечение расположено вблизи заделки и  Для круглого сечения  После преобразований получим 

  ЗАДАНИЕ N 13 сообщить об ошибке Тема: Испытание конструкционных материалов на растяжение и сжатие Вид образца из пластичного материала после испытаний на сжатие показан на рисунке …

			d
			a
			b
			c

Решение: Образец из пластичного материала при испытании на сжатие не разрушается, а только расплющивается, что и показано на рисунке «d».

  ЗАДАНИЕ N 14 сообщить об ошибке Тема: Расчеты стержней на прочность и жесткость Элемент КСD закреплен с помощью шарнирно неподвижной опоры и стержня с жесткостью поперечного сечения на растяжение ЕА (см. рисунок). Система нагружена равномерно распределенной нагрузкой с интенсивностью q. Допустимая величина удлинения стержня  задана. Условие жесткости имеет вид …

Решение: Рассмотрим равновесие элемента КСD и определим продольную силу в стержне  Удлинение стержня  а условие жесткости имеет вид 

  ЗАДАНИЕ N 15 сообщить об ошибке Тема: Продольная сила. Напряжения и деформации Внутренний силовой фактор в сечении С-С стержня 1 равен …

Решение: Рассекаем стержень 1 сечением С-С и делим конструкцию на две части. Рассмотрим равновесие левой части конструкции (см. рисунок). Стержень 1 работает на растяжение. Составляем уравнение равновесия:  откуда продольная сила 

  ЗАДАНИЕ N 16 сообщить об ошибке Тема: Механические свойства и механические характеристики материалов На рисунке показана диаграмма растяжения образца диаметром 0,01 м. Масштаб нагрузки – 1 деление – 0,007 МН.  Предел прочности материала равен ___ МПа.

			446
			112
			357
			268

Решение: Предел прочности − это напряжение, соответствующее максимальной нагрузке, которую может выдержать образец. Предел прочности определяется по формуле  где А – первоначальная площадь поперечного сечения образца. В данном случае