ный граф. Число его вершин равно размерности матрицы n, i-й и j-и вершинам графа инцидентны δij ребер. Для неориентированного графа δij = δji и все его ребра определяются верхним правым треугольником матрицы, расположенным над диагональю, включая последнюю. Количество их равно сумме δij
nn
по этому треугольнику, т. е. P Pδij. Ребра ориентированного графа определяются всеми элементами
i=1 j=i
δij матрицы смежности. В обоих случаях по матрице смежности легко строится, например, список ребер, определяющий граф. Элементу матрицы смежности, расположенному в i-й строке и j-м столбце, соответствуют δij строк списка ребер (при δij = 0 — ни одной строки), в каждой из которых записаны номера i, j. Для неориентированного графа эти строки соответствуют только элементам описанного ранее верхнего правого треугольника матрицы смежности, т. е. элементам δij с j > i, а для ориентированного графа нужно рассматривать все элементы δij.
Маршруты, цепи и циклы
Определения
Пусть G — неориентированный граф. Маршрутом в G называется такая конечная или бесконечная последовательность ребер (. . . , e0, e1, . . . , en, . . .), что каждые два соседние ребра ei−1 и ei имеют общую инцидентную вершину. Одно и то же ребро может встречаться в маршруте несколько раз. В дальнейшем будут рассматриваться, в основном, конечные маршруты, т. е. конечные последовательности ребер (e1, e2, . . . , en). В таких маршрутах имеется первое ребро e1 и последнее ребро en. Вершина v0, инцидентная ребру e1 и не инцидентная e2, называется началом маршрута. Если же ребра e1 и e2 — кратные, необходимо специальное указание, какую из двух инцидентных им вершин считать началом маршрута. Аналогично определяется конец маршрута.
Вершины, инцидентные ребрам маршрута, кроме начальной и конечной, называются внутренни-
•Назад •Первая •Предыдущая •Следующая •Последняя •Перейти •Предметный указатель
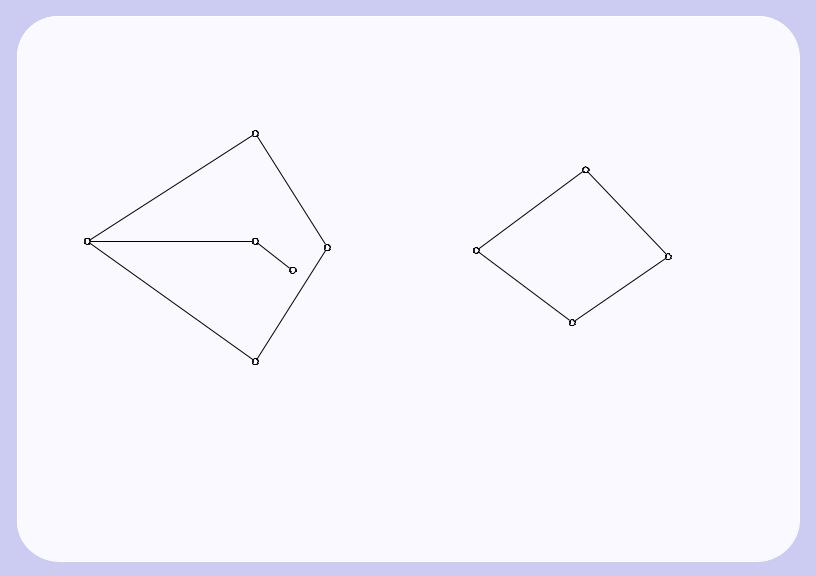
ми или промежуточными. Так как различные ребра маршрута могут быть инцидентными одной и той |
|||||
же вершине, начало или конец маршрута может одновременно оказаться и внутренней вершиной (см. |
|||||
маршрут (e1, e2, e3, e4, e5) на рис. 3.5). |
|
|
|||
|
|
v1 |
|
|
|
|
e1 |
|
e2 |
|
|
|
|
|
e1 |
e2 |
|
v0 = v4 |
|
|
|
||
e5 |
v5 |
|
|
|
|
|
|
v2 |
|
||
|
|
e6 |
v6 |
|
|
|
|
|
|
||
|
e4 |
|
e3 |
|
e |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
v3 |
|
|
Рис. 3.6. |
|
Рис. 3.5. |
|
|
|
|
Пусть маршрут M(e1, e2, . . . , en) имеет начало v0 и конец vn. Тогда его называют соединяющим вер- |
|||||
шины v0 и vn. Число ребер маршрута называется его длиной. Если v0 = vn, маршрут называют цикличе- |
|||||
ским. Отрезок (ei, ei+1, . . . , ej) конечного или бесконечного маршрута M сам является маршрутом. Он |
|||||
называется участком маршрута M. |
|
|
|
||
Маршрут M называется цепью, если каждое ребро встречается в нем не более одного раза, и про- |
|||||
стой цепью, если любая вершина графа G инцидентна не более чем двум его ребрам. Циклический |
|||||
|
•Назад •Первая •Предыдущая •Следующая •Последняя •Перейти •Предметный указатель |
||||
маршрут называют циклом, если он является цепью, и простым циклом, когда это простая цепь. Однако фактически циклом (соответственно, простым циклом) считают циклически упорядоченное множество ребер, в котором два соседних ребра имеют общую инцидентную вершину.
Участок цепи или цикла является цепью, а участок простой цепи или простого цикла — простой цепью.
Связные компоненты графа
Вершины v0, v00 G называются связанными, если существует маршрут M с началом v0 и концом v00. Легко видеть, что в этом случае существует также маршрут с началом v00 и концом v0. Для этого ребра маршрута M должны идти в противоположном порядке. Пусть вершина v G инцидентна более чем двум ребрам маршрута M, связывающего вершины v0 и v00, ei — первое из этих ребер, ej — последнее (j > i + 1). Тогда из маршрута M можно выбросить участок от (i + 1)-гo ребра до (i − 1)-го. Получится маршрут M0(e1, . . . , ei, ej, . . . , en). Если M0 — не простая цепь, то можно продолжать этот процесс выбрасывания его внутреннего участка. В конце концов получится простая цепь M , связывающая v0 и v00. Таким образом, связанные маршрутом вершины связаны также и простой цепью.
Если вершина v G связана с какой-либо другой вершиной v0, она связана и сама с собой. Пусть v и v0 связывает маршрут M(e1, e2, . . . , en), тогда v и v связывает маршрут M0(e1, e2, . . . , en, en−1, . . . , e2, e1), в котором сначала идут ребра маршрута M, а затем они же, но в обратном порядке. Однако обычно считают, что изолированная вершина также связана сама с собой и отношение связанности двух вершин, заданное на множестве вершин графа G, рефлексивно. Как было указано ранее, оно симметрично. Наконец, оно транзитивно. Если вершина v0 связана с вершиной v00 маршрутом M0(e01, . . . , e0n), а v00 с v000 —
маршрутом M00(e001, . . . , e00p) то v0 связана с v000 маршрутом M(e01, e02, . . . , e0n, e001, . . . , e00p), в которых сначала идут ребра маршрута M0, а затем ребра маршрута M00. Последовательность ребер M — это маршрут.
Действительно, кроме пары ребер e0n, e001, остальные пары соседних ребер являются соседними в одном из маршрутов M0 или M00 и имеют общую инцидентную вершину. Ребра же e0n и e001 инцидентны вершине
•Назад •Первая •Предыдущая •Следующая •Последняя •Перейти •Предметный указатель
v00.
Итак, отношение связанности вершин обладает свойствами отношения эквивалентности и определяет разбиение множества вершин графа на непересекающиеся подмножества Vi, Вершины одного и того же множества Vi связаны друг с другом, а вершины различных множеств Vi и Vj не связаны между собой. Поэтому в графе G нет ребер с концами в разных множествах Vi и Vj и он может быть разложен в прямую сумму подграфов: G = SG(Vj).
Граф G называется связным, если все его вершины связаны между собой. Поэтому все подграфы G(Vj) связны и называются связными компонентами рассматриваемого графа.
Расстояния
Пусть G — связный неориентированный граф, v0 и v00 — любые две его вершины. Тогда существует связывающая их простая цепь M(e1, e2, . . . , eq). Если количество q ребер этой цепи — не минимальное из возможных, то существует цепь M0(e1, e2, . . . , eq) связывающая v0и v00 и имеющая меньшее число ребер. Если и M0 не минимально, можно найти связывающую v0 и v00 цепь с еще меньшим количеством ребер и т. д. Однако этот процесс уменьшения числа ребер можно повторить не более q раз, так как это число каждый раз уменьшается не меньше чем на единицу. Поэтому существует связывающая v0 и v00 цепь
˜ с минимальным количеством ребер . Минимальная длина простой цепи с началом 0 и
M(˜e1, e˜2, . . . , e˜p) p v
концом v00 называется расстоянием d(v0, v00) между этими вершинами.
Считая каждую вершину v неориентированного графа связанной с самой собой, мы, по существу, ввели нулевые маршруты, не содержащие ребер, с началом и концом в любой вершине v G. В соответствии с этим расстояние d(v, v) между вершиной и ею самой равно 0. Для любой пары v0, v00 G различных вершин d(v0, v00) > 0, так как связывающая эти вершины цепь состоит хотя бы из одного ребра.
•Назад •Первая •Предыдущая •Следующая •Последняя •Перейти •Предметный указатель