Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Конотопский институт СумГУ

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

kontrolnye / Дискретка / Конспект лекций / graphs.pdf

Скачиваний:

Добавлен:

27.02.2016

Размер:

501.06 Кб

Скачать

☆

1 / 91 2 3 4 5 6 7 8 9 > Следующая >>>

Тема ¹ 3. Графы

Содержание

Основные понятия и операции	3
Графы, их вершины, ребра и дуги . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	3
Изображение графов . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	4
Матрица инцидентности и список ребер . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	6
Матрица смежности графа . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	9

Маршруты, цепи и циклы	10
Определения . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	10
Связные компоненты графа . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	12
Расстояния . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	13

Задача о кратчайшем пути	14
Постановка задачи . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	14
Нахождение кратчайшего пути в графе с ребрами единичной длины . . . . . . . . . . . . . . . .	15
Нахождение кратчайшего пути в графе c ребрами произвольной длины . . . . . . . . . . . . . .	19

Транспортные сети	22
Основные понятия . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	22
Задача о наибольшем потоке . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	25
Нахождение полного потока . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	27
Нахождение наибольшего потока . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	27

•Назад •Первая •Предыдущая •Следующая •Последняя •Перейти •Предметный указатель

Транспортная задача	30
Предметный указатель	39

•Назад •Первая •Предыдущая •Следующая •Последняя •Перейти •Предметный указатель

Основные понятия и операции

Графы, их вершины, ребра и дуги

Теорию графов начали разрабатывать для решения некоторых задач о геометрических конфигурациях, состоящих из точек и линий. В этих задачах несущественно, соединены ли точки конфигурации отрезками прямых или криволинейными дугами, какова длина линий и другие геометрические характеристики конфигурации. Важно лишь то, что каждая линия соединяет какие-либо две из заданных точек. Таким образом, можно дать определение графа как совокупности двух множеств V (точек) и E (линий), между элементами которых определено отношение инцидентности, причем каждый элемент e E инцидентен ровно двум элементам v0, v00 V . Элементы множества V называются вершинами графа G, элементы множества E — его ребрами. Вершины и ребра графа G называют еще его элементами и вместо v V, e E пишут соответственно v G и e G.

Внекоторых задачах инцидентные ребру вершины неравноправны, они рассматриваются в определенном порядке. Тогда каждому ребру можно приписать направление от первой из инцидентных вершин ко второй. Направленные ребра часто называют дугами, а содержащий их граф — ориентированным (граф, определенный ранее, называется неориентированным). Первая по порядку вершина, инцидентная ребру ориентированного графа, называется его началом, вторая — его концом. Говорят еще, что ребро ориентированного графа выходит из начала и входит в конец.

Вдальнейшем оказалось, что понятие графа можно применить не только при исследовании геометрических конфигураций.Особенно часто определяют графы при анализе функционирования систем. С отдельными компонентами изучаемой системы удобно связывать вершины графа, а с парами взаимодействующих компонент — его ребра. Построенный таким образом граф называют структурным графом системы..

•Назад •Первая •Предыдущая •Следующая •Последняя •Перейти •Предметный указатель

		в)
а)	б)	г)
	е)	ж)
д)		з)
	Рис. 3.1.
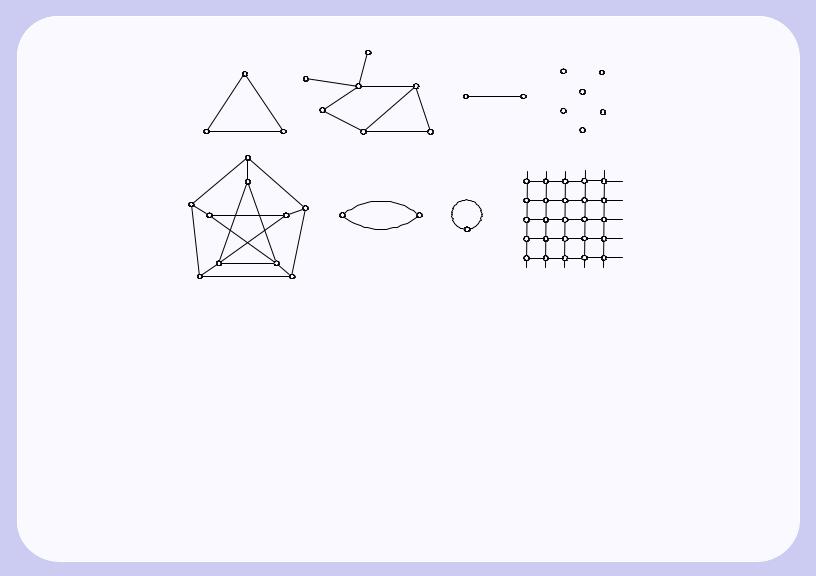
Изображение графов
На рис. 3.1,а–з изображены некоторые неориентированные графы. Множество ребер E может быть
пустым (см. рис. 3.1,г). Если же множество вершин V пусто, то пусто и E. Такой граф называется
пустым. Линии, изображающие ребра графа, могут пересекаться, но точки пересечения не являют-
ся вершинами (см. рис. 3.1,д); различные ребра могут быть инцидентны одной и той же паре вершин
(рис. 3.1,е), в этом случае они называются кратными; граф, содержащий кратные ребра, часто называ-
ют мультиграфом. Ребро может соединять некоторую вершину саму с собой (рис. 3.1,ж), такое ребро
называется петлей. На рис. 3.1,з изображен фрагмент бесконечного графа. Его вершины — это точки
•Назад •Первая •Предыдущая •Следующая •Последняя •Перейти •Предметный указатель

плоскости с целыми координатами (x, y), а ребра — соединяющие их горизонтальные и вертикальные
отрезки длины 1.
Обычно рассматриваемые графы конечны, т. е. конечны множества их элементов (вершин и ребер).
Поэтому конечность этих графов не будет специально оговариваться. Однако некоторые понятия и
результаты, о которых будет идти речь, относятся к произвольным графам.
а)	б)	в)	г)

д)	е)	ж)	з)
	Рис. 3.2.
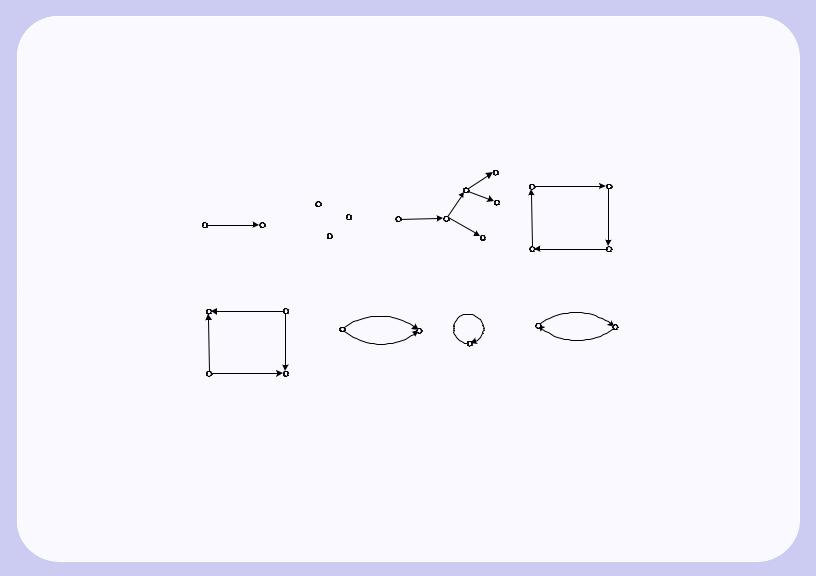
При изображении ориентированных графов (рис. 3.2,а–з) направления ребер отмечаются стрелка-
ми, примыкающими к их концам. Ориентированный граф также может иметь кратные ребра (рис. 3.2,е),
петли (рис. 3.2,ж), а также соединяющие одни и те же вершины ребра, идущие в противоположных на-
правлениях (рис. 3.2,з).
Каждому неориентированному графу можно поставить в соответствие ориентированный граф с тем
•Назад •Первая •Предыдущая •Следующая •Последняя •Перейти •Предметный указатель

же множеством вершин, в котором каждое ребро заменено двумя ориентированными ребрами, инци-
дентными тем же вершинам и имеющими противоположные направления. Такое соответствие будем
называть каноническим.
Матрица инцидентности и список ребер
Задать граф — значит описать множества его			VII
вершин и ребер, а также отношение инцидент-			VII
вершин и ребер, а также отношение инцидент-
ности. Когда граф G — конечный, для описа-		9
ния его вершин и ребер достаточно их за-	V	9		10	VI
нумеровать. Пусть v1v2, . . . , vn — вершины графа	V				VI
G; e1e2, . . . , em — его ребра. Отношение инцидент-
ности можно определить матрицей \|\|εij\|\|, имею-		7		8
щей m строк и n столбцов. Столбцы соответству-
ют вершинам графа, строки — ребрам. Если ребро			6
ei инцидентно вершине Vj, то εij = 1, в противном	4	III	6	IV	5
случае εij = 0. Это так называемая матрица ин-	4	III		IV	5
случае εij = 0. Это так называемая матрица ин-
цидентности неориентированного графа G, ко-		2		3
торая является одним из способов его определе-		2		3
торая является одним из способов его определе-
ния (для графа на рис. 3.3 она дана в табл. 3.1,a).			1
	I		1		II
	I				II
			Рис. 3.3.
•Назад •Первая •Предыдущая •Следующая •Последняя •Перейти •Предметный указатель

Таблица 3.1.

			а)												б)
	I	II	III	IV		V	VI	VII			I		II	III	IV	V VI		VII
	I	II	III	IV		V	VI	VII			I		II	III	IV	V VI		VII

1	1	1	0	0		0	0	0		1	-1 1 0				0	0	0	0
2	1	0	1	0		0	0	0	2		-1 0 1				0	0	0	0
3	0	1	0	1		0	0	0	3		0 -1 0				1	0	0	0
4	1	0	0	0		1	0	0	4		0 0 -1 0 1 0							0
5	0	1	0	0		0	1	0	5		0 0 -1 0 0 1							0
6	0	0	1	1		0	0	0	6		0 0 -1				0	0	0	1
7	0	0	1	0		1	0	0	7		0	0		0	0	0	0	2
8	0	0	0	1		0	1	0
9	0	0	0	0		1	0	1
10	0	0	0	0		0	1	1
						в)								г)
			Рёбра		Вершины					Рёбра			Вершины
			Рёбра		Вершины					Рёбра			Вершины

			1			I,		II			1			I,		II
			2			I,		III			2			I,		III
			3			II,		IV			3			II,		IV
			4			I,		V			4			III,		V
			5			II,		VI			5			II,		VI
			6			III,		IV			6			III,		VII
			7			III,		V			7			VII,		VII
			8			IV,		VI
			9			V,		VII
			10			VI,		VII

•Назад •Первая •Предыдущая •Следующая •Последняя •Перейти •Предметный указатель

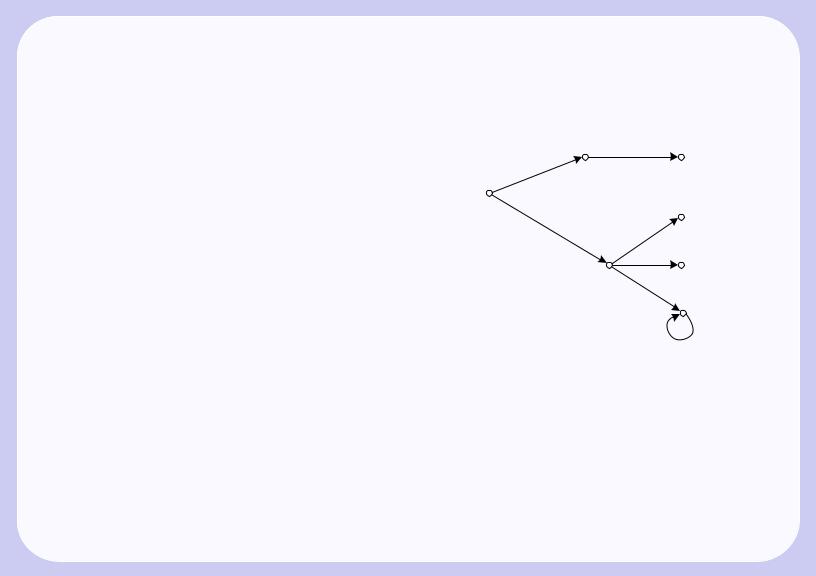
В матрице инцидентности \|\|εij\|\| ориентированного графа G, если вершина Vj — начало ребра ai, то
εij = −1; если vj — конец ai, то εij = 1; если ai — петля, а vj — инцидентная ей вершина, то εij = a, где
α — любое число,отличное от 1, 0 и −1, в остальных случаях εij = 0 (пример — табл. 3.1,б для графа на
рис. 3.4).
В каждой строке матрицы инцидентности для	II	3	IV
неориентированного или ориентированного гра-	II	3	IV
фа только два элемента отличны от 0 (или один,	1
если ребро является петлей). Поэтому такой спо-	I
соб задания графа εij оказывается недостаточно	I		V
соб задания графа εij оказывается недостаточно			V
экономным. Отношение инцидентности можно	2	4
еще задать списком ребер графа. Каждая строка	2	4
еще задать списком ребер графа. Каждая строка		5	VI
этого списка соответствует ребру, в ней записаны		5	VI
номера вершин, инцидентных ему. Для неориен-	III	6
тированного графа порядок этих вершин в строке			VII
произволен, для ориентированного первым стоит		7	VII
номер или другое наименование начала ребра, а
вторым — его конца. В табл. 3.1,в и табл. 3.1,г при-
водятся списки ребер для графов, изображенных	Рис. 3.4.
на рис. 3.3 и 3.4.	Рис. 3.4.
на рис. 3.3 и 3.4.
По списку ребер графа легко построить его матрицу инцидентности. Действительно, каждая строка
этого списка соответствует строке матрицы с тем же номером. Для неориентированного графа в строке
списка указаны номера элементов строки матрицы инцидентности, равные 1, и для ориентированно-
го графа в этой строке первым стоит номер элемента строки матрицы, равного −1, а вторым — номер
элемента, равного +1.
•Назад •Первая •Предыдущая •Следующая •Последняя •Перейти •Предметный указатель

1 / 91 2 3 4 5 6 7 8 9 > Следующая >>>

Соседние файлы в папке Конспект лекций

#
27.02.2016289.96 Кб37automatons.pdf
#
27.02.2016501.06 Кб39graphs.pdf
#
27.02.2016265.84 Кб47logic.pdf
#
27.02.2016151.77 Кб16sets.pdf

Основные понятия и операции

Графы, их вершины, ребра и дуги

Изображение графов

Матрица инцидентности и список ребер