§ 5. Незалежні випробування. Схема та формула Бернуллі, їх узагальнення
У багатьох задачах теорії ймовірностей, статистики та практики доводиться досліджувати серії п випробувань в однакових умовах, причому ймовірність появи події А в усіх випробуваннях однакова і не залежить від появи або не появи події А в інших випробуваннях. Таку послідовність незалежних випробувань називають схемою Бернуллі.
Наприклад, схемою Бернуллі є п підкидань однієї і тієї ж монети. Ймовірність появи герба дорівнює 0,5, а ймовірність його не появи (поява цифри) також буде 0,5.
Нехай випадкова подія А може з'явитися у кожному випробуванні з ймовірністю Р(А) = р або не з'явитися з ймовірністю q = Р(А)=1-р. Треба знайти ймовірність того, що при п випробуваннях подія А з'явиться т разів. Шукану ймовірність позначимо Рп(т).
Спочатку розглянемо появу події А три рази в чотирьох випробуваннях. Тоді можливі такі події
Формулу (17) називають формулою Бернуллі. Приклад 10.10. Яка ймовірність того, що при 10 киданнях монети герб випаде 5 разів?
Розв'язання. У цьому прикладі ймовірність випадання
Одержаний результат дещо несподіваний, оскільки очікуваний результат має бути близьким до 0,5, бо 5 - це половина всіх кидань. Виявляється, що умова: герб повинен випасти рівно 5 разів - досить жорстка, тому і ймовірність її невелика.
Приклад 10.11. Яка ймовірність того, що при 12000 кидань монети герб випаде 6000 разів?
Обчислити це число складно.
Для великих п і т французький математик Лаплас (1749-1827) знайшов наближену формулу
Формулу (18) приймаємо без доведення. Відзначимо, що її можна отримати з формули (17) шляхом граничного переходу
що і у прикладі 10.10. Вимога, щоб при 12000 киданнях монети герб випав рівно 6000 разів, дуже жорстка, а тому і ймовірність такої події мала.
Зовсім інший результат маємо, якщо у схемі Бернуллі поставити задачу: знайти ймовірність того, що в серії пвипробувань подія А з'явиться не менше т] разів і не більше т2 разів. Цю ймовірність позначають Рn(m1, т2).
Лаплас показав, що має місце наближена формула
Складені таблиці значень функції Ф(х) для значень х з відрізку [0; 5] (див. Додаток 3). Для х>5 значення Ф(х)=0,5.
Приклад 10.12. Яка ймовірність того, що при 12000 киданнях монети герб випаде не менше 6000 разів і не більше 6300 разів?
Одержаний результат добре узгоджується з статистичними результатами частоти появи герба при великій кількості кидань монети.
Приклад 10.13. При виробництві деякої масової продукції ймовірність появи браку дорівнює 0,01. Яка ймовірність того, що в партії із 100 виробів цієї продукції 2 вироби будуть з боком?
Перші два результати відрізняються на 0,001, третій відрізняється від перших двох на 0,058, тобто значно більше. Причина такого значного відхилення в тому, що n = 100, т=2 для формули Лапласа малі.
§ 6. Випадкові величини
6.1. Закон розподілу випадкової величини
При дослідженнях виникають такі випадкові події, наслідком яких є поява деякого числа, заздалегідь невідомого. Тому такі числові значення є випадковими. Наприклад, кількість очок, які випадають при киданні грального кубика; кількість студентів, які прийдуть на деяку лекцію; кількість цукрових буряків, яку чекають одержати з кожного гектара тощо.
Означення 10.16. Випадковою називають таку величину, яка внаслідок випробування може прийняти лише одне числове значення, заздалегідь невідоме і обумовлене випадковими причинами. При цьому, якщо випадкова величина приймає відокремлені, ізольовані одне від одного числові значення, які можна занумерувати, то її називають дискретною випадковою величиною.
Якщо ж випадкова величина може прийняти будь-яке числове значення з деякого проміжку <а;Ь>, то її називають неперервною випадковою величиною.
Наприклад, кількість влучень у мішень при трьох пострілах є дискретна випадкова величина, оскільки вона може приймати лише чотири ізольовані значення: 0, 1,2, 3.
Величина похибки при вимірюванні певної відстані, розміри деталі, які виготовляє станок-автомат є прикладами неперервної випадкової величини.
Означення 10.17. Законом розподілу випадкової величини називають співвідношення, яке встановлює зв'язок між: можливими значеннями випадкової величини і відповідними їм ймовірностями.
Закон розподілу дискретної випадкової величини задають таблицею, у верхньому рядку якої виписані всі можливі значення де,, х2, х3, ..., хп величини Дав нижньому рядку виписані ймовірності рх, р2, р3, ..., рп значеньX. Таблиця читається так: випадкова величина X може приймати значення х, з імовірністю
Оскільки в результаті випробувань величина X завжди приймає одне із значень хх, х2, х3, ..., хп , то рх + р2 +... + рn = 1.
Приклад 10.14. В грошовій лотереї розігруються 1 виграш у 1000 гривень, 10 виграшів по 100 гривень і 100 виграшів по 1 гривні при загальній кількості білетів 10000. Знайти закон розподілу випадкового виграшу X для власника одного лотерейного білета.
Розв'язання. Очевидно, можливими значеннями для X є х,=0, x2=1, х3=100, х4=1000. Їх ймовірності р2=0.01, р3 =0,001, р4 =0,0001, р1 =1-0,01-0,001-0,0001 = 0,9889 . Тому закон розподілу виграшу X можна задати таблицею
Для неперервної випадкової величини не можна побудувати таблицю розподілу цієї величини. Тому неперервні випадкові величини вивчаються іншим способом.
Нехай X є неперервною випадковою величиною з можливими значеннями з деякого інтервалу (а; Ь) і х - дійсне число. Запис X < х означає подію: випадкова величина X прийняла значення, менше х. Ймовірність цієї події Р(Х < х) є деяка функція х: F(x) = Р(Х < х).
Означення 10.18. Інтегральною функцією розподілу або інтегральним законом розподілу неперервної випадкової величини X називається функція
F(x) = P(X<x).
Зауважимо, що інтегральна функція розподілу F(x) визначається так само і для дискретних випадкових величин.
Теорема 10.11. Інтегральна функція розподілу неперервної випадкової величини X має такі властивості:
Доведення. Перша властивість F(x) випливає з того, що F(x) є ймовірність.
Нехай хх <х2. Тоді подію: X прийме значення, менше х2, можна представити як суму двох несумісних подій: X прийме значення, менше хх і Сприйме значення з проміжку [хх;х2). За теоремою про ймовірність суми двох несумісних подій маємо:
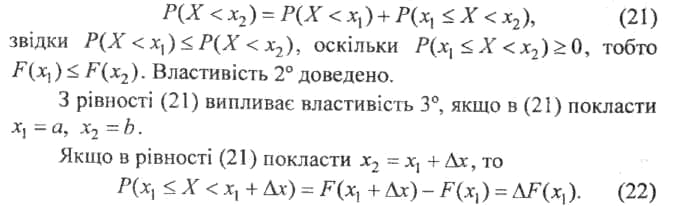
Зокрема, якщо можливі значення неперервної випадкової величини X розміщені на всій числовій осі, то
