§ 3. Теореми про ймовірність події

Вважатимемо, що всі події, про які йтиме мова в наступних теоремах, допустимі відносно деякої повної системи рівноможливих подій.

Теорема 10.1. Імовірність Р(А) коленої події А задовольняє нерівності 0 < Р(А) < 1, причому Р(О) = 0, Р(І) = 1.

Доведення. Нехай п - кількість усіх можливих випадків, а k - кількість випадків, що сприяють події А. Тоді 0 < к < п, звідки, за означенням 10.12, , причому для неможливої події О число k = 0, а для вірогідної події I число k = п. Теорему доведено.

Теорема 10.2. Імовірність суми двох несумісних подій А і В дорівнює сумі їх імовірностей, тобто, якщо А·В=О, то

Доведення. Нехай п - кількість усіх можливих випадків, к_х -кількість випадків, що сприяють події А, к₂ - кількість випадків, що сприяють події В. Оскільки події А і В несумісні, то кожний випадок, що сприяє одній з подій, не сприяє іншій. Але кожний випадок, який сприяє події А або події В, сприяє також і події А + В і навпаки, кожний випадок, що сприяє події А + В, сприяє події А або події В. Тому кількість випадків, що сприяють події А + В, дорівнює к_х + к₂. За означенням 10.12 імовірності маємо

Теорему доведено.

Теорема 10.2 узагальнюється на випадок довільного скінченного числа попарно несумісних подій А_і (і = 1, п):

Рівність (3) доводиться методом повної математичної індукції на основі рівності (2).

Теорема 10.3. Імовірність суми двох довільних подій А і В обчислюється за формулою

Доведення. Безпосередньо перевіркою встановлюємо, що

причому події АВ і АВ, та АВ і АВ несумісні, оскільки

Події АВ,АВ, А В попарно несумісні. Це випливає з обчислення

Додамо почленно рівності (5). Отримаємо

Звідси за формулами (3) і (5)

Теорему доведено.

Теорема 10.4. Для довільної події А маємо рівність

Доведення. Подія А + А= І, причому події А і А несумісні, тому за теоремами 10.2 і 10.1 маємо

звідки і випливає рівність (6). Теорему доведено.

Приклад 10.4. У партії з 15 деталей 12 стандартних. З цієї партії навмання взято 2 деталі. Яка ймовірність того, що хоч одна з цих двох деталей стандартна?

Розв'язання. Позначимо А подію: з двох вибраних деталей одна (точно одна) стандартна, а В подію: обидві вибрані деталі стандартні. Тоді подія А + В - хоч одна з двох вибраних деталей стандартна. Події А і В, очевидно, несумісні, тому за теоремою 10.2 Р(А + B) = Р(А) + Р(В). Але

Приклад 10.5. Кинуто два гральних кубика. Яка ймовірність того, що хоч на одному з них випаде трійка?

Розв'язання. Нехай подія А: на першому гральному кубику випала трійка, подія В: на другому гральному кубику випала трійка. Тоді подія АВ: на обох гральних кубиках випала трійка, а подія А + В: хоч на одному гральному кубику випала трійка. За теоремою 10.3 маємо Р(А + В) = Р(А) + Р(В) - Р(АВ).

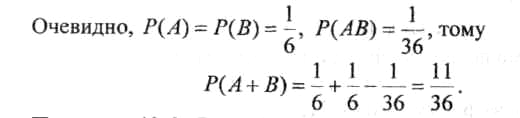
Приклад 10.6. В урні 16 кульок, з них 4 білих, а інші кольорові. Вийняли 3 кульки. Яка ймовірність того, що серед них є хоч одна кольорова?

Розв'язання. Нехай подія А: серед вийнятих кульок є хоч одна кольорова, тоді подія А: всі три вийняті кульки білі.