Тема 5 Основные законы распределения дискретных случайных величин. Формула Бернулли
Вопросы для самостоятельного изучения
1. Формула Бернулли.
Пример 1. Устройство состоит из 8 независимо работающих элементов. Вероятность отказа каждого элемента за время Т одинаковы и равны 0,2. Найти вероятность того, что из 8 откажут 2 элемента.
Решение. В данном случае событие А – отказ прибора, n = 8, m=2, р = р(А) = 0,2, следовательно q=1-р=0,8.По формуле Бернулли находим вероятность
Пример 2. Для нормальной работы автобазы на линии должно быть не менее восьми машин, а их имеется десять. Вероятность невыхода каждой автомашины на линию равна 0,1. Найти вероятность нормальной работы автобазы на ближайший день.
Решение. Событие А – выход автомашины на линию. В нашем случае n = 10, m = 8,9,10; q q = р(А) = 0,1; р = р(А) = 1-q = 0,9.
Автобаза будет работать нормально, если на линию выйдут или восемь (событие В), или девять (событие С), или десять автомашин (событие Д). По теореме сложения для несовместных событий имеет
р(F)
= р(В+С+D)
=
Каждое слагаемое находим по формуле Бернулли. В результате получим:
Р(F)
=
Пример 3. Вероятность хотя бы одного попадания в мишень при трех выстрелах равна 0,936. Найти вероятность того, что из шести выстрелов стрелок попадет в мишень пять раз. (Предполагается, что вероятность попадания при каждом выстреле одна и та же)
Решение. Событие
А – попадание в мишень при одном выстреле,
В – хотя бы одно попадание при трех
выстрелах. По условию задачи
=3,n=6,
n=5,
р(В)=0,936. Требуется найти
.
Для определения вероятности попадания
при одном выстреле р(А)=1-q
используем теорему о «вероятности
появления хотя бы одного события n
независимых событий», которая в нашем
случае запишется:
Р(В)=1-
=1-
=0.936
Отсюда
=
1-0,936=0,064;q
=
=0,4
Следовательно, р = 1-0,4=0,6. Для нахождения искомой вероятности применим формулу Бернулли:
Рекомендуемая литература
1. Вентцель Е.С. Теория вероятностей. Учебник. Издание восьмое, стереотипное. – М.: Высшая школа, 2002 г. - 575 с.
2. Вентцель Е.С., Овчаров Л.А.. Теория вероятностей и её инженерные приложения. Учебное пособие. Издание третье, переработанное и дополненное. – М.: «Академия», 2003 г. – 464 с.
3. Гмурман В.Е. Теория вероятностей и математическая статистика. Учебное пособие. Издание десятое, стереотипное. - М.: Высшая школа», 2004 г. – 480 с.
Тема № 6 Основные законы распределения дискретных случайных величин. Локальная теорема Муавра-Лапласа, формула Пуассона
Вопросы для самостоятельного изучения
1. Локальная теорема Лапласа.
Пример 1. Вероятность изготовления детали высшего сорта на данном станке рана 0,4. найти вероятность того, что среди наудачу взятых 25 деталей половина окажется высшего сорта.
Решение.
Событие А – деталь высшего сорта. По
условию задачи n
=25,m=13?
р=р(А)=0,4, q-0,6.
Требуется найти
.
Воспользуемся локальной формулой
Лапласа:
=
.
X
=
.
По таблице
(приложение 1) находим
(1,04)=0,2323
Искомая вероятность:
=
2. Наивероятнейшее число наступлений события (наивероятнейшая частота)
Решение. Событие А - изделие высшего сорта. Известие, что р=0,31, п= 75, q=1-p-0.69. Составляем двойное неравенство:
.
.
Рекомендуемая литература
1. Вентцель Е.С. Теория вероятностей. Учебник. Издание восьмое, стереотипное. – М.: Высшая школа, 2002 г. - 575 с.
2. Вентцель Е.С., Овчаров Л.А.. Теория вероятностей и её инженерные приложения. Учебное пособие. Издание третье, переработанное и дополненное. – М.: «Академия», 2003 г. – 464 с.
3. Гмурман В.Е. Теория вероятностей и математическая статистика. Учебное пособие. Издание десятое, стереотипное. - М.: Высшая школа», 2004 г. – 480 с.
Тема № 7 Основные законы распределения дискретных случайных величин. Интегральная теорема Лапласа
Вопросы для самостоятельного изучения
1. Интегральная теорема Лапласа.
Пример 1. Вероятность выигрыша на один билет равна 0,1. Какова вероятность того, что из 60 билетов выигрышных окажется то 5 до 10 билетов.
Решение.
Событие А – выигрышный билет. По условию
задачи n=60,
а=5,
в=10,
р=0,2, q=0,8.
Требуется найти
.
Применяем интегральную теорему Лапласа.
Находим
;
.
Искомая вероятность равна:
Пример 2. Вероятность попадания в мишень равна 0,8. Стрелок делает 100 выстрелов. Найти а) наивероятнейшее число попадания и вероятность этого числа; б) вероятность того, что число попаданий будет не менее (по крайней мере, хотя бы) 75.
Решение.
Событие А – попадание в мишень. По
условию задачи n-100,
а=75,
в=100.
Надо найти
.
А) Наивероятнейшее число находим из неравенства:
Для вычисления
вероятности
воспользуемся локальной формулой
Лапласа:
где
Находим
=0,3989.
Искомая вероятность:
.
Б) Вероятность
определяем
по интегральной формуле Лапласа:
;
.
.
Пример 3. Вероятность того, что деталь стандартна, равна 0,9. Найти вероятность того, что среди случайно отобранных 400 деталей относительная частота появления стандартных изделий отклонится от вероятности р=0,9 по абсолютной величине не более, чем на 0,03.
Решение.
Событие А – стандартное изделие. По
условию задачи р=0,9; q=0,1;
n=400;
.
Требуется найти вероятность
Воспользуемся следствием интегральной теоремы Лапласа:
.
Имеем:
Задания для самостоятельной работы
1) Вероятность того, что из двух приобретенных билетов оба окажутся выигрышными рана 0,49. Определить вероятность того, что из шести билетов выиграют три.
2) Вероятность прокола колеса автомобиля при поездке равна 0,1. На сколько вероятнее доехать до конечного пункта следования с запасным колесом, чем без запасного колеса?
3) Игральная кость бросается 120 раз. Определить наивероятнейшее число выпадений шести очков на верхней грани кости.
4) На складе находится продукция двух цехов, причем в продукции плюс первого цеха содержится 60 % изделий высшего сорта, в продукции второго цеха – 70%. Для контроля качества продукции берутся 50 продукций первого цеха и 40 изделий второго цеха. Определить, в продукции какого цеха наивероятнейшее число изделий высшего сорта окажется наибольшим.
5) В зимнее время вероятность своевременного прибытия поезда на станцию принимается равным 0,8. Определить вероятность того, что из 30 ожидаемых поездов 25 прибудут своевременно.
6) На факультете института 40% всех студентов занимаются в спортивных секциях. Найти наивероятнейшее число студентов, занимающихся в спортивных секциях, их 250 студентов и вероятность того, что именно это число студентов занимается в спортивных секциях.
7) Школьники посадили на своем участке 500 деревьев. Вероятность того, что дерево приживется равна 0,6. Определить вероятность того, что число прижившихся деревьев окажется в пределах от 278 до333.
8) Известно, что для присуждения спортивных разрядов по стрельбе необходимо набрать хотя бы 90 очков из 100 возможных. Определить вероятность того, что стрелок станет разрядником, если для него вероятность попадания в цель при каждом выстреле равна 0,8.
9) При массовом выпуске некоторой продукции бывает в среднем 4 % брака. Определить вероятность того, что в партии 625 единиц этой продукции отклонение от установленного процента брака по абсолютной величине будет не более чем 0,02.
10) Вероятность безбилетного проезда на транспорте равна 0,05. Обследовано 400 человек. С вероятностью 0,9545 определить:
а)границы изменения относительной частоты безбилетных пассажиров;
б)границы, в которых заключено число безбилетных пассажиров среди обследованных.
11) Всхожесть семян характеризуется вероятностью 0,7. Определить, сколько нужно посеять семян, чтобы с вероятностью 0,9973 можно было утверждать, что частность проросших семян будет отличатся от 0,7 по абсолютной величине не более, чем на 0,02.
Рекомендуемая литература
1. Вентцель Е.С. Теория вероятностей. Учебник. Издание восьмое, стереотипное. – М.: Высшая школа, 2002 г. - 575 с.
2. Вентцель Е.С., Овчаров Л.А.. Теория вероятностей и её инженерные приложения. Учебное пособие. Издание третье, переработанное и дополненное. – М.: «Академия», 2003 г. – 464 с.
3. Гмурман В.Е. Теория вероятностей и математическая статистика. Учебное пособие. Издание десятое, стереотипное. - М.: Высшая школа», 2004 г. – 480 с.
Тема № 8 Определение дискретной случайной величины и её законы распределения
Вопросы для самостоятельного изучения
1. Дискретная (прерывная) случайная величина.
Пример 1. В некотором цехе изделия второго сорта составляют 10% всех изделий. Составить закон распределения числа изделий второго сорта из взятых неудачу трех изделий. Вычислить числовые характеристики случайной величины Х – числа изделий второго сорта.
Решение. Пусть Х – число изделий второго сорта (т.е. число наступления события). Тогда вероятность появления изделия второго сорта в одном отдельно взятом испытании р=0,1, q=1-р=0,9. Наименьшее значение, которое может принимать случайная величина Х равно нулю, т.е. среди трех наудачу взятых изделий нет изделия второго сорта. Далее будут значения х=1, х=2, х=3. А вероятности при составлении закона распределения вычисляются с использованием формулы Бернулли.
;
_____________
Закон распределения случайной величины Х будет иметь вид
|
Х |
0 |
1 |
2 |
3 |
|
Р |
0,729 |
0,243 |
0,027 |
0,001 |
Вычислим числовые характеристики случайной величины Х.
Математическое ожидание:
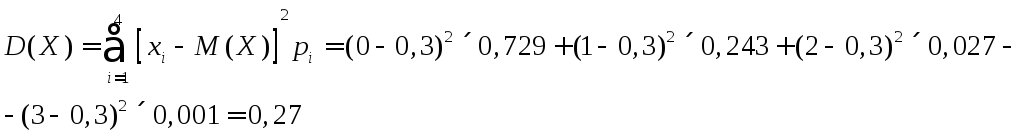
или, используя упрощенную формулу дисперсии, вычислим:
Пример 2. Стрелок стреляет в тире на приз за попадание. Вероятность попадания при каждом выстреле равна 0,3. Разрешается сделать не более четырех выстрелов. Стрелок получает приз после первого же попадания. Составить закон распределения числа выстрелов, в результате которых стрелок может получить приз.
Решение.
Пусть Х – число выстрелов (т.е. число
испытаний), в результате которых стрелок
может получить приз. Случайная величина
Х принимает значение 1, 2, 3, 4. Вероятности
при составлении закона распределения
будем вычислять с применением теорем
сложения и умножения вероятностей.
Сделав один выстрел, стрелок сразу же
получает приз, если он попал, следовательно,
.
Если сделал два выстрела, стрелок
получает приз, то это означает, что после
первого выстрела стрелок промахнулся,
а вторым выстрелом он поразил мишень,
следовательно,
и т.д. При четырех выстрелах возможны
две комбинации: стрелок три раза
промахнулся и последний четвертый раз
попал или четыре раза промахнулся:
.
-
X
P
1
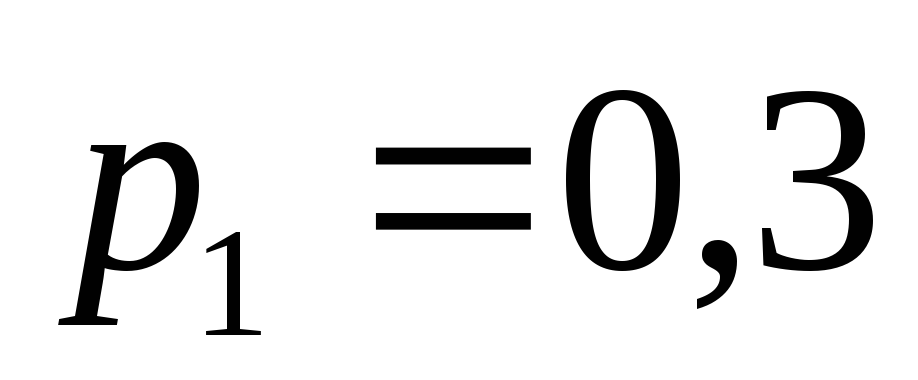
2
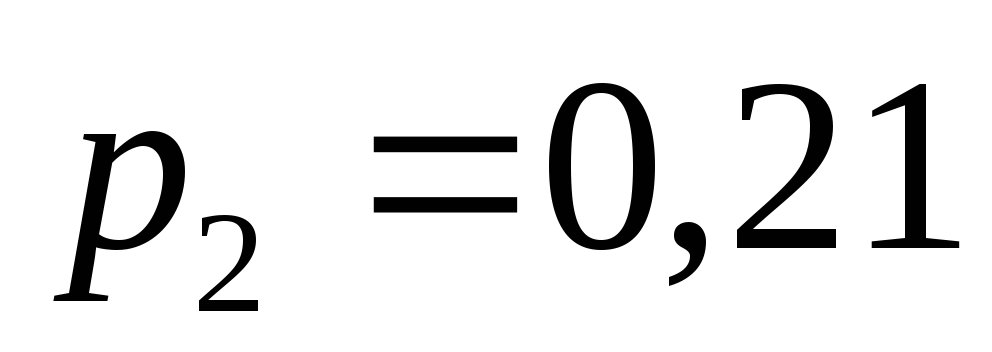
3
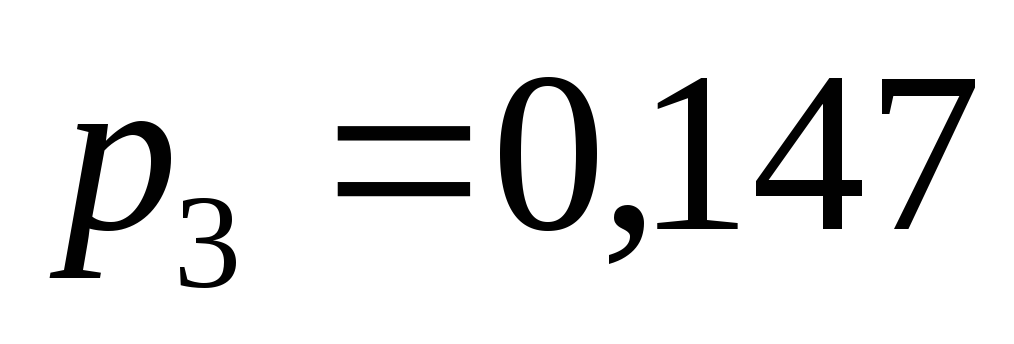
4
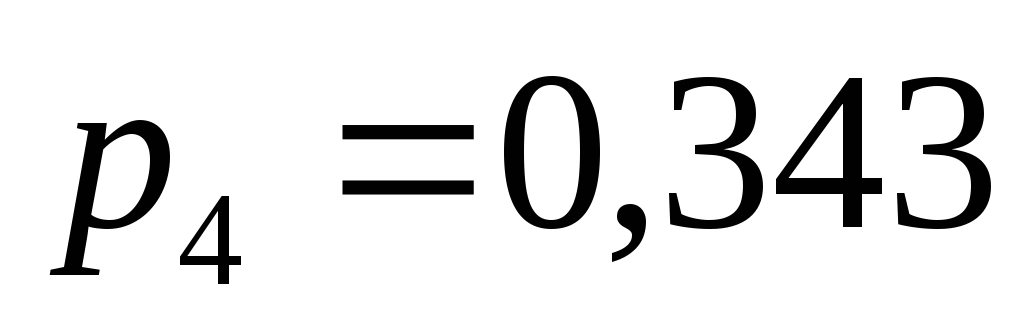
Вычислим числовые характеристики случайной величины:
.
Рекомендуемая литература
Баврин И.И., Матросов В.Л. Высшая математика: Учебник для студентов высших учебных заведений. – М.: Гуманит. изд. центр ВЛАДОС, 2003 г. - 400 с.
Тема № 9 Числовые характеристики: математическое ожидание, дисперсия, среднеквадратическое отклонение
Вопросы для самостоятельного изучения
1. Теоремы о математическом ожидании и дисперсии числа появлений события в n независимых испытаниях.
Пример 1. Вероятность изготовления стандартной лампочки 0,85. Определить математическое ожидание и дисперсию числа стандартных лампочек, если партия ламп состоит из 500 штук.
Решение. Обозначим вероятность появления стандартной электрической лампочки р=0,85, тогда q=1-р=0,15. Исследовано n = 500 шт.
Найдём М (Х) = np
= 500
0,85
= 425;
D
(Х) = npq
=500
0,85
0,15=63,75
Ответ М (Х) = 425; D (x) = 63.75
Примечание: Если при составлении закона распределения Х – число наступлений события (вероятности рассчитывает по формуле Бернулли), то числовые характеристики можно вычислить по формулам:
М(Х)=np, D(Х) = npq
Тогда по данным
задачи №1: М(Х) = 3
0,1=0,3;
D(Х)
= 3
0,1
0,9=0,27
Задания для самостоятельной работы
1) Вероятность возникновения погрешности при изменении равна 0,2. Проведено три измерения. Составить закон распределения случайной величины – числа измерений произведенных без погрешности. Вычислить числовые характеристики: математическое ожидание М(Х), дисперсию D(Х).
2) Прибор укомплектовывается тремя однотипными блоками. Контролер проверяет последовательно каждый блок на работоспособность. Как только выявляется неработающий блок, прибор бракуется. Составить закон распределения случайной величины – числа проверяемых блоков приборов, если вероятность появления неисправного блока равна 0,1. Найти числовые характеристики: М(Х), D(X).
3) Четыре покупателя входят в магазин. Для каждого покупателя вероятность сделать покупку равна 0,6. составить закон распределения случайной величины - числа покупателей, сделавших покупку. Найти числовые характеристики случайной величины: М(Х), D(X).
4) На экзамене студенту задаются дополнительные вопросы, но не более трех. Как только студент правильно отвечает на заданный вопрос, экзаменатор прекращает задавать дополнительные вопросы. Вероятность того, что студент правильно ответит на любой заданный вопрос, равна 0,7. Составить закон распределения случайной величины – числа дополнительных вопросов, заданных студенту. Вычислить: М(Х), D(X).
5) Вероятность того, что телевизор не потребует ремонта в течении гарантированного срока равна 0,8. Составить закон распределения случайной величины – числа телевизоров, которые не потребуют гарантированного ремонта, из пяти проданных телевизоров. Найти числовые характеристики М(Х), D(X).
6) Даётся пять попыток включить двигатель до первой успешной попытки. Вероятность того, что двигатель включится равна 0,6. Составить закон распределения случайной величины – числа попыток, в результате которых можно запустить двигатель. Найти числовые характеристики: М(Х), D(X).
7) Вероятность того, что из двух, телевизионных камер в данный момент включена одна, равна 0,42. В студии имеются 20 телевизионных камер. Найти вероятность того, что в данный момент включены:
- 18 камер;
- хотя бы 15 камер. (вероятность включения каждой из камер больше 0,5) .
8) Один из видов продукции производится на трёх фабриках, входящих в состав производственного объединения. Первая фабрика производит 40% всего выпуска продукции, вторая – 35%, третья – 25%. В продукции первой фабрики обнаружено 30% изделий низкого качества, в продукции второй фабрики - 20%, в продукции третьей фабрики 12%. Какова вероятность того, что среди 500 изделий производственного объединения число изделий высшего качества будет 400 до 410.
9) По данным длительной проверки качества запчастей определенного вида брак составляет 5 %. Изготовлено 500 запчастей. Определить математическое ожидание и дисперсию числа годных запчастей.
10) Всхожесть семян некоторого сорта пшеницы составляет 93%. Определить математическое ожидание и дисперсию числа всходов, если высажено 70 семян.
Рекомендуемая литература
1. Вентцель Е.С. Теория вероятностей. Учебник. Издание восьмое, стереотипное. – М.: Высшая школа, 2002 г. - 575 с.
2. Вентцель Е.С., Овчаров Л.А.. Теория вероятностей и её инженерные приложения. Учебное пособие. Издание третье, переработанное и дополненное. – М.: «Академия», 2003 г. – 464 с.
3. Гмурман В.Е. Теория вероятностей и математическая статистика. Учебное пособие. Издание десятое, стереотипное. - М.: Высшая школа», 2004 г. – 480 с.
Тема № 10 Непрерывные случайные величины: функция распределения случайной величины
Вопросы для самостоятельного изучения
1. Функция распределения непрерывной случайной величины
Пример 1. Случайная величина Х задана интегральной функцией
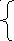0,
при
F(x)
=
1, при х>1
Определить:
а) дифференциальную функцию f(х),
б) вероятность
в) числовые
характеристики: М(Х), D(Х),
.
Решение.
а) Найдём f(x).
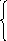0,
при
f(x)
=
=
0, при х>1
б) Вычислим
или
в) Определим
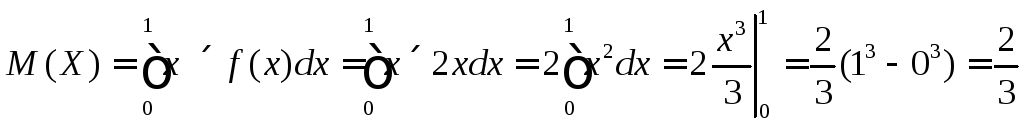
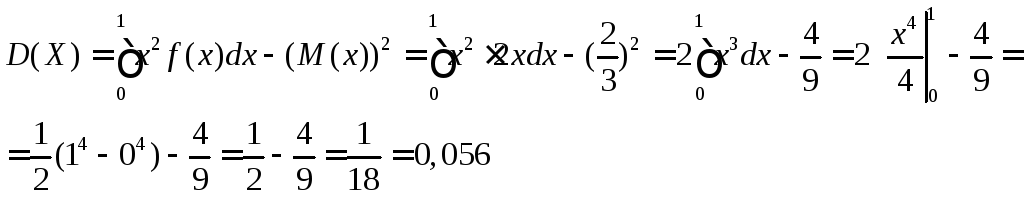
П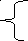
ример
2. Случайная
величина Х задана интегральной функцией:
0,
при
F(x)=
1, при х>e
Определить:
а) дифференциальную функцию f(х)
б) математическое ожидание и дисперсию этой случайной величины.
Решение.
а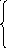
)
0, при
F(x)=
1, при х>e
б)
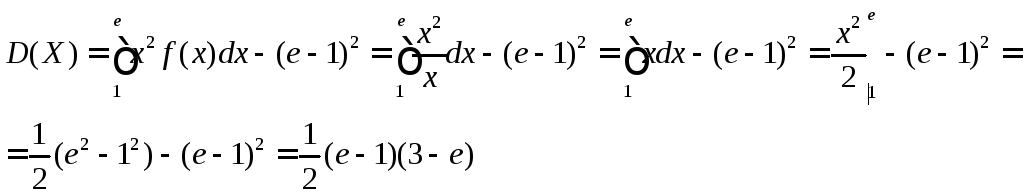
Задания для самостоятельной работы
1) Случайная величина Х задана интегральной функцией:
0
при
F(x)=
1 при х >3
определить:
а)дифференциальную функцию f(х);
б) вероятность того, что Х примет значение, принадлежащее интервалу (2,5;3,5)
2) Случайная величина Х задана интегральной функцией:
0
при
F(x)=
1 при х>3
определить:
а) вероятность того, что Х примет значение, принадлежащее интервалу (1/2;1);
б) математическое ожидание и дисперсию этой случайной величины.
Случайная величина Х задана дифференциальной функцией:
0
при
f(x)=
.
0
при х>
/3
Определить
вероятность того, Х примет значение,
принадлежащее интервалу
.
4) Случайная величина Х задана дифференциальной функцией:
0
при
f(x)=
0 при х>2
Определить:
а) коэффициент а;
б) математическое ожидание и дисперсию этой случайной величины.
5) Случайная величина задана дифференциальной функцией:
0
при
f(x)=
0
при
Определить:
а) коэффициент а;
б) интегральную функцию;
в) математическое ожидание и дисперсию этой случайной величины.
6) Случайная величина Х задана дифференциальной функцией:
0
при
f(x)=
0
при
Определить:
а) интегральную функцию;
б) математическое ожидание и дисперсию этой случайной величины.
7) Случайная величина Х задана дифференциальной функцией:
0
при
f(x)=
0
при
Определить:
а) коэффициент а;
б) вероятность
того, что случайная величина Х примет
значение, принадлежащее интервалу
(0;
);
в) математическое ожидание и дисперсию этой величины.
8) Случайная величина Х задана интегральной функцией:
0
при
F(x)=
1 при х>3
Определить:
а) Вероятность того, Х примет значение, принадлежащее интервалу (1/2;1);
б) математическое ожидание и дисперсию этой случайной величины.
9) Случайная величина Х задана интегральной функцией:
0
при
F(x)
=
1 при х>1
Определить:
а) вероятность того, что Х примет значение, принадлежащее интервалу (1/2;3/2);
б) математическое ожидание и дисперсию этой случайной величины.
Рекомендуемая литература
1. Вентцель Е.С. Теория вероятностей. Учебник. Издание восьмое, стереотипное. – М.: Высшая школа, 2002 г. - 575 с.
2. Вентцель Е.С., Овчаров Л.А.. Теория вероятностей и её инженерные приложения. Учебное пособие. Издание третье, переработанное и дополненное. – М.: «Академия», 2003 г. – 464 с.
3. Гмурман В.Е. Теория вероятностей и математическая статистика. Учебное пособие. Издание десятое, стереотипное. - М.: Высшая школа», 2004 г. – 480 с.
Тема № 11 Плотность вероятности. Числовые характеристики. Моменты случайных величин
Вопросы для самостоятельного изучения
1. Плотность распределения непрерывной случайной величины для определения вероятности попадания случайной величины на интервал.
2. Числовые характеристики непрерывных случайных величин.
Контрольные вопросы
1. Дать определение плотности распределения вероятностей непрерывной случайной величины Х.
2. Дать определение непрерывной случайная величина.
3. Дать определение математическому ожиданию непрерывной случайной величины Х.
4. Дать определение дисперсии непрерывной случайной величины.
5. Дать определение среднеквадратичного отклонения.
6. Дать определение моды М0 дискретной случайной величины.
7. Дать определение медианы MD случайной величины Х.
8. Дать определение начального момента порядка k случайной величины Х.
9. Дать определение центрального момента порядка k случайной величины Х.
10. Дать определение коэффициента асимметрии.
11. Для чего используется величина, называемая эксцессом?
12. Дать определение среднего арифметического отклонения.
Рекомендуемая литература
1. Вентцель Е.С. Теория вероятностей. Учебник. Издание восьмое, стереотипное. – М.: Высшая школа, 2002 г. - 575 с.
2. Вентцель Е.С., Овчаров Л.А.. Теория вероятностей и её инженерные приложения. Учебное пособие. Издание третье, переработанное и дополненное. – М.: «Академия», 2003 г. – 464 с.
3. Гмурман В.Е. Теория вероятностей и математическая статистика. Учебное пособие. Издание десятое, стереотипное. - М.: Высшая школа», 2004 г. – 480 с.
Тема № 12 Законы распределения непрерывных величин: нормальное, равномерное, показательное
Вопросы для самостоятельного изучения
1. Нормальное распределение.
Пример 1. Вес вылавливаемых в пруду рыб подчиняется нормальному закону с математическим ожиданием, равным 375 г, и среднеквадратическим отклонением 25 г. Определить вероятность того, что вес одной пойманной рыбы будет заключен в пределах от 300 до 400г.
Решение.
Дано: М(Х)=а=375 г.,
г.,
с=300г.,d=400г.
Найдем искомую вероятность.
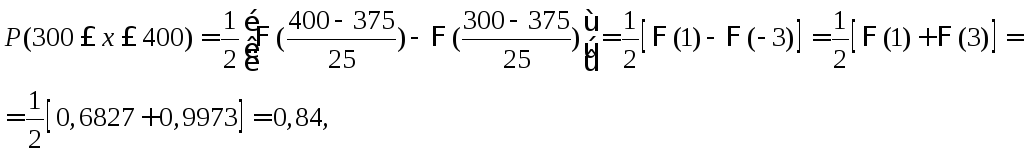
где функции Лапласа Ф(1) = 0,6827, Ф(3) = 0,9973.
Пример 2. Ошибка измерения прибора подчиняется нормальному распределению. С вероятностью 0,92 ошибка измерения не превосходит 4. Найти среднеквадратическое отклонение ошибки прибора. Систематическая ошибка отсутствует.
Решение.
Дано:
,
Воспользовавшись
второй теоремой о нормальной случайной
величине, найдем величину
.
Из таблицы Лапласа,
зная
, найдемt=1,75.
Тогда
или
Ответ:
.
2. Равномерное распределение
Пример 3. Цена деления шкалы прибора 0,5 вольт. При измерениях показания округляются до ближайшего целого деления. Найти вероятность того, что при считывании показаний будет сделана ошибка, не превышающая 0,01 вольт.
Решение.
Дано: Случайная
величина Х -- истинное показание прибора
имен равномерное распределение с
параметрами а=0
, в=0,5.
Тогда
.
Искомая вероятность – это вероятность
показания х либо на
,
либо на
.
Задания для самостоятельной работы
1) Размер детали подчиняется нормальному закону распределения со средней арифметической 15 мм и дисперсией 0,25. Определить ожидаемый процент брака, если допустимые размеры находятся в пределах от 14 мм до 17 мм. Найти выражение интегральной и дифференциальной функции.
2) Изготовленные цехом детали по размерам диаметра распределяются по нормальному закону с математическим ожиданием, равным 4,5 см, и среднеквадратическим отклонением 0,5 см. Определить вероятность того, что размер диаметра наудачу взятой детали отклонится от математического ожидания не более, чем на 1 см.
3) Математическое ожидание нормально распределенной случайной величины равно 15, среднеквадратическое отклонение равно 5. Определить вероятность того, что абсолютная величина отклонения Х-М(Х) будет меньше 10.
4) Ошибка измерения – нормально распределенная случайная величина с дисперсией, равной 100. Систематическая ошибка отсутствует. Найти вероятность того, что ошибка измерения окажется в интервале (3;6).
5) Ошибка взвешивания – случайная нормально распределенная величина с дисперсией 400. Весы заранее настроены на обвес 50 г. Найти вероятность того, что ошибка взвешивания находится в пределах от 30 до 70 г.
6) Автобус некоторого маршрута идет с интервалом в десять минут. Пассажир в какой-то момент подходит к остановке. Время, в течении которого пассажир ожидает автобус, представляет случайную величину, имеющую равномерное распределение. Определить дифференциальную функцию распределения этой случайной величины, ее математическое ожидание и дисперсию.
7) По данным задачи 6 определить вероятность того, что пассажир подошедший к остановке, будет ждать автобус менее 4 минут.
8) Цена деления шкалы измерительного прибора равна 0,2. Показания прибора округляют до ближайшего целого деления. Найти вероятность того, что при отсчёте будет сделана ошибка:
а) меньшая 0,04;
б) большая 0,05.
9) Минутная стрелка электрических часов перемещается скачком в конце каждой минуты. Найти вероятность того, что в данное мгновение часы покажут время, которое отличается от истинного не более чем на 20 сек.
Рекомендуемая литература
1. Вентцель Е.С. Теория вероятностей. Учебник. Издание восьмое, стереотипное. – М.: Высшая школа, 2002 г. - 575 с.
2. Вентцель Е.С., Овчаров Л.А.. Теория вероятностей и её инженерные приложения. Учебное пособие. Издание третье, переработанное и дополненное. – М.: «Академия», 2003 г. – 464 с.
3. Гмурман В.Е. Теория вероятностей и математическая статистика. Учебное пособие. Издание десятое, стереотипное. - М.: Высшая школа», 2004 г. – 480 с.
Тема № 13 Понятие закона больших чисел
Вопросы для самостоятельного изучения
1. Закон больших чисел.
Контрольные вопросы
1. Дать определение характеристической функции случайной величины Х.
2. Дать определение теоремы неравенства Чебышева.
3. Дать определение теоремы Чебышева.
4. Дать определение теоремы Бернулли.
5. Дать определение теоремы Пуассона.
6. Дать определение теоремы Муавра – Лапласа.
Рекомендуемая литература
1. Гмурман В.Е. Теория вероятностей и математическая статистика. Учебное пособие. Издание десятое, стереотипное. - М.: Высшая школа», 2004 г. – 480 с.