
080100Экономика(МатАнализ и ЛинАлгебра) / Линейная алгебра_080100_заоч_1_курс_экз_паспорт
.pdf
S: Установите соответствие между уравнением прямой и её угловым коэффициентом
L1:  L2:
L2: 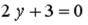
L3: 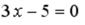
R1:
R2: 0
R3: не существует
R4:
R5: 3
I:
S: Установите соответствие между уравнением прямой и её угловым коэффициентом
L1: 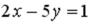 L2:
L2: 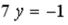 L3:
L3:
R1: 2 5
R2: 0
R3: не существует
R4: − 2 5
R5: -7
I:
S: Установите соответствие между уравнением прямой и её угловым коэффициентом
L1: 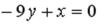 L2:
L2: 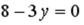 L3:
L3: 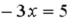
R1:
R3: не существует
R2: 0
R4:
R5: -3
I:
61
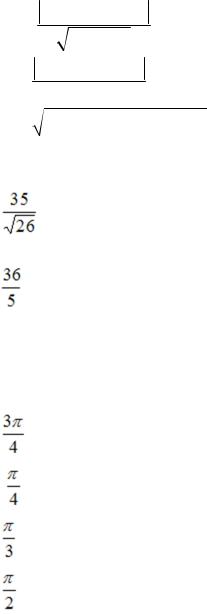
S: Расстояние от точки M (x0 , y0 ) до прямой Ax + By + C = 0 можно найти по формуле
+: d = Ах0 + Ву0 + С

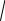 А2 + В2
А2 + В2
-: d = Ах0 + Ву0 + С А2 + В2
-: d = 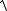
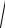 (х2 − х1)2 + ( у2 − у1)2
(х2 − х1)2 + ( у2 − у1)2
I:
S: Расстояние от точки 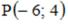 до прямой
до прямой 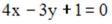 равно …
равно …
-: +: 7
-:
-: 35
I:
S: Острый угол между прямыми
линиями 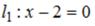 и
и 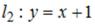 равен …
равен …
-:
+:
-:
-: I:
S: Точка 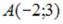 служит основанием перпендикуляра, опущенного из начала координат на прямую линию. Тогда уравнение этой прямой имеет вид …
служит основанием перпендикуляра, опущенного из начала координат на прямую линию. Тогда уравнение этой прямой имеет вид …
-: 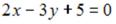 +:
+: 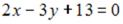 -:
-: 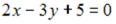
-: 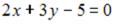 I:
I:
62

S: Каноническое уравнение прямой линии, проходящей через точку
…
,  ,
,
расположения
значениями
R1: 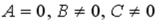
R2: 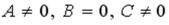
R3: 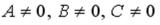
R4: 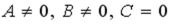
R5: 
I:
S: Выберите уравнение прямой, соответствующее данному рисунку.
-:
63
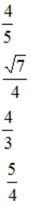
-: 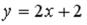 +:
+: 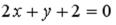
-: 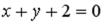
I:
S: Прямые 2x + 3y + 3 = 0 и 4x + ky − 2 = 0 параллельны при k = ...
+: 6
I:
S: Прямые kx − 2 y + 5 = 0 и 3x − y − 3 = 0 параллельны при k = ...
+: 6
I:
S: Прямые 4x + 2 y + 7 = 0 и kx − y − 2 = 0 параллельны при k = ...
+: -2
I:
S: Прямые 2x + 4 y + 3 = 0 и x + ky − 2 = 0 перпендикулярны при k = ...
+: -1/2
I:
S: Прямые kx − y + 3 = 0 и 2x − 4 y − 2 = 0 перпендикулярны при k = ...
+: -2
V2: Кривые второго порядка.
I:
S: Эксцентриситет гиперболы 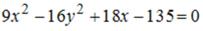 равен …
равен …
-:
-:
-:
+:
I:
S: Расстояние между фокусами эллипса 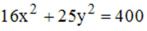 равно …
равно …
+: 6 I:
S: Расстояние между фокусами эллипса 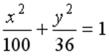 равно …
равно …
+: 16 I:
64

S: Расстояние между фокусами гиперболы |
равно … |
+: 26 |
|
I: |
|
S: Расстояние между фокусами гиперболы |
равно … |
+: 40 |
|
I: |
|
S: Расстояние между фокусами гиперболы |
равно … |
+: 50 |
|
I: |
|
S: Вещественная полуось гиперболы, заданной уравнением 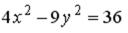 , равна…
, равна…
+: 3 I:
S: Мнимая полуось гиперболы, заданной уравнением 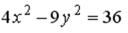 , равна…
, равна…
+: 2 I:
S: Мнимая полуось гиперболы, заданной уравнением 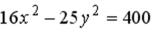 , равна…
, равна…
+: 4 I:
S: Мнимая полуось гиперболы, заданной уравнением 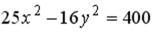 , равна…
, равна…
+:5
I:
S: Большая полуось эллипса, заданного уравнением 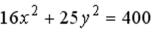 , равна…
, равна…
+: 5 I:
S: Если прямая y = kx уравнение асимптоты гиперболы х2 − у2 = 1, то
4 16
значение k = … +: 2
I:
65

S: Если прямая y = kx уравнение асимптоты гиперболы х2 − у2 = 1, то
1 9
значение k = … +: 3
I:
S: Если прямая y = kx уравнение асимптоты гиперболы х2 − у2 = 1, то
9 36
значение k = … +: 2
I:
S: Уравнение 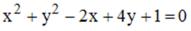 определяет окружность с центром в точке …
определяет окружность с центром в точке …
+: 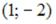 -:
-: 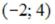 -:
-: 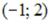
-: 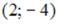 I:
I:
S: Соотношение 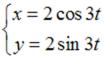 на плоскости
на плоскости 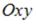 задает … -: гиперболу -: эллипс -: параболу
задает … -: гиперболу -: эллипс -: параболу
+: окружность
I:
S: С помощью преобразования параллельного переноса осей координат
уравнение кривой 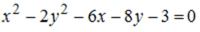 приводится к каноническому виду…
приводится к каноническому виду…
+:
-:
-:
-:  I:
I:
66

S: Укажите соответствие между уравнениями и видами кривых второго порядка.
L1: 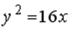
L2:
L3:
R1: Парабола
R2: Эллипс
R3: Гипербола
R4: окружность
I:
S: Укажите соответствие между уравнениями и видами кривых второго порядка.
L1:
L2: 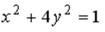
L3: 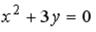
R1: окружность R2: эллипс R3: парабола R4: гипербола
I:
S: Укажите соответствие между уравнениями и видами кривых второго порядка.
L1:  L2:
L2: 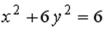
L3:
R1: парабола
R2: эллипс R3: окружность R4: гипербола
I:
S: Укажите соответствие между уравнениями и видами кривых второго порядка.
L1:
67

L2:
L3:
R1: парабола
R2: гипербола
R3: эллипс R4: окружность
I:
S: Укажите соответствие между уравнениями и видами кривых второго порядка.
L1:
L2: 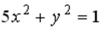
L3: 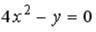
R1: окружность R2: эллипс R3: парабола R4: гипербола
I:
S: Укажите соответствие между уравнениями и видами кривых второго порядка.
L1: 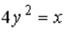 L2:
L2: 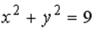
L3:
R1: парабола
R2: окружность
R3: гипербола
R4: эллипс
I:
S: Укажите соответствие между уравнениями и видами кривых второго порядка.
L1:  L2:
L2: 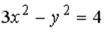
L3:
68

R1: парабола
R2: гипербола
R3: эллипс R4: окружность
I:
S: Укажите соответствие между уравнениями и видами кривых второго порядка.
L1: 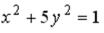 L2:
L2: 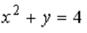
L3:
R1: эллипс
R2: парабола
R3: гипербола
R4: окружность
I:
S: Укажите соответствие между уравнениями и видами кривых второго порядка.
L1: 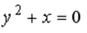
L2:
L3:
R1: парабола
R2: окружность
R3: гипербола
R4: эллипс
I:
S: Укажите соответствие между уравнениями и видами кривых второго порядка.
L1: 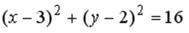 L2:
L2: 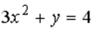
L3: 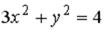
R1: окружность
R2: парабола
R3: эллипс
R4: гипербола
69

V1: Аналитическая геометрия в пространстве
V2: Прямоугольные координаты в пространстве.
I:
равноудалена от точки M имеет координаты …
лежат на одной прямой. Точка точка B имеет координаты …
симметрично относительно равно 6. Тогда точка A может
V2: Плоскость и прямая в пространстве.
I:
S: Общее уравнение плоскости, проходящей через точку 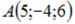 и отсекающей равные отрезки на координатных осях, имеет вид …
и отсекающей равные отрезки на координатных осях, имеет вид …
-:
+: 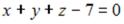 -:
-: 
-: 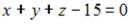 I:
I:
S: Нормальный вектор плоскости 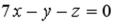 имеет координаты…
имеет координаты…
-: (7; 0; – 1)
70
