
Matematika_260800_080200_100100_och_poln_ekz
.pdf
S: Бросают игральную кость. Вероятность того, что выпадет любое число очков, кроме 5, равна …
1
-: Р
3
+: Р 5
6
-: Р 1
4
V2: Теоремы сложения и умножения вероятностей. Полная вероятность. Формула Байеса
I:
S: В урне лежат 12 шаров, среди которых 10 шаров белые. Наудачу по одному извлекают три шара без возвращения. Тогда вероятность того, что все три шара будут белыми, равна …
-: 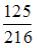 -:
-: 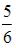 -:
-: 
+: 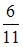 I:
I:
S: В урне лежат 12 шаров, среди которых 7 шаров белые. Наудачу по одному извлекают два шара без возвращения. Тогда вероятность того, что оба шара будут белыми, равна …
+: 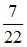 -:
-: 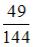 -:
-: 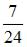
-: 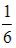 I:
I:
S: В урне находится 5 белых и 2 чѐрных шара. Из урны по очереди вынимаются четыре шара. Вероятность того, что все шары будут белыми, равна …
4
-: Р
7
-: Р 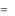 5
5
7
51

-:
+:
1
Р
2
1
Р
7
I:
S: В урне находится 5 белых и 3 чѐрных шара. Из урны по очереди вынимаются четыре шара. Вероятность того, что все шары будут белыми, равна …
3
-: Р
5
-: Р 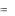 4
4
5
-: Р 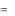 3
3
4
+: Р 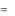 1
1
14
I:
S: В урне находятся 3 белых и 3 чѐрных шара. Из урны по очереди вынимаются два шара. Вероятность того, что все шары будут белыми, равна
…
-: 1/4 +: 1/5 -: 9/10 -: 2/15 I:
S: В ящике 4 лампочки, одна из которых бракованная. Наугад по очереди вынимают три. Вероятность того, что все вынутые лампочки будут исправны, равна …
-: Р=0,33
+: Р=0,25 -: Р=0,5
I:
S: Устройство состоит из двух элементов, работающих независимо. Вероятности безотказной работы этих элементов (в течение рабочего дня) равны соответственно 0,8 и 0,9. Тогда вероятность того, что в течение рабочего дня будут работать безотказно оба элемента, равна …
-: 0,08 +: 0,72 -: 0,85 -: 0,18 I:
52
S: Прибор состоит из двух элементов, работающих независимо. Вероятность выхода из строя первого элемента равна 0,2; вероятность выхода из строя второго элемента равна 0,3. Вероятность того, что оба элемента выйдут из строя, равна …
-: 0,3 -: 0,2 +: 0,06 -: 0,56 I:
S: Прибор состоит из двух элементов, работающих независимо. Вероятность выхода из строя первого элемента равна 0,2; вероятность выхода из строя второго элемента равна 0,3. Вероятность того, что оба элемента будут работать, равна …
-: 0,3 -: 0,2 +: 0,56 -: 0,06 I:
S: Прибор состоит из двух элементов, работающих независимо. Вероятности безотказной работы первого элемента равна 0,75; вероятность безотказной работы второго элемента равна 0,9. Вероятность того, что оба элемента выйдут из строя, равна … Вероятность того, что оба элемента выйдут из строя, равна …
-: 0,075 +: 0,025 -: 0,35 -: 0,225 I:
S: Прибор состоит из двух элементов, работающих независимо. Вероятности безотказной работы первого элемента равна 0,75; вероятность безотказной работы второго элемента равна 0,9. Вероятность того, что оба элемента будут работать, равна …
-: 0,075 -: 0,025 -: 0,35 +: 0,675 I:
S: Два стрелка производят по одному выстрелу. Вероятности попадания в цель для первого и второго стрелков равны 0,5 и 0,4 соответственно. Тогда вероятность того, что в цель попадут оба стрелка, равна…
-: Р=0,16 -: Р=0,9 -: Р=0,3 +: Р= 0,2 I:
53
S: Два стрелка производят по одному выстрелу. Вероятности попадания в цель для первого и второго стрелков равны 0,5 и 0,3 соответственно. Тогда вероятность того, что в цель попадут оба стрелка, равна…
+: Р=0,15 -: Р=0,8 -: Р=0,12 -: Р=0,35 I:
S: Два стрелка производят по одному выстрелу. Вероятности попадания в цель для первого и второго стрелков равны 0,7 и 0,4 соответственно. Тогда вероятность того, что в цель попадут оба стрелка, равна…
-: Р=0,4 -: Р=0,35 -: Р=0,3 +: Р=0,28 I:
S: Два стрелка производят по одному выстрелу. Вероятности попадания в цель для первого и второго стрелков равны 0,8 и 0,3 соответственно. Тогда вероятность того, что в цель попадут оба стрелка, равна…
-: Р=0,3 -: Р=0,32 +: Р=0,24 -: Р=0,5 I:
S: По оценкам экспертов вероятности банкротства для двух предприятий, производящих разнотипную продукцию, равны 0,1 и 0,05. Тогда вероятность банкротства обоих предприятий равна…
+: Р=0,005 -: Р=0,855 -: Р=0,05 -: Р=0,15 I:
S: В первой урне 8 черных и 2 белых шаров. Во второй урне 3 белых и 7 черных шаров. Из наудачу взятой урны вынули один шар. Тогда вероятность того, что этот шар окажется белым, равна …
-: 0,55 -: 0,75 +: 0,25 -: 0,5 I:
S: В первой урне 5 белых и 5 черных шаров. Во второй урне 3 черных и 7 белых шаров. Из наудачу взятой урны вынули один шар. Тогда вероятность того, что этот шар окажется белым, равна…
-: 0,1 -: 0,65
54
+: 0,6 -: 0,12 I:
S: В первой урне 3 белых и 7 черных шаров. Во второй урне 4 белых и 6 черных шаров. Из наудачу взятой урны вынули один шар. Тогда вероятность того, что этот шар окажется белым, равна…
-: 0,7 -: 0,4 +: 0,35 -: 0,7 I:
S: Имеются две одинаковые на вид урны. В первой урне находятся один белый и два чѐрных шара. Во второй урне – два белых и два чѐрных шара. Из наудачу взятой урны взяли один шар. Тогда вероятность того, что этот шар окажется белым равна …
-: 5/6 +: 5/12 -: 1/2 -: 3/7 I:
S: Имеются две одинаковые на вид урны. В первой урне находятся три красных и один чѐрный шар. Во второй – два красных и один чѐрный шар. Из наудачу взятой урны взяли один шар. Тогда вероятность того, что этот шар красный равна …
-: 5/14 +: 17/24 -: 17/12 -: 2/3
I:
S: Имеются две одинаковые на вид урны. В первой урне находятся два белых
иодин чѐрный шар. Во второй урне – семь белых и семь чѐрных шаров. Из наудачу взятой урны взяли один шар. Тогда вероятность того, что этот шар белый равна …
-: 9/17 -: 2/5 -: 3/5 +: 7/12 I:
S: Имеются две одинаковые на вид урны. В первой урне находятся два белых
иодин чѐрный шар. Во второй урне – семь белых и семь чѐрных шаров. Из наудачу взятой урны взяли один шар, который оказался черным. Тогда вероятность того, что этот шар из первой урны, равна …
-: 9/17 +: 2/5 -: 3/5
55

-: 5/12 I:
S: Имеются две одинаковые на вид урны. В первой урне находятся два белых и один чѐрный шар. Во второй урне – семь белых и семь чѐрных шаров. Из наудачу взятой урны взяли один шар, который оказался черным. Тогда вероятность того, что этот шар из второй урны, равна …
-: 9/17 +: 3/5 -: 2/5 -: 5/12 I:
S: С первого станка на сборку поступает 40% изготовленных деталей, со второго – 30%, а с третьего – 30%. Вероятность изготовления бракованной детали для каждого станка равна соответственно 0,01; 0,03; 0,05. Вероятность того, что наудачу выбранная деталь окажется бракованной, равна …
+: Р ( А ) 0 , 0 2 8
-: -:
Р ( А ) 0 , 0 3 .
Р ( A ) 0 , 0 1 8
I:
S: В ящике содержатся 20 деталей, изготовленных на заводе № 1; 30 деталей, изготовленных на заводе № 2; и 50 деталей, изготовленных на заводе № 3. Вероятность того, что деталь, изготовленная на заводе № 1, отличного качества, равна 0,8; на заводе № 2 – равна 0,7, а на заводе № 3 – равна 0,9. Тогда вероятность того, что наудачу извлеченная деталь окажется отличного качества, равна …
-: 0,80 -: 0,81 +: 0,82 -: 0,92 I:
S: Имеются 3 партии ламп по 20, 30, 50 штук в каждой. Вероятность того, что лампы проработают заданное время, равна для каждой партии, соответственно, 0,7; 0,8 и 0,9. Вероятность того, что выбранная наудачу лампа из 100 данных ламп проработает заданное время, равна …
-: 0,82 -: 0,81 -: 0,80 +: 0,83 I:
56

S: С первого станка на сборку поступает 30%, со второго – 70% всех деталей. Среди деталей первого станка 80% стандартных, второго – 90%. Наудачу взятая деталь оказалась стандартной. Тогда вероятность того, что она поступила на сборку с первого станка, равна …
-: 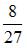
+: 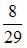 -: 0,87
-: 0,87
-: 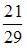 I:
I:
S: С первого станка на сборку поступает 20%, со второго – 80% всех деталей. Среди деталей первого станка 85% стандартных, второго – 95%. Наудачу взятая деталь оказалась нестандартной. Тогда вероятность того, что она поступила на сборку со второго станка, равна …
+: 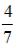 -:
-: 
-: 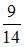 -: 0,07
-: 0,07
V2: Законы распределения вероятностей случайных величин
I:
S: Дискретная случайная величина 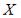 задана законом распределения вероятностей:
задана законом распределения вероятностей:
Тогда значение a равно …
-: 0,5 -: 0,6 +: 0,4 -: – 0,6 I:
S: Дискретная случайная величина 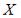 задана законом распределения вероятностей:
задана законом распределения вероятностей:
Тогда ее функция распределения вероятностей имеет вид …
57

-:
+:
-:
-: I:
S: Дискретная случайная величина 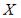 задана законом распределения вероятностей:
задана законом распределения вероятностей:
Тогда ее функция распределения вероятностей имеет вид …
-:
-:
-:
+:
58
I:
S: Дискретная случайная величина 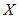 задана законом распределения вероятностей:
задана законом распределения вероятностей:
Тогда значения a и b могут быть равны …
-: 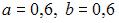 -:
-: 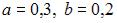 +:
+: 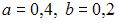
-:  I:
I:
S: Дан закон распределения вероятностей дискретной случайной величины Х:
Тогда значение a равно…
-: 0,3 -: 0,7 -: 0,2 +: 0,1 I:
S: Дан закон распределения вероятностей дискретной случайной величины Х:
Тогда значение a равно…
-: 0,2 -: 0,3 +: 0,4 -: 0,6 I:
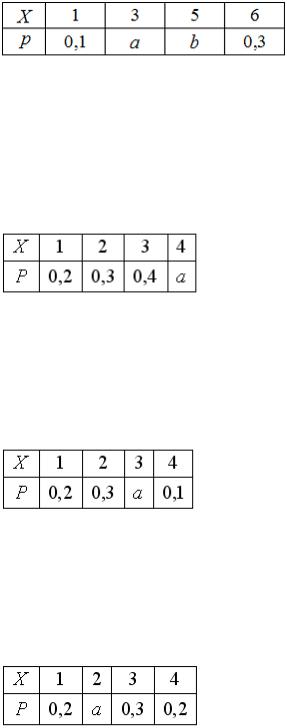
S: Дан закон распределения вероятностей дискретной случайной величины Х:
Тогда значение a равно…
-: 0,2 +: 0,3 -: 0,5 -: 0,7 I:
59
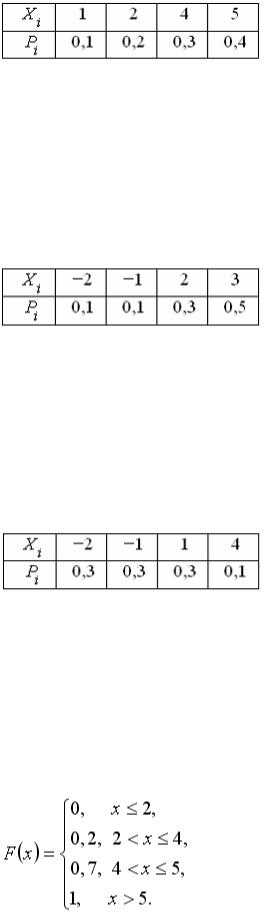
S: Дискретная случайная величина Х задана законом распределения вероятностей
Тогда значение интегральной функции распределения вероятностей 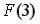 равно …
равно …
+: 0,3 -: 0,9 -: 0,2 -: 0,7 I:
S: Дискретная случайная величина Х задана законом распределения вероятностей
Тогда значение интегральной функции распределения вероятностей 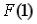 равно …
равно …
+: 0,2 -: 0,8 -: 0,6 -: 0,9 I:
S: Дискретная случайная величина Х задана законом распределения вероятностей
Тогда значение интегральной функции распределения вероятностей 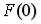 равно …
равно …
-: 0,4 +: 0,6 -: 0,3 -: 0,9 I:
S: Функция распределения вероятностей дискретной случайной величины 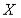 имеет вид
имеет вид
60
