
Matematika_260800_080200_100100_och_poln_ekz
.pdfS: Функция 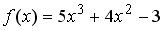 разложена в ряд Тейлора по степеням (х–1).
разложена в ряд Тейлора по степеням (х–1).
Тогда коэффициент при 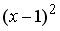 равен …
равен …
-: 23 +: 19 -: 4 -: 38 I:
S: Функция 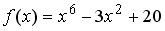 разложена в ряд Тейлора по степеням (х–1).
разложена в ряд Тейлора по степеням (х–1).
Тогда коэффициент при 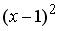 равен …
равен …
-: 0 -: - 1 -: 24 +: 12 I:
S: Если 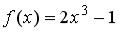 , то коэффициент
, то коэффициент 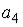 разложения данной функции в ряд Тейлора по степеням (х–1) равен…
разложения данной функции в ряд Тейлора по степеням (х–1) равен…
-: 1 -: 0,25 +: 0 -: 2
I:
S: Если 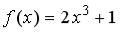 , то коэффициент
, то коэффициент 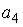 разложения данной функции в ряд Тейлора по степеням (х–1) равен…
разложения данной функции в ряд Тейлора по степеням (х–1) равен…
-: 0,5 -: 1 -: 2 +: 0 I:
S: Если 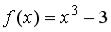 , то коэффициент
, то коэффициент 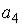 разложения данной функции в ряд по степеням (х+3) равен...
разложения данной функции в ряд по степеням (х+3) равен...
+: 0 -: 1 -: 3
-: 0,25 I:
S: Если 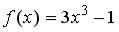 , то коэффициент
, то коэффициент 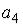 разложения данной функции в ряд по степеням (х+1) равен...
разложения данной функции в ряд по степеням (х+1) равен...
-: 0,75 -: 9
21
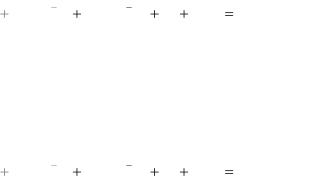
+: 0 -: 3 I:
S: Если 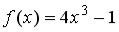 , то коэффициент
, то коэффициент 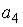 разложения данной функции в ряд по степеням (х-1) равен...
разложения данной функции в ряд по степеням (х-1) равен...
-: 4 -: 12 -: 1 +: 0
V1: Дифференциальные уравнения
V2: Тип дифференциального уравнения
I:
S: Уравнение 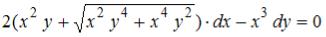 является … -: уравнением Бернулли -: линейным дифференциальным уравнением первого порядка
является … -: уравнением Бернулли -: линейным дифференциальным уравнением первого порядка
-: дифференциальным уравнением с разделяющимися переменными +: однородным относительно 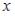 и
и 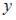 дифференциальным уравнением первого порядка
дифференциальным уравнением первого порядка
I:
S: Дифференциальное уравнение y ( n ) a |
1 |
y ( n 1) |
a |
2 |
y ( n 2 ) |
... a |
n |
y f ( x ) |
|
|
|
|
|
|
называется …
+: линейным неоднородным дифференциальным уравнением n-го порядка; -: линейным однородным дифференциальным уравнением n-го порядка;
-: нелинейным неоднородным дифференциальным уравнением n-го порядка; -: нелинейным однородным дифференциальным уравнением n-го порядка.
I:
S: Дифференциальное уравнение y |
( n ) a y ( n 1) |
a |
2 |
y ( n 2 ) |
... a |
n |
y 0 |
|
1 |
|
|
|
|
называется …
-: линейным неоднородным дифференциальным уравнением n-го порядка; +: линейным однородным дифференциальным уравнением n-го порядка;
-: нелинейным неоднородным дифференциальным уравнением n-го порядка; -: нелинейным однородным дифференциальным уравнением n-го порядка.
I:
S: Дифференциальное уравнение 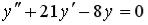 является …
является …
+: линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами -: дифференциальным уравнением Бернулли
-: линейным неоднородным дифференциальным уравнением второго порядка с постоянными коэффициентами -: дифференциальным уравнением с разделяющимися переменными
I:
22
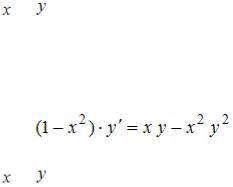
S: Дифференциальное уравнение 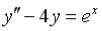 является … -: дифференциальным уравнением Бернулли
является … -: дифференциальным уравнением Бернулли
+: линейным неоднородным дифференциальным уравнением второго порядка с постоянными коэффициентами -: дифференциальным уравнением с разделяющимися переменными
-: линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами
I:
S: Дифференциальное уравнение 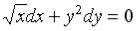 является …
является …
-: линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами +: дифференциальным уравнением первого порядка с разделяющимися переменными
-: линейным неоднородным дифференциальным уравнением второго порядка с постоянными коэффициентами -: дифференциальным уравнением Бернулли
I:
S: Дифференциальное уравнение 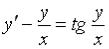 является … -: уравнением Бернулли
является … -: уравнением Бернулли
-: линейным неоднородным дифференциальным уравнением 1 порядка +: однородным дифференциальным уравнением -: уравнением с разделяющимися переменными
I:
S: Дифференциальное уравнение 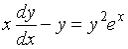 является …
является …
-: дифференциальным уравнением с разделяющимися переменными
-: однородным относительно и |
дифференциальным уравнением первого |
порядка |
|
-: линейным дифференциальным уравнением первого порядка |
|
+: уравнением Бернулли |
|
I: |
|
S: Дифференциальное уравнение |
является … |
-: дифференциальным уравнением с разделяющимися переменными |
|
-: однородным относительно и |
дифференциальным уравнением первого |
порядка |
|
-: линейным дифференциальным уравнением первого порядка +: уравнением Бернулли
I:
S: Дифференциальное уравнение 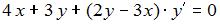 является … -: дифференциальным уравнением с разделяющимися переменными
является … -: дифференциальным уравнением с разделяющимися переменными
23

+: однородным относительно 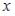 и
и 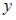 дифференциальным уравнением первого порядка -: уравнением Бернулли
дифференциальным уравнением первого порядка -: уравнением Бернулли
-: линейным дифференциальным уравнением первого порядка
I:
S: Дифференциальное уравнение 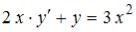 является …
является …
+: линейным неоднородным дифференциальным уравнением первого порядка -: дифференциальным уравнением с разделяющимися переменными
-: уравнением Бернулли -: однородным относительно 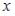 и
и 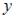 дифференциальным уравнением первого порядка
дифференциальным уравнением первого порядка
I:
S: Дифференциальное уравнение 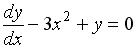 является …
является …
+: линейным неоднородным дифференциальным уравнением первого порядка -: дифференциальным уравнением с разделяющимися переменными
-: уравнением Бернулли -: однородным относительно 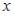 и
и 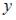 дифференциальным уравнением первого порядка
дифференциальным уравнением первого порядка
I:
S: Из данных уравнений дифференциальным уравнением с разделяющимися переменными является …
-:
-: 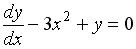 +:
+: 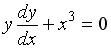
-: 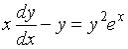 I:
I:
S: Из данных дифференциальных уравнений линейным неоднородным дифференциальным уравнением первого порядка является …
-: +: 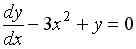
24

-: 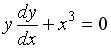
-: 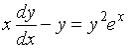 I:
I:
S: Из данных дифференциальных уравнений уравнениями Бернулли являются …
+:
-: 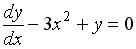 -:
-: 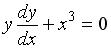
+: 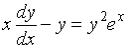 I:
I:
S: Дифференциальное уравнение
F ( x , y , y ', y '', ..., y ( n ) ) 0 называется:
-: уравнением с частными производными; -: обыкновенным дифференциальным уравнением 1-ого порядка;
+: обыкновенным дифференциальным уравнением n-го порядка; -: уравнением с частными производными n-го порядка.
I:
S: Общим решением дифференциального уравнения F ( x , y , y ') 0 называется?
-: |
y |
( x ) |
+: |
y |
( x , C ) |
-: |
y ' |
f ( x , y ) |
-: |
y ' |
f ( x , C ) |
I:
S: Даны два дифференциальных уравнения
1. |
y ' |
f1 ( x ) f 2 ( y ) , |
|
2. |
f1 ( x ) f 2 ( y ) d x |
f 3 ( x ) f 4 ( y ) d y 0 . |
|
Дифференциальными уравнениями с разделяющимися переменными являются … -: Только 1 -: Только 2
-: Ни одно из них +: Оба
I:
25
S: Линейное дифференциальное уравнение первого порядка имеет вид …
-: F ( x , y , y ) 0
-: y f ( x , y )
-: +:
P ( x , y ) d x Q ( x , y ) d y 0 y P ( x ) y Q ( x )
I:
S: Уравнение Бернулли имеет вид …
+: y |
P ( x ) y Q ( x ) y n |
|
-: y P ( x ) Q ( x ) y n |
||
-: |
y |
P ( x ) x Q ( x ) |
-: |
P ( x , y ) d x Q ( x , y ) d y 0 |
|
I:
S: Порядком дифференциального уравнения называется -: наивысшая степень одной из производных уравнения; +: наивысший порядок производных уравнения;
-: сумма всех порядков производных, входящих в уравнение.
I:
S: Среди перечисленных уравнений дифференциальными уравнениями первого порядка являются …
+: 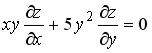
-: +: 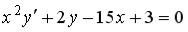
-: I:
S: Среди перечисленных уравнений дифференциальными уравнениями второго порядка являются …
-:
+: -: 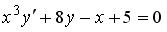
+:
I:
26
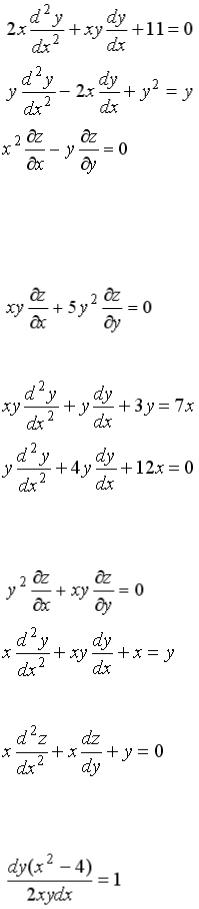
S: Среди перечисленных уравнений дифференциальными уравнениями второго порядка являются …
+:
+:
-:
-: 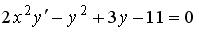 I:
I:
S: Среди перечисленных уравнений дифференциальными уравнениями первого порядка являются …
+:
+: 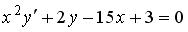
-:
-: I:
S: Среди перечисленных уравнений дифференциальными уравнениями первого порядка являются …
+:
-: +: 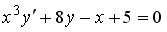
-: I:
S: Среди перечисленных уравнений дифференциальными уравнениями первого порядка являются …
+:
27

+: 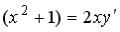 -:
-: 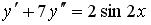
-: I:
S: Среди перечисленных уравнений дифференциальными уравнениями первого порядка являются …
-: 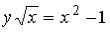
+: 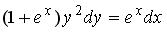 +:
+: 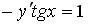
-: 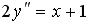 I:
I:
S: Среди перечисленных уравнений дифференциальными уравнениями первого порядка являются …
-: 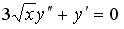 -:
-: 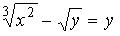
+:
+: 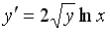 I:
I:
S: Среди перечисленных уравнений дифференциальными уравнениями первого порядка являются …
-: 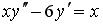 +:
+: 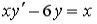 -:
-: 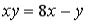
+: 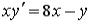 I:
I:
S: Среди перечисленных уравнений дифференциальными уравнениями первого порядка являются …
+: 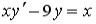 +:
+: 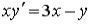 -:
-: 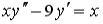
-: 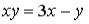
V2: Дифференциальные уравнения первого порядка
I:
28
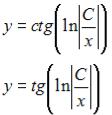
S: Общий интеграл дифференциального уравнения 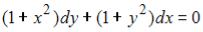 имеет вид …
имеет вид …
-: 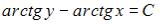 -:
-: 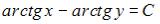 +:
+: 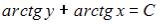
-: 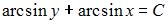 I:
I:
S: Общее решение дифференциального уравнения 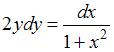 имеет вид
имеет вид
…
-: 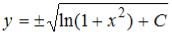 +:
+: 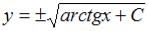 -:
-: 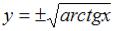
-: 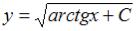 I:
I:
S: Общее решение дифференциального уравнения 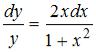 имеет вид …
имеет вид …
-: 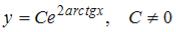 -:
-: 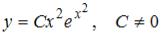 -:
-: 
+: 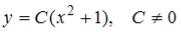 I:
I:
S: Общее решение дифференциального уравнения 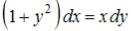 при
при 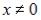 имеет вид …
имеет вид …
-: , 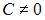
-: , 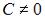 -:
-: 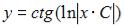 ,
, 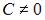
+: 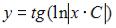 ,
, 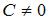 I:
I:
29
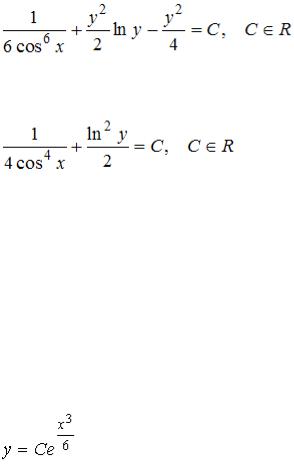
S: Общий интеграл дифференциального уравнения 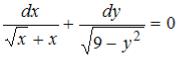 имеет вид…
имеет вид…
-: 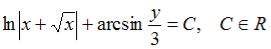 -:
-: 
+: 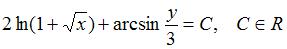
-: 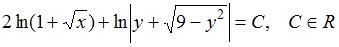 I:
I:
S: Общий интеграл дифференциального уравнения 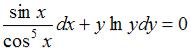 имеет вид…
имеет вид…
-: 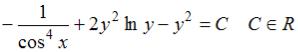
-:
+: 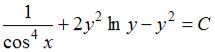 ,
, 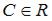
-: I:
S: Общее решение дифференциального уравнения 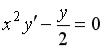 имеет вид
имеет вид
-: 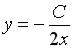 -:
-: 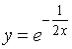 +:
+: 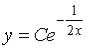
-: I:
30
