
Matematika_260800_080200_100100_och_poln_ekz
.pdf
АВТОНОМНАЯ НЕКОММЕРЧЕСКАЯ ОРГАНИЗАЦИЯ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ ЦЕНТРОСОЮЗА РОССИЙСКОЙ ФЕДЕРАЦИИ «РОССИЙСКИЙ УНИВЕРСИТЕТ КООПЕРАЦИИ»
КАЗАНСКИЙ КООПЕРАТИВНЫЙ ИНСТИТУТ (ФИЛИАЛ)
УТВЕРЖДАЮ Проректор по учебной работе
Казанского кооперативного института (филиала) Российского университета кооперации
/А. М. Хуснутдинова/ «11» сентября 2013 г.
МАТЕМАТИКА
ТЕСТОВЫЕ ЗАДАНИЯ
Тестовые задания обсуждены на заседании кафедры инженернотехнических дисциплин и сервиса «31» августа 2013 г. протокол № 1
Заведующий кафедрой |
/А.М. Мухаметшин/ |
СОГЛАСОВАНО |
|
Начальник отдела менеджмента качества |
/Д.Н. Алюшева/ |
1
ПАСПОРТ
№ |
Наименование пункта |
Значение |
1. |
Кафедра |
Инженерно-технические |
|
|
дисциплины и сервис |
2. |
Автор – разработчик |
Поташев А.В., д.ф.-м.н., профессор |
|
|
Поташева Е.В., к.т.н., доцент |
3. |
Наименование дисциплины |
Математика |
|
|
|
4. |
Общая трудоемкость по |
180 (2 семестр) |
|
учебному плану |
|
5. |
Вид контроля (нужное |
Предварительный (входной), |
|
подчеркнуть) |
текущий, промежуточный |
|
|
(экзамен) |
6. |
Для специальности(ей)/ |
260800.62 «Технология |
|
направления(й) подготовки |
продукции и организация |
|
|
общественного питания», |
|
|
080200.62 «Менеджмент», |
|
|
100100.62 «Сервис», |
|
|
нормативный срок |
|
|
очная форма обучения |
7. |
Количество тестовых заданий |
371 |
|
всего по дисциплине, из них |
|
|
|
|
8. |
Количество заданий при |
30 |
|
тестировании студента |
|
|
|
|
9. |
Из них правильных ответов |
|
|
(в %): |
|
10. |
для оценки «отлично» |
85 % и больше |
|
|
|
11. |
для оценки «хорошо» |
70 % - 85% |
|
|
|
12. |
для оценки |
50% - 70% |
|
«удовлетворительно» |
|
|
или для получения оценки |
- |
|
«зачет» не менее |
|
13. |
Время тестирования (в |
45 |
|
минутах) |
|
2
Содержание |
|
|
Стр. |
V1: РЯДЫ................................................................................................................. |
4 |
V2: Числовые последовательности ................................................................... |
4 |
V2: Признаки сходимости числовых рядов...................................................... |
8 |
V2: Сходимость знакоположительных числовых рядов ............................... |
10 |
V2: Сходимость знакочередующихся числовых рядов................................. |
13 |
V2: Область сходимости степенных рядов .................................................... |
15 |
V2: Разложение функций в степенные ряды .................................................. |
18 |
V1: ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ.................................................... |
22 |
V2: Тип дифференциального уравнения......................................................... |
22 |
V2: Дифференциальные уравнения первого порядка ................................... |
28 |
V2: Линейные дифференциальные уравнения высших порядков ............... |
38 |
V2: Дифференциальные уравнения высших порядков, допускающие |
|
понижение порядка ........................................................................................... |
44 |
V1: ТЕОРИЯ ВЕРОЯТНОСТЕЙ.......................................................................... |
47 |
V2: Определение вероятности ......................................................................... |
47 |
V2: Теоремы сложения и умножения вероятностей. Полная вероятность. |
|
Формула Байеса................................................................................................. |
51 |
V2: Законы распределения вероятностей случайных величин .................... |
57 |
V2: Числовые характеристики случайных величин ...................................... |
68 |
V1: МАТЕМАТИЧЕСКАЯ СТАТИСТИКА....................................................... |
73 |
V2: Статистическое распределение выборки. Характеристики |
|
вариационного ряда .......................................................................................... |
73 |
V2: Точечные и интервальные оценки параметров распределения............. |
81 |
V2: Проверка статистических гипотез............................................................ |
88 |
3

F1: Математика экзамен 2 семестр 2013/2014 F2: Поташев А.В., Поташева Е.В.
F3: Тестовые задания по направлению подготовки 260800.62 «Технология продукции и организация общественного питания» очная нормативный срок 371 задания, 17 вопросов, 180 часов
F4: Дидактическая единица; Раздел; Тема
V1: Ряды
V2: Числовые последовательности
I:
S: Второй член  числовой последовательности
числовой последовательности  равен
равен
+: 16 I:
S: Второй член 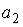 числовой последовательности
числовой последовательности 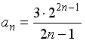 равен
равен
+: 8 I:
S: Второй член 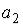 числовой последовательности
числовой последовательности  равен …
равен …
+: 7 I:
S: Четвертый член 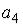 числовой последовательности
числовой последовательности 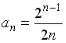 равен …
равен …
+: 1 I:
S: Четвертый член  числовой последовательности
числовой последовательности 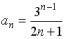 равен …
равен …
+: 3 I:
S: |
-й член числовой последовательности |
равен… |
-:
+:
-: I:
4

S: |
-й член числовой последовательности |
равен… |
-: |
|
|
|
|
|
+: |
|
|
|
|
|
-: |
|
|
|
|
|
-: |
|
|
|
|
|
I: |
|
|
|
|
|
S: Последовательность задана рекуррентным соотношением a n 1 |
4 a n |
9 , |
|||
a1 |
3 . Тогда четвертый член этой последовательности a 4 |
равен… |
|
|
|
-: -5 |
|
|
|
|
|
-: -13 |
|
|
|
|
|
-: -61 |
|
|
|
|
|
+: 3 |
|
|
|
|
|
I: |
|
|
|
|
|
S: Последовательность задана рекуррентным соотношением a n 1 |
a n |
1 6 , |
|||
2 |
|
||||
|
|
|
|
|
|
a1 |
1 6 . |
|
|
|
|
Тогда четвертый член этой последовательности a 4 равен… |
|
|
|
||
-: 31 |
|
|
|
|
|
+: 30 |
|
|
|
|
|
-: 28 |
|
|
|
|
|
-: 32 |
|
|
|
|
|
I: |
|
|
|
|
|
S: Последовательность задана рекуррентным соотношением a n 1 |
4 a n |
3 , |
|||
a1 |
1 . Тогда четвертый член этой последовательности a 4 |
равен… |
|
|
|
-: -5 |
|
|
|
|
|
-: -13 |
|
|
|
|
|
-: -61 |
|
|
|
|
|
+: 1 |
|
|
|
|
|
I: |
|
|
|
|
|
S: Последовательность задана рекуррентным соотношением a n 1 |
2 a n |
3 , |
|||
a1 |
2 . Тогда четвертый член этой последовательности a 4 |
равен… |
|
|
|
+: -5 -: -13 -: -61 -: 1
5

I: |
|
|
|
|
|
|
|
S: Последовательность задана рекуррентным соотношением a |
n 1 |
a |
2 |
3 , a |
1 |
2 |
|
|
|
|
n |
|
|
||
. Тогда четвертый член этой последовательности a 4 равен… |
|
|
|
|
|
|
|
-: -5 |
|
|
|
|
|
|
|
-: -13 |
|
|
|
|
|
|
|
-: -61 |
|
|
|
|
|
|
|
+: 1 |
|
|
|
|
|
|
|
I: |
|
|
|
|
|
|
|
S: Наибольшее значение предела при n |
имеет последовательность … |
|
|
||||
+:
-:
-:
n
1
1
n
1
n
2 n 2
n 2 1
-: |
n 2 |
|
2 n 2 1 |
|
|
|
|
|
I: |
|
|
S: Наибольшее значение предела при n |
имеет последовательность … |
|
-:
-:
n
1
1
n
1
n
+:
-:
2 n 2
n 2 |
1 |
n 2 |
|
2 n 2 |
1 |
I:
S: Бесконечно малой числовой последовательностью является последовательность …
-:
-:
-:
+:
I:
|
|
n 2 |
2 |
|
|
||
|
n 2 |
n |
1 |
|
|||
|
n 2 |
1 |
|
|
|
||
|
|
n |
|
|
|
|
|
2 n |
1 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
n |
|
|
||
|
|
|
|
|
|
||
|
|
n 2 |
|
n |
1 |
||
6
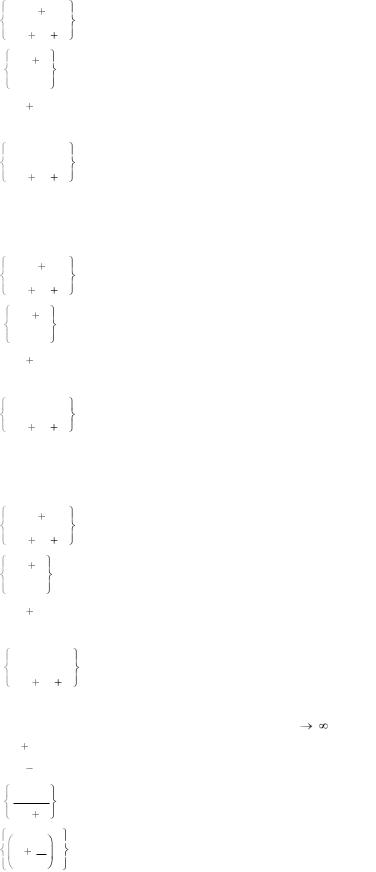
S: Бесконечно малой числовой последовательностью является последовательность …
-:
+:
|
n 2 |
2 |
|
n 2 |
n 1 |
||
|
n 2 |
1 |
|
|
n 3 |
|
|
-: |
2 n |
1 |
|
|
|
n |
|
|
|
|
|
|
|
|
-: |
|
|
n 3 |
|
|
n 2 |
n 1 |
||
|
|
|||
I:
S: Бесконечно большой числовой последовательностью является последовательность …
-:
+:
-:
-:
|
|
n 2 |
|
|
2 |
|
n 2 |
n |
1 |
||
|
|
n 2 |
1 |
|
|
|
|
n |
|
|
|
2 n |
1 |
|
|
||
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
n |
|
|
|
|
|
|
||
|
n 2 |
n |
1 |
||
I:
S: Бесконечно большой числовой последовательностью является последовательность …
-:
-:
-:
+:
|
|
n 2 |
2 |
|
|
||
|
n 2 |
n |
1 |
|
|||
|
n 2 |
1 |
|
|
|
||
|
|
n 3 |
|
|
|
|
|
2 n |
1 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
n 3 |
|
|
||
|
|
n 2 |
|
n |
1 |
||
I: |
|
|
|
|
S: Наименьшее значение предела при n |
имеет последовательность … |
|||
-: |
n |
1 |
|
|
|
|
|
|
|
2 n |
1 |
|
|
|
|
|
|
||
+:
-:
n
n 2 1
n
1
1
n
7
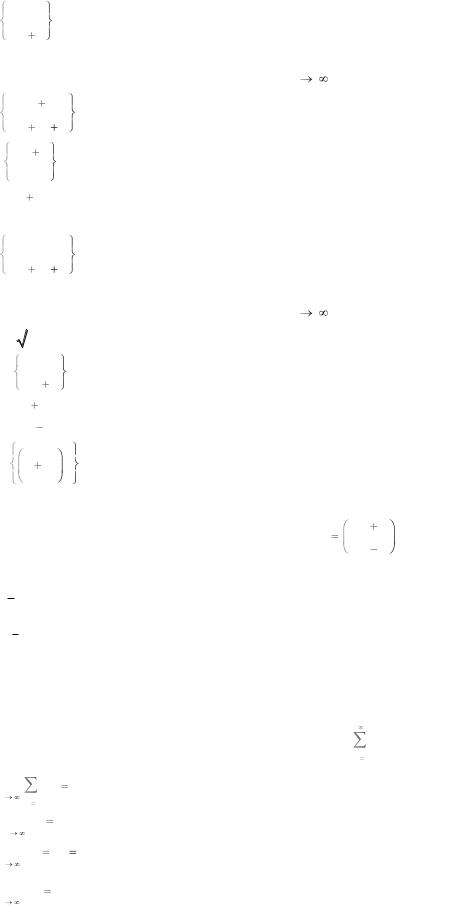
-: |
|
|
2 n 2 |
|
|
|
||||||
|
n |
2 |
|
1 |
|
|
|
|
||||
|
|
|
|
|
|
|
||||||
I: |
|
|
|
|
|
|
|
|
|
|
|
|
S: Наименьшее значение предела при n |
имеет последовательность … |
|||||||||||
-: |
|
|
|
n 2 |
|
|
|
|
2 |
|
|
|
|
n |
2 |
|
|
n |
1 |
|
|
||||
|
|
|
|
|
|
|||||||
+: |
|
|
n 2 |
1 |
|
|
|
|||||
|
|
|
n 3 |
|
|
|
||||||
|
|
|
|
|
|
|
||||||
-: |
2 n |
1 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
n |
|
|
|
|
|
|
|
|
-: |
|
|
|
|
n 3 |
|
|
|
||||
|
n |
2 |
|
|
n |
1 |
|
|
||||
|
|
|
|
|
|
|||||||
I: |
|
|
|
|
|
|
|
|
|
|
|
|
S: Наименьшее значение предела при n |
имеет последовательность … |
|||||||||||
-: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n n |
|
|
|
|
|
|
|
||
+:
-:
|
|
n |
|
|
|
|
|
|
n 2 |
1 |
|
n |
1 |
|
|
|
|
|
|
2 n |
1 |
|
|
|
1 |
n |
|
|
|
||
-: |
|
|
|
|
|||
1 |
|
|
|
|
|
||
n |
|
|
|
|
|||
|
|
|
|
|
|
||
I: |
|
|
|
|
|
|
|
|
|
|
|
3n |
1 |
2 n |
|
S: Предел числовой последовательности a n |
|
|
равен … |
||||
3n |
1 |
||||||
|
|
|
|
|
|||
-: 1 |
|
|
|
|
|
|
|
3
-: e 4
4
+: e 3 -: e 2
V2: Признаки сходимости числовых рядов
I:
S: Необходимым признаком сходимости ряда a n является:
|
n 1 |
n |
|
-: lim |
a n 0 |
n |
|
n 1 |
|
+: lim a n |
0 |
n |
|
-:
-:
I:
lim a n |
C co n st |
||
n |
|
|
|
lim |
1 |
0 |
|
a n |
|||
n |
|
||
|
|
||
8

S: Если для рядов |
a n и |
bn с положительными членами выполняется |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
1 |
|
n 1 |
|
|
|
|
|
неравенство a n bn , то: |
|
|
|
|
|
|
|||||||||||||||
-: из сходимости |
a n |
следует сходимость |
bn |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
|
n 1 |
|
|
|
|
-: из расходимости |
|
bn |
следует расходимость |
a n |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
n 1 |
|
|
+: из сходимости |
bn |
следует сходимость |
a n |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
1 |
|
|
n |
1 |
|
|
|
+: из расходимости |
|
a n |
следует расходимость |
bn |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
|
n 1 |
|
|
|
I: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S: Признак Даламбера сходимости числового ряда |
a n |
с положительными |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
членами a n |
|
|
|
|
|
|
|
|
|||||||||||||
заключается в том, что … |
|
|
|
|
|
||||||||||||||||
-: D |
lim |
a n 1 |
|
, при D |
1 - ряд расходится, при D |
1 - ряд сходится |
|||||||||||||||
|
|
|
|
|
|
||||||||||||||||
|
n |
|
|
|
a n |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
+: D |
lim |
a n 1 |
, при D |
1 - ряд сходится, при D |
1 - ряд расходится |
||||||||||||||||
|
|
|
|
|
|
||||||||||||||||
|
n |
|
|
|
a n |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
-: D |
lim n a n , при D |
1 - ряд расходится, при D |
1 - ряд сходится |
||||||||||||||||||
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
-: D |
lim n a n , при D |
1 - ряд сходится, при D |
1 - ряд расходится |
||||||||||||||||||
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S: Признак Коши сходимости числового ряда |
a n с положительными |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
1 |
|
|
членами a n |
|
|
|
|
|
|
|
|
|||||||||||||
заключается в том, что … |
|
|
|
|
|
||||||||||||||||
-: K |
lim |
a n 1 |
|
, при K |
1 - ряд расходится, при K |
1 - ряд сходится |
|||||||||||||||
|
|
|
|||||||||||||||||||
|
n |
|
|
|
a n |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
-: K |
lim |
a n 1 |
|
, при K |
1 - ряд сходится, при K |
1 - ряд расходится |
|||||||||||||||
|
|
|
|||||||||||||||||||
|
n |
|
|
|
a n |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
||||||||||||||
-: K |
lim n a n , при K |
1 - ряд расходится, при K |
1 - ряд сходится |
||||||||||||||||||
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
+: K |
lim n a n , при K |
1 - ряд сходится, при K |
1 - ряд расходится |
||||||||||||||||||
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S: Интегральный признак сходимости числового ряда |
a n с |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
невозрастающими членами заключается в том, что … |
|
||||||||||||||||||||
-: если |
|
|
|
f ( x ) d x , ãä å |
f ( n ) |
a n |
сходится, то ряд сходится; |
|
|||||||||||||
+: если |
|
|
|
f ( x ) d x , ãä å f ( n ) |
a n |
расходится, то ряд расходится; |
|||||||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9
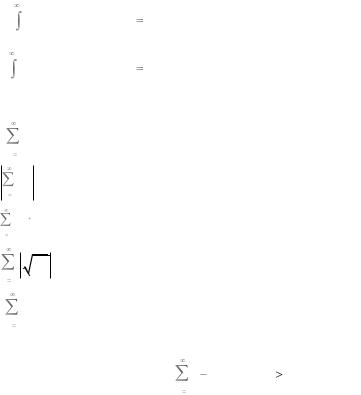
+: если |
|
f ( x ) d x , ãä å |
f ( n ) |
a n |
сходится, то ряд сходится; |
||
|
1 |
|
|
|
|
|
|
-: если |
|
f ( x ) |
d x , ãä å |
f ( n ) |
a |
|
сходится, то ряд сходится; |
|
|
n |
|||||
|
|
a n |
|
|
|
||
1 |
|
|
|
|
|
||
I:
S: Ряд
a n называется абсолютно сходящимся, если
n 1
-: ряд a n сходится
n |
1 |
|
|
|
-: ряд |
|
a n 1 |
|
сходится |
|
|
|||
n 1 |
|
a n |
|
|
-: ряд n  a n сходится
a n сходится
n 1
+: ряд |
|
a n |
|
сходится |
|
|
|||
|
n 1 |
|||
I:
S: Знакочередующийся ряд
( 1) n a n , a n 0 сходится, если
n 1
+: члены ряда монотонно убывают по абсолютной величине и предел их равен нулю -: члены ряда монотонно возрастают по абсолютной величине и предел их равен нулю
-: члены ряда монотонно убывают по абсолютной величине и предел их не равен нулю -: члены ряда монотонно возрастают по абсолютной величине и предел их не равен нулю
I:
S: Необходимый признак сходимости не выполнен для рядов …
-: 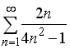 -:
-:  +:
+: 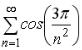
+: 
V2: Сходимость знакоположительных числовых рядов
I:
S: Сходящимися среди приведенных ниже числовых рядов являются …
+: 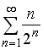
10
