
2012_MATAN-2 / 2012 МАТАН-2 / 2012 ПРАКТИКА / ПРАКТИКА №12-13 Функциональные ряды. Степенные ряды. Ряды Тейлора
..doc
Практическое занятие:
Тема: Функциональные ряды. Степенные ряды. Ряды Тейлора и Маклорена.
Для нахождения
области сходимости ряда
![]() применяют известные признаки сходимости
числовых рядов.
применяют известные признаки сходимости
числовых рядов.
В частности, на
основании признаков Даламбера и Коши
(радикального) можно утверждать, что
ряд сходится (и притом абсолютно), если
![]() и
и
![]() ,
соответственно, и расходится, если
,
соответственно, и расходится, если
![]() .
В точках
.
В точках
![]() ,
в которых
,
в которых
![]() ,
сходимость ряда исследуют с помощью
других признаков (например, признаков
сравнения, интегрального признака Коши,
признака Лейбница) .
,
сходимость ряда исследуют с помощью
других признаков (например, признаков
сравнения, интегрального признака Коши,
признака Лейбница) .
В задачах 8.125-8.139 найти области сходимости следующих функциональных рядов:
8.125
![]() .
8.126
.
8.126
![]() .
8.127
.
8.127
![]() .
8.128
.
8.128
![]() .
8.130
.
8.130
![]() .
.
8.132
![]() .
8.133
.
8.133
![]() .
8.135
.
8.135
![]() .
8.136
.
8.136
![]() .
8.138
.
8.138
![]() .
.
Степенным рядом
называется функциональный ряд вида
![]() ,
где
,
где
![]() -
действительные числа. Числа
-
действительные числа. Числа
![]() называются коэффициентами
ряда. Всякий степенной ряд сходится в
точке
называются коэффициентами
ряда. Всякий степенной ряд сходится в
точке
![]() .
.
Радиусом
сходимости
степенного ряда
![]() называется число
называется число
![]() такое, что при
такое, что при
![]() ряд сходится (и притом абсолютно), а при
ряд сходится (и притом абсолютно), а при
![]() расходится. Интервал
расходится. Интервал
![]() при этом называется интервалом
сходимости
ряда. На концах интервала сходимости,
т.е. в точках
при этом называется интервалом
сходимости
ряда. На концах интервала сходимости,
т.е. в точках
![]() ,
ряд может как сходится, так и расходится.
,
ряд может как сходится, так и расходится.
Областью сходимости
степенного ряда является интервал
сходимости
![]() ,
к которому присоединяются точки
,
к которому присоединяются точки
![]() ,
если в них ряд сходится. В частности,
радиус сходимости
,
если в них ряд сходится. В частности,
радиус сходимости
![]() может быть равен
может быть равен
![]() ,
тогда область сходимости ряда состоит
из одной точки
,
тогда область сходимости ряда состоит
из одной точки
![]() ,
и
,
и
![]() ,
тогда областью сходимости ряда является
вся числовая прямая.
,
тогда областью сходимости ряда является
вся числовая прямая.
Интервал сходимости
![]() определяют
обычно с помощью признаков Даламбера
или Коши (радикального), вычисляя пределы
определяют
обычно с помощью признаков Даламбера
или Коши (радикального), вычисляя пределы
![]() или
или
![]() и решая неравенство
и решая неравенство
![]() .
.
В задачах 8.140-8.160 найти область сходимости следующих степенных рядов:
8.140![]() .
8.141
.
8.141![]() .
8.142
.
8.142![]() .
8.143
.
8.143![]() .
8.144
.
8.144![]() .
8.145
.
8.145![]() .
.
8.146![]() .
8.147
.
8.147![]() .
8.148
.
8.148![]() .
8.149
.
8.149
![]() .
8.150
.
8.150![]() .
.
8.151![]() .
8.154
.
8.154![]() .
8.155
.
8.155![]() .
8.156
.
8.156![]() .
8.160
.
8.160![]() .
.
Внутри общего
интервала сходимости
![]() степенные ряды можно почленно складывать
и вычитать, полученные при этом ряды
имеют тот же интервал сходимости:
степенные ряды можно почленно складывать
и вычитать, полученные при этом ряды
имеют тот же интервал сходимости:
![]() .
.
Внутри интервала
сходимости
![]() степенной ряд можно почленно
дифференцировать и интегрировать,
полученные при этом ряды имеют тот же
интервал сходимости:
степенной ряд можно почленно
дифференцировать и интегрировать,
полученные при этом ряды имеют тот же
интервал сходимости:
1)
![]() ;
2)
;
2)
![]() .
.
Степенной ряд
![]() называется
рядом Тейлора
функции
называется
рядом Тейлора
функции
![]() в точке
в точке
![]() .
При
.
При
![]() ряд Тейлора называется рядом
Маклорена:
ряд Тейлора называется рядом
Маклорена:
![]() .
.
Представление
функции
![]() в виде
в виде
![]() ,
называется разложением
,
называется разложением
![]() в ряд Тейлора.
в ряд Тейлора.
При разложении функций в степенные ряды, как правило, используют основные разложения элементарных функций в ряд Маклорена:
1.
 ,
,
![]() 2.
2.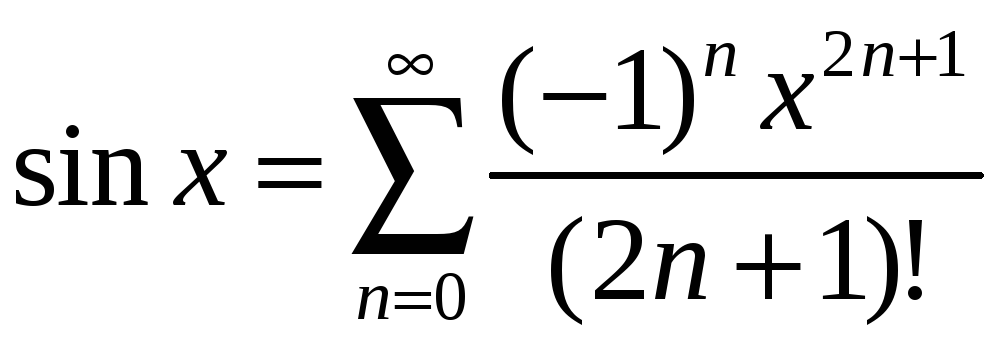 ,
,
![]() 3.
3.
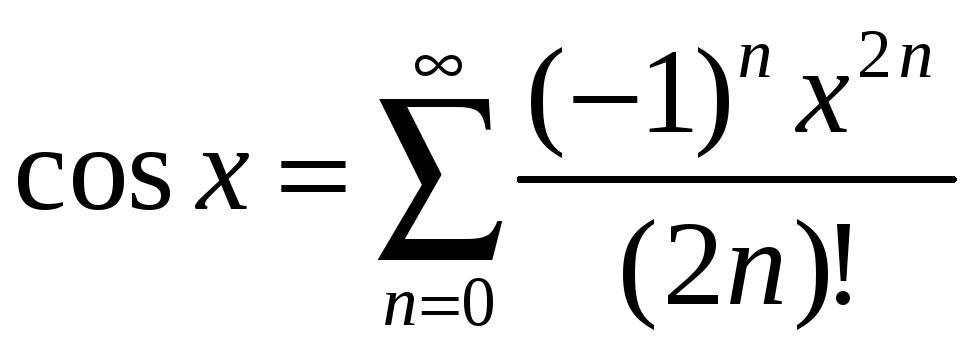 ,
,
![]()
4.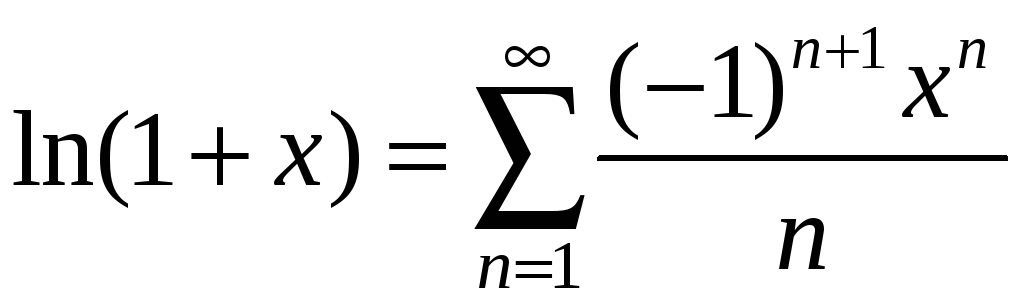 ,
,
![]() 5.
5.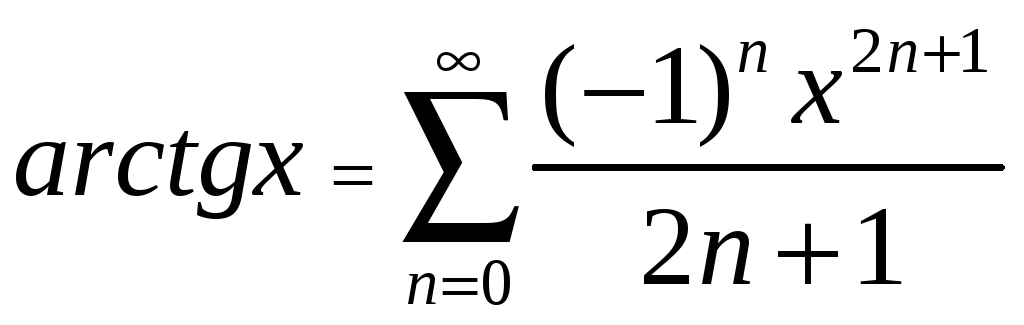 ,
,![]() 6.
6.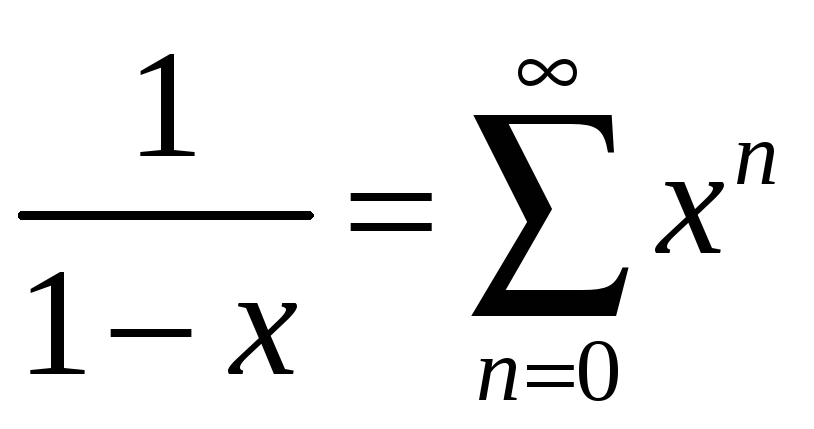 ,
,
![]() 7.
7.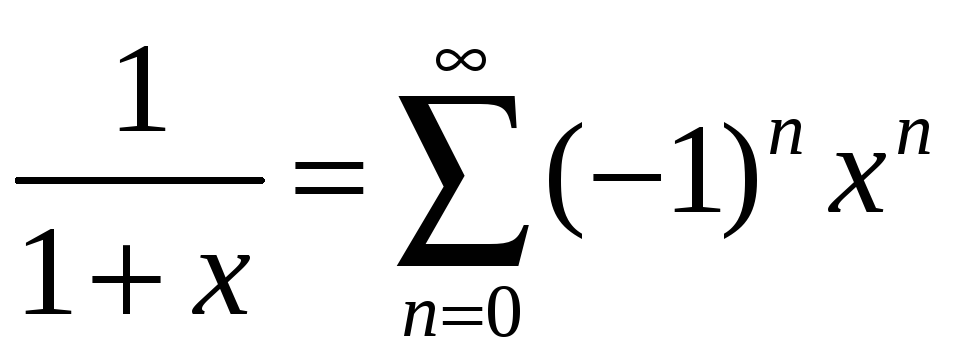 ,
,![]() 8.
8.
![]()
![]() ,
,
![]() ,
,
![]() .
.
Иногда при разложении используют почленное дифференцирование или интегрирование. При разложении в степенные ряды рациональных дробей рекомендуется представлять их в виде суммы простейших дробей.
В задачах 8.161-8.178 используя основные разложения элементарных функций, а также возможность почленного дифференцирования и интегрирования степенных рядов, разложить функции в ряд Маклорена и указать интервалы сходимости полученных рядов.
8.161
![]() .
8.162
.
8.162
![]() .
8.163
.
8.163
![]() .
8.164
.
8.164
![]() .
8.166
.
8.166
![]() .
8.167
.
8.167
![]() .
.
8.168
![]() .
8.169
.
8.169
![]() .
8.170
.
8.170
![]() .
8.173
.
8.173
![]() .
8.175
.
8.175
 .
8.176
.
8.176
 .
.
В задачах
8.179-8.186
вычислить указанные выражения с точностью
![]() .
.
8.179
![]() .
8.180
.
8.180
![]() .
8.181
.
8.181
![]() .
8.182
.
8.182
![]() .
8.183
.
8.183
![]() .
8.184
.
8.184
![]() .
8.185
.
8.185
![]() .
8.186
.
8.186
![]() .
.
В задачах
8.188-8.193
вычислить следующие интегралы с точностью
![]() .
.
8.188
![]() .
8.189
.
8.189
![]() .
8.190
.
8.190
![]() .
8.191
.
8.191
![]() .
8.192
.
8.192
![]() .
.
ОТВЕТЫ:
8.125
![]() 8.126
8.126
![]() 8.127 Расходится.
8.128
8.127 Расходится.
8.128
![]() 8.130
8.130
![]() 8.132
8.132
![]() 8.133
8.133
![]() 8.135
8.135
![]() 8.136
8.136
![]() 8.138
8.138
![]() 8.140
8.140
![]() 8.141
8.141
![]() 8.142
8.142
![]() 8.143
8.143
![]() 8.144
8.144
![]() 8.145
8.145
![]() 8.146
8.146
![]() 8.147
8.147
![]() 8.148
8.148
![]() 8.149
8.149
![]() 8.150
8.150
![]() 8.151
8.151
![]() 8.154
8.154
![]() 8.155
8.155![]() 8.156
8.156
![]() 8.160
8.160
![]() 8.161
8.161![]() 8.162
8.162
![]() 8.163
8.163![]() 8.164
8.164![]() 8.166
8.166
![]() 8.167
8.167
![]() 8.168
8.168
![]() 8.169
8.169
![]() 8.170
8.170![]() 8.173
8.173![]() 8.175
8.175![]() 8.176
8.176![]() 8.179
8.179
![]() 8.180
8.180
![]() 8.181
8.181
![]() 8.182
8.182
![]() 8.183
8.183
![]() 8.184
8.184
![]() 8.185
8.185
![]() 8.186
8.186
![]() 8.188
8.188
![]() 8.189
8.189
![]() 8.190
8.190
![]() 8.191
8.191
![]() 8.192
8.192
![]()
