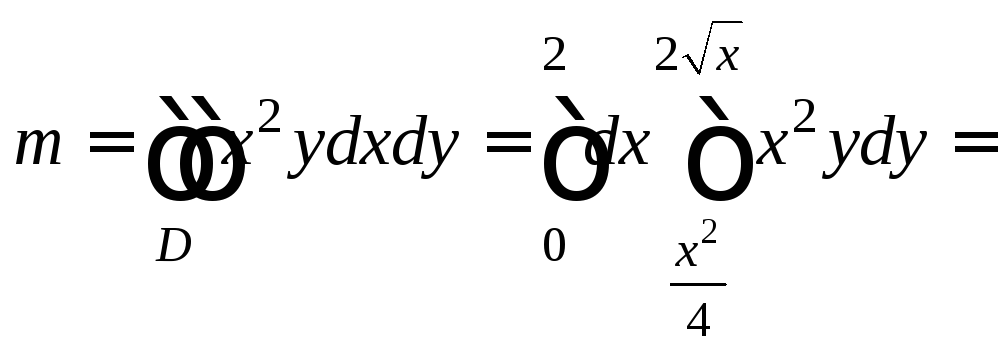I уровень

1.1. Вычислите двойной интеграл по области D, ограниченной указанными линиями, используя полярные координаты:

1)

2)

3)

4)

II уровень

2.1. Вычислите двойной интеграл по области D, ограниченной указанными линиями, используя полярные координаты:

1)

2)

3)

4)

III уровень

3.1. Вычислите двойной интеграл по области D, ограниченной указанными линиями, используя полярные координаты:

1)

2)

3)

4)

5)

24.3. Геометрические и физические приложения

двойных интегралов

1. Площадь плоской фигуры D равна

(24.9)

где первый интеграл вычисляется в декартовой системе координат, а второй – в полярной.

2. Объем v цилиндрического тела V (рис. 24.16), ограниченного сверху поверхностью находят по формуле

(24.10)

где D – основание криволинейного цилиндра, а его образующие параллельны оси Oz.

Рис. 24.16

3. Для нахождения площади ограниченной части поверхности, заданной уравнением и имеющей проекциюна плоскостьxOy, применяют формулу

(24.11)

где и– непрерывные в областифункции.

4. Если f(x; y) – непрерывная функция, выражающая поверхностную плотность распределения массы по плоской пластине D, то масса m этой плоской пластины вычисляется по формуле

(24.12)

5. Для нахождения координат центра масс плоской материаль­ной пластины D c поверхностной плотностью распределения массы, выражаемой функцией f(x; y), применяют следующие формулы:

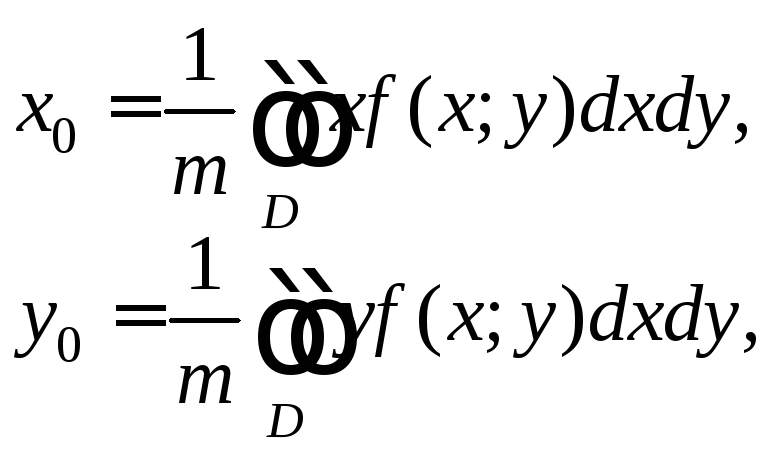(24.13)

где m – масса пластины D, вычисляемая по формуле (24.12).

Пример 1. Найти площадь области D, ограниченной указанными кривыми:

1) 2)

Решение. 1) Изобразим область D (рис. 24.17).

Рис. 24.17

Она является правильной в направлении оси Oy. Найдем точки пересечения двух графиков, чтобы найти проекцию области на ось Ox: Получаем: Найдем границы изменения координат интегрирования: Вычислим площадь области D по формуле (24.9)

2) Изобразим область интегрирования D (рис. 24.18).

Рис. 24.18

Она является правильной в на­правлении оси Oy. Найдем точки пе­ресечения двух графиков, ограничи­вающих область интегрирования, и определим границы изменения коор­динат интегрирования: Вычислим площадь области D по формуле (24.9):

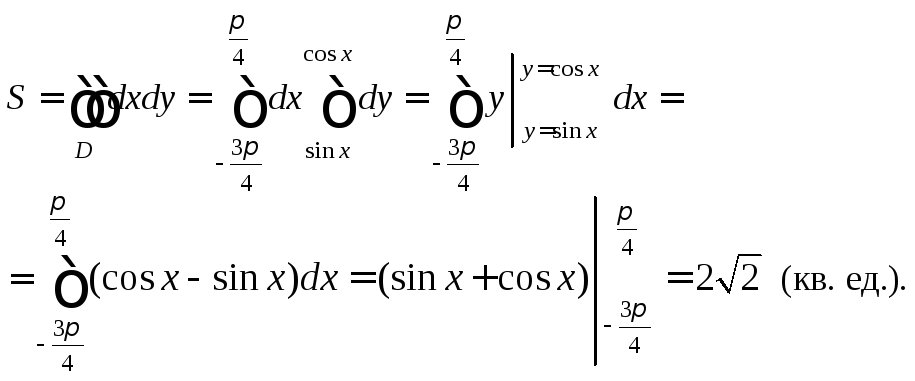
Пример 2. Найти площадь области D, ограниченной указанными кривыми, используя полярные координаты:

1) (трехлепестковая роза);

2) (лемниската Бернулли).

Решение. 1) Изобразим шестую часть области интегрирования D (рис. 24.19).

Рис. 24.19

Используем симметрию заданной области. Определим границы изменения переменных интегрирования (с учетом того, что мы рассматриваем шестую часть искомой площади):

Вычислим площадь области D по формуле (24.9), перейдя к полярным координатам:

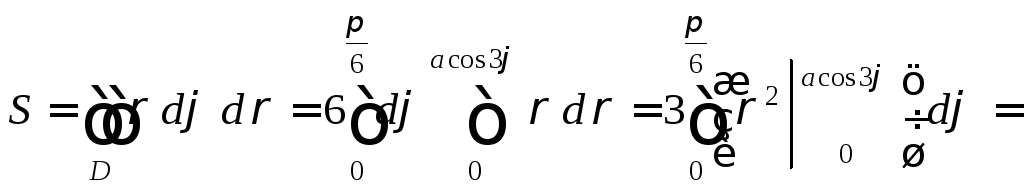
(кв. ед.).

2) Запишем уравнение лемнискаты Бернулли в полярных координатах: откудаОкончательно имеем:

Изобразим четвертую часть области интегрирования D (рис. 24.20).

Рис. 24.20

Используем симметричность об­ласти интегрирования. С учетом того, что мы рассматриваем четвертую часть искомой площади, определим границы изменения переменных интегрирования:

Вычислим площадь области D по формуле (24.9)

Пример 3. Используя двойной интеграл, вычислить объем тела, ограниченного указанными поверхностями:

1)

2)

Решение. 1) Изобразим тело V (рис. 24.21), объем которого необходимо найти, и спроектируем его на плоскость xOy.

При этом мы получим плоскую область (рис. 24.22).

Определим границы интегрирования, исходя из области

Применив формулу (24.10), получим:

Рис. 24.21

Рис. 24.22

2) Найдем пересечение сферы с центром в точке (0; 0; 2) радиуса 2 и кругового параболоида, ограничивающих тело V: Следовательно, Окончательно имеем:

Изобразим указанное тело V (рис. 24.23).

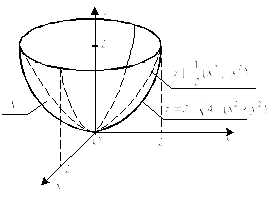
Рис. 24.23

Его проекцией на плоскостьxOy будет являться круг с центром в начале координат радиуса 2. Запишем уравнение окружности ограничивающей область интегрированияв полярных координатах:Используем симметричность областиДля ее четвертой части определим границы интегрирования в полярных координатах:

Выразим подынтегральные функции через полярные координаты, для чего используем формулы перехода (24.4). Получим уравнения: кругового параболоида и сферы

Вычисляем объем тела V по формуле (24.10), представив это тело как разность между двумя криволинейными цилиндрами, один из которых ограничен сверху параболоидом, а другой – сферой:

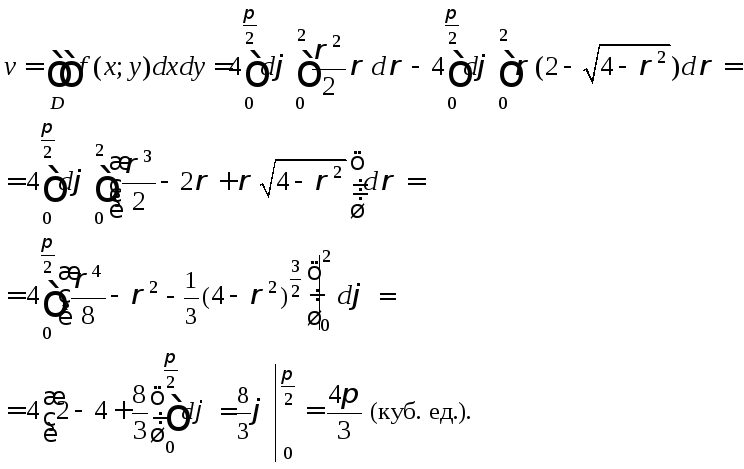
Пример 4. Вычислить площадь поверхности при условии, что .

Решение. Изобразим часть плоскости лежащую в первом октанте, как того требует условие задачи (рис. 24.24).

Вычислим элемент площади по формуле (см. соотношение 24.11).

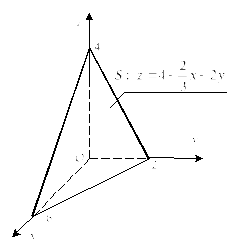
Рис. 24.24

а потому элемент площади будет иметь вид:

Спроектируем поверхность, площадь которой необходимо найти, на одну из координатных плоскостей (в данном случае – на плоскость xOy) и получим плоскую область ограниченную прямыми(рис. 24.25).

Рис. 24.25

Определим границы изменения координат x и y, ориентируясь на область интегрирования . Вычислим искомую площадь поверхности S по формуле (24.11):

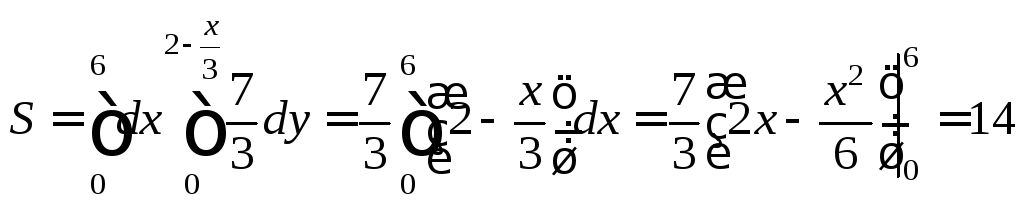(кв. ед.).

Пример 5. Вычислить площадь части кругового параболоида вырезаемого цилиндром

Решение. Изобразим указанную поверхность (рис. 24.26).

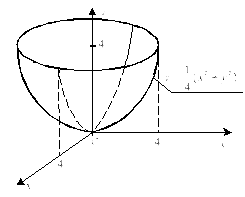
Рис. 24.26

Ее проекцией на плоскость xOy будет круг. Найдем уравнение линии пересечения параболоида и цилиндра, ограничивающей этот круг:

Таким образом, видим, что поверхность проектируется на круг Вычислим значение выраженияиз формулы (24.11).

В нашем случае: Следовательно,Итак, выражение имеет вид:

Вычислим искомую площадь поверхности по формуле (24.11), перейдя в двойном интеграле к полярным координатам по формулам (24.4):

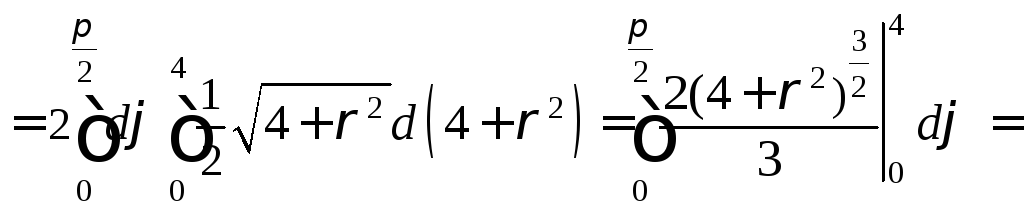
(кв.ед.).

Пример 6. Найти массу плоской пластины D, ограниченной линиями если плотность распределения массы на пластине

Решение. Изобразим пластину D (рис. 24.27).

Рис. 24.27

Расставим пределы интегрирования, исходя из рисунка области D: Найдем массу этой пластины по формуле (24.12):

Пример 7. Найти координаты центра масс плоской однородной пластины D, ограниченной линиями и

Решение. Изобразим пластину D (рис. 24.28).

Рис. 24.28

В уравнениях кривых, ограничивающих указанную область, выразим x через y, поскольку область является элементарной в направлении оси Ox. Из первого уравнения имеем: т. е. Из второго уравнения линии получаем: Определим границы изменения переменной y: Учитывая симметричность отрезка измененияy, будем считать, что

Найдем массу этой пластины по формуле (24.12):

Воспользуемся формулами (24.13) и вычислим сначала абсциссу, а затем и ординату центра масс пластины:

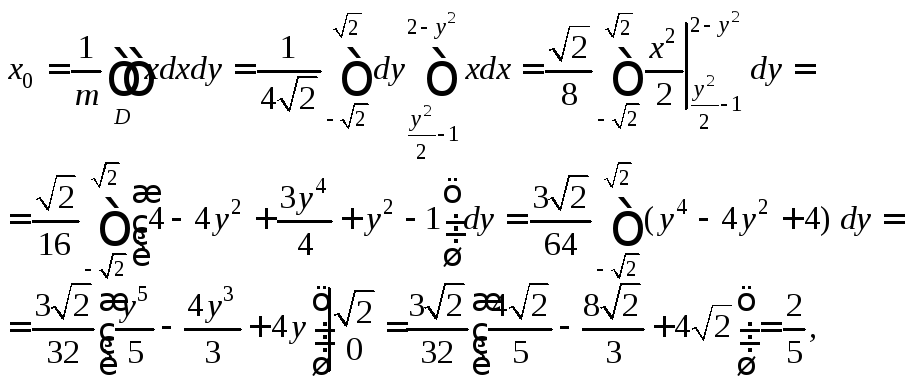
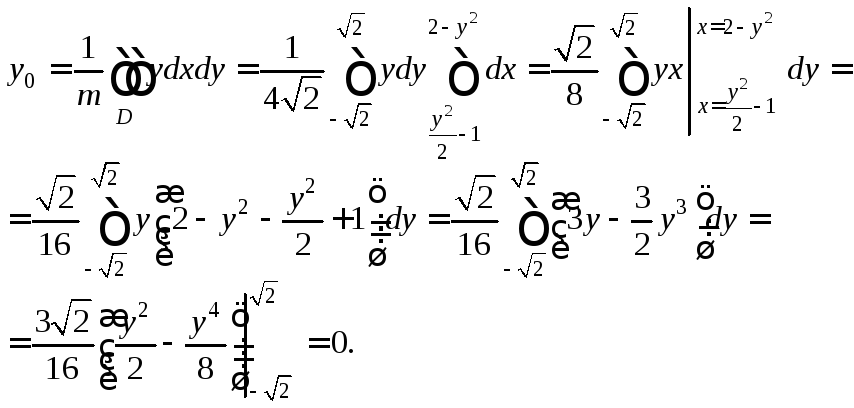
Таким образом, точка – центр масс данной пластины.

Задания