I уровень

1.1.Вычислите площадь фигуры, ограниченной линиями:

1)

2)

3)

4)

5)

1.2.Вычислите объем тела, полученного вращением фигуры, ограниченной данными линиями, вокруг указанных осей координат:

1) вокруг осейOxиOy;

2) вокруг осиOx;

3) вокруг осиOx;

4) вокруг осиOx;

5) вокруг осейOxиOy.

1.3.Вычислите длину дуги кривой:

1) от точкидо точки

2) от точкидо точки

1.4.Скорость движения автобуса задается формулой(м/с). Определите, какой путь пройдет автобус за 10 с от начала движения.

1.5.Найдите, какую работу нужно совершить, чтобы растянуть пружину на 20 см, если сила в 10 Н растягивает пружину на 5 см (упругая сила по закону Гука равна).

1.6.Найдите площадь поверхности вращения, если вращается кривая:

1) дуга синусоиды вокруг осиOx;

2) окружность вокруг полярной оси.

II уровень

2.1.Вычислите площадь фигуры, ограниченной линиями:

1) 2)

3) 4)

5) 6)

7) кардиоидой 8)

9) 10)

11) 12) астроидой

13) эллипсом 14) эллипсом

15) 16)

17) лемнискатой Бернулли

18)

19) одним лепестком трехлепестковой розы

20) одним лепестком четырехлепестковой розы

21) спиралью Архимеда и радиус-векторамии

2.2.Вычислите длину дуги кривой:

1) окружности

2) кардиоиды

3)

4)

5) астроиды

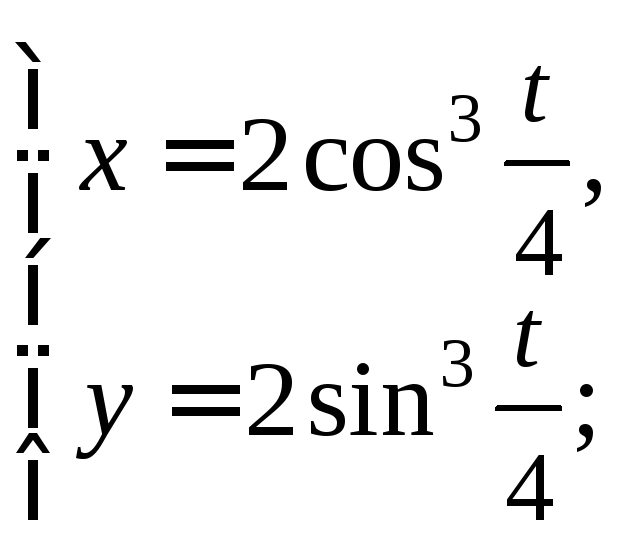
6) эллипса

7) отдо

8) отдо

9) полукубической параболы от точкидо точки

10) от вершины до точки с абсциссой

11) циклоиды

12) от точкидо точки

2.3.Вычислите объем тела, полученного вращением плоской фигуры, ограниченной данными линиями, вокруг указанных осей координат:

1) вокруг осейOxиOy;

2) вокруг осиOy;

3) вокруг осиOx;

4) лемнискаты Бернулли вокруг полярной оси;

5) астроиды вокруг осиOx;

6) одной арки циклоиды вокруг осиOx.

2.4.Найдите объем тела, ограниченного поверхностями:

1) 2)

3)

2.5.Найдите площадь поверхности вращения, если вращается кривая:

1) дуга параболы вокруг осиOx;

2) одна арка циклоиды вокруг осиOy;

3) эллипс вокруг осиOx;

4) дуга линии вокруг оси Ox;

5) астроида вокруг оси Ox;

6) кардиоида вокруг ее оси;

7) кардиоида вокруг полярной оси.

III уровень

3.1.Вычислите площадь фигур, на которые параболаразбивает круг

3.2.Найдите площадь общей части кругаи плоской фигуры, ограниченной кардиоидой

3.3.Найдите площадь фигуры, ограниченной одной аркой циклоидыи прямой

3.4.Найдите длину дуги спирали Архимеданаходящейся внутри окружности

3.5.Найдите объем тела, полученного вращением плоской фигуры, ограниченной линиями:

а) вокруг прямой

б) вокруг прямой

134