
- •20. Определенный интеграл
- •20.1. Понятие определенного интеграла и его свойства
- •I уровень
- •II уровень
- •III уровень
- •20.2. Формула Ньютона-Лейбница. Методы
- •I уровень
- •2. Длина дуги кривой
- •3. Объем тела
- •4. Объем и площадь поверхности тела вращения
- •5. Физические приложения определенного интеграла
- •I уровень
- •II уровень
- •III уровень
I уровень
1.1.Вычислите определенный интеграл, используя формулу Ньютона-Лейбница:
1)
 2)
2)![]() 3)
3)
4)
 5)
5)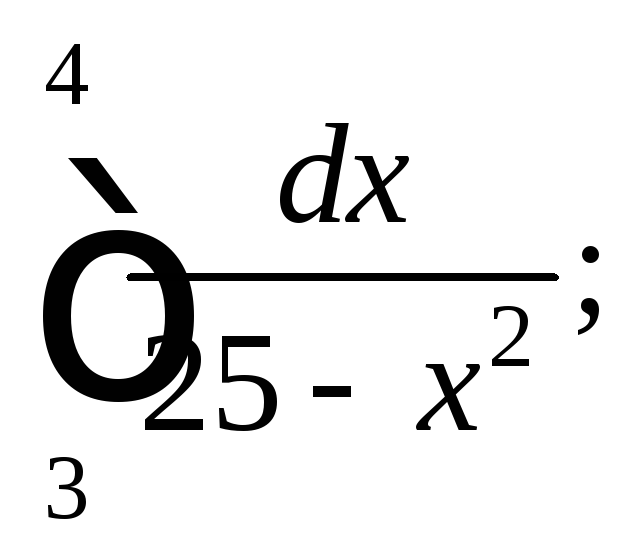 6)
6)
7)
 8)
8) 9)
9)
II уровень
2.1.Вычислите определенный интеграл:
1)
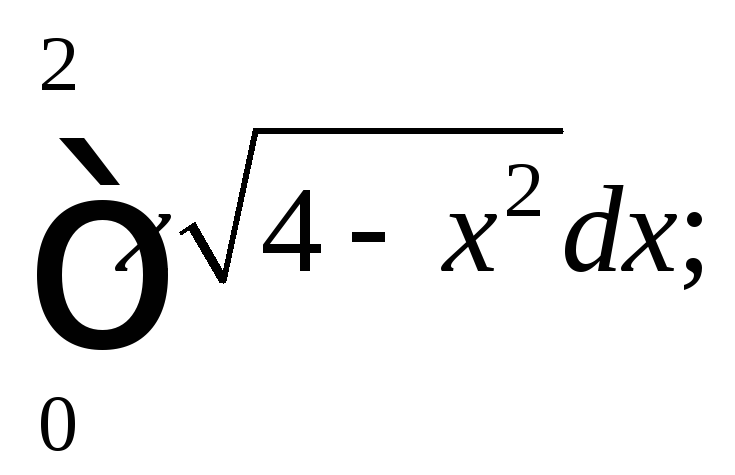 2)
2) 3)
3)
4)
 5)
5)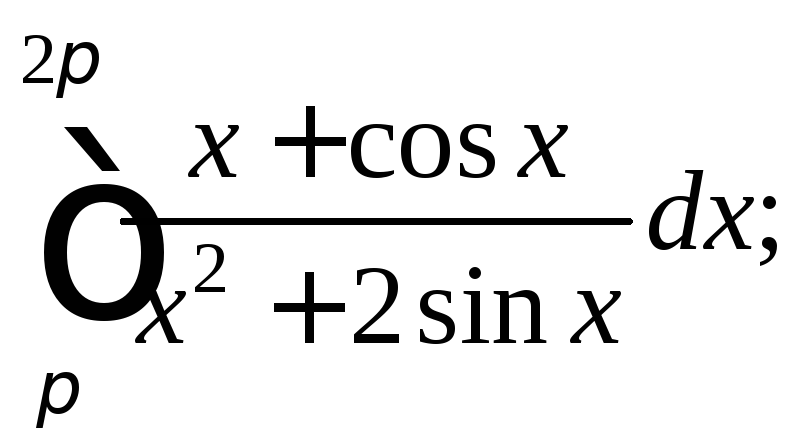 6)
6)
7)
 8)
8) 9)
9)
10)
 11)
11) 12)
12)
2.2.Вычислите определенный интеграл, используя формулу замены переменной:
1)
 2)
2) 3)
3)

4)
 5)
5)
 6)
6)

7)
 8)
8) 9)
9)

2.3.Вычислите определенный интеграл, используя формулу интегрирования по частям:
1)
 2)
2)
3)
 4)
4)
5)
 6)
6)
7)
 8)
8)
9)
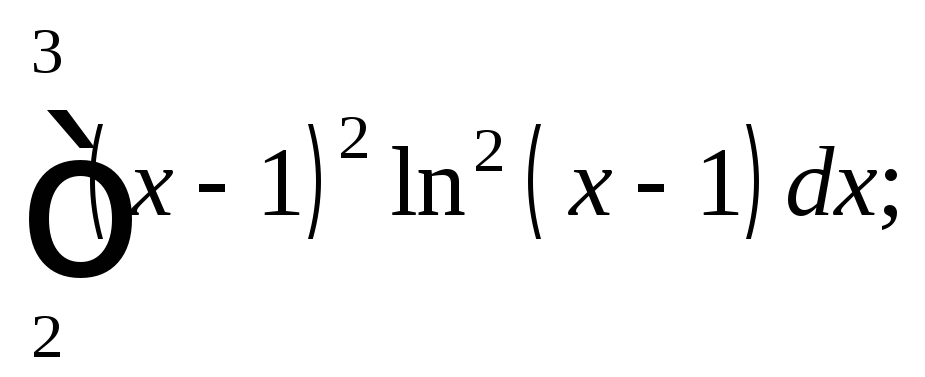 10)
10)
III уровень
3.1.Вычислите определенный интеграл методом замены переменной:
1)
 2)
2)
3)
 4)
4)
5)
 6)
6)
7)
 8)
8)
9)
 10)
10)
11)
 12)
12)
13)
 14)
14)
15)
 16)
16)
17)
 18)
18)
19)

20)

3.2.Вычислите определенный интеграл, используя указанную замену переменной:
1)

![]() 2)
2)
![]()
3)

![]() 4)
4)
![]()
3.3.Вычислите интеграл разными способами:
1)
 2)
2) 3)
3)
20.3. Геометрические и физические приложения
определенного интеграла
1. Площадь плоской фигуры
Площадь криволинейной
трапеции, ограниченной сверху графиком
непрерывной функции
![]()
![]() слева и справа, соответственно, прямыми
слева и справа, соответственно, прямыми![]() и
и![]() снизу – отрезком [a;b] осиOx(рис. 20.3), выражается формулой
снизу – отрезком [a;b] осиOx(рис. 20.3), выражается формулой
 (20.6)
(20.6)
Если
![]() при
при![]() (рис. 20.4), то
(рис. 20.4), то

 (20.7)
(20.7)
Рис. 20.3 Рис. 20.4
Площадь криволинейной
трапеции, ограниченной прямыми
![]()
![]() и кривыми
и кривыми![]()
![]() где
где![]() для
для![]() (рис. 20.5), выражается формулой
(рис. 20.5), выражается формулой
 (20.8)
(20.8)
Площадь криволинейной
трапеции, ограниченной прямыми
![]()
![]() кривой
кривой![]()
![]() и отрезком [c;d]
осиOy(рис. 20.6), выражается
формулой
и отрезком [c;d]
осиOy(рис. 20.6), выражается
формулой
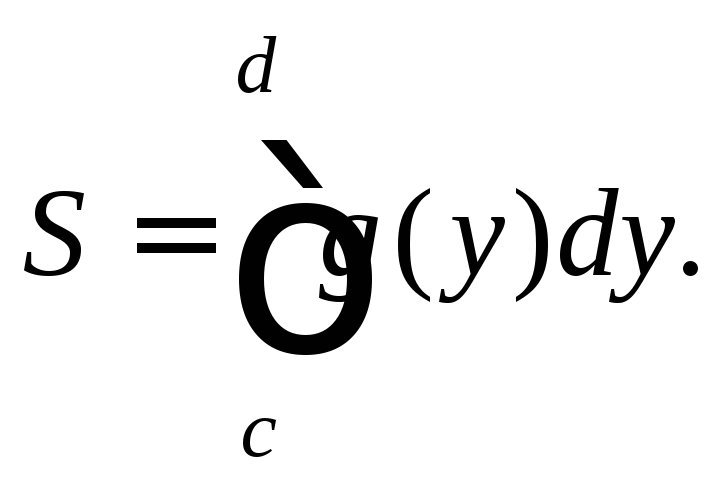 (20.9)
(20.9)

Рис. 20.5 Рис. 20.6
Площадь криволинейной
трапеции, ограниченной прямыми
![]()
![]() и кривыми
и кривыми![]()
![]() где
где![]() для
для![]() (рис. 20.7), выражается формулой
(рис. 20.7), выражается формулой
 (20.10)
(20.10)

Рис. 20.7
Если криволинейная трапеция ограничена сверху кривой, заданной параметрическими уравнениями
![]()
прямыми
![]()
![]() и отрезком [a;b]
осиOx, то ее площадь
вычисляется по формуле
и отрезком [a;b]
осиOx, то ее площадь
вычисляется по формуле
 (20.11)
(20.11)
где
![]() и
и![]() определяются из равенств
определяются из равенств![]()
![]()
Площадь криволинейного
сектора, ограниченного кривой, заданной
в полярных координатах уравнением
![]() и двумя лучами
и двумя лучами![]()
![]()
![]() (рис. 20.8), причем
(рис. 20.8), причем![]() для
для![]() выражается формулой
выражается формулой
 (20.12)
(20.12)
Площадь плоской
фигуры, ограниченной двумя лучами
![]()
![]() и кривыми
и кривыми![]()
![]()
![]() для
для![]() (рис. 20.9), выражается формулой
(рис. 20.9), выражается формулой
 (20.13)
(20.13)

Рис. 20.8 Рис. 20.9
2. Длина дуги кривой
Если функция f (x)
имеет непрерывную производную на отрезке
[a;b],
то длина дуги кривой, заданной уравнением![]() где
где![]() вычисляется по формуле
вычисляется по формуле
 (20.14)
(20.14)
Если кривая задана
уравнением
![]() на отрезке [c; d]
и функция
на отрезке [c; d]
и функция![]() имеет непрерывную производную для
имеет непрерывную производную для![]() то длина дуги определяется по формуле
то длина дуги определяется по формуле
 (20.15)
(20.15)
Если кривая задана
параметрически на плоскости xOyуравнениями![]()
где
![]() и
и![]() – дифференцируемые функции на
– дифференцируемые функции на![]() причем
причем![]() и
и![]()
![]() то длина дуги этой кривой, заключенной
между двумя точками с абсциссами
то длина дуги этой кривой, заключенной
между двумя точками с абсциссами![]() и
и![]() вычисляется по формуле
вычисляется по формуле
 (20.16)
(20.16)
Если кривая задана
в пространстве параметрическими
уравнениями

где
![]()
![]()
![]() – непрерывно дифференцируемые функции
на отрезке
– непрерывно дифференцируемые функции
на отрезке![]() то длина дуги кривой вычисляется по
формуле
то длина дуги кривой вычисляется по
формуле
 (20.17)
(20.17)
Если кривая задана
уравнением
![]()
![]() в полярной системе координат, где
в полярной системе координат, где![]() – функция, которая имеет непрерывную
производную при
– функция, которая имеет непрерывную
производную при![]() то длина дуги вычисляется по формуле
то длина дуги вычисляется по формуле
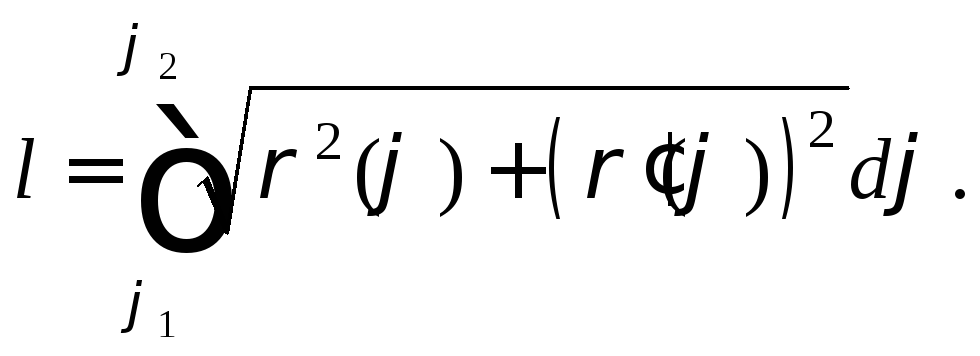 (20.18)
(20.18)
3. Объем тела
Если известна
площадь S(x)
сечения тела плоскостью, перпендикулярной
к осиOx, причемS(x)
является непрерывной функцией на отрезке
[a;b],
то объем тела, заключенного между
плоскостями![]() и
и![]() перпендикулярными к осиOx(рис. 20.10), вычисляется по формуле
перпендикулярными к осиOx(рис. 20.10), вычисляется по формуле
 (20.19)
(20.19)

Рис. 20.10
